
- •Программа дисциплины
- •Раздел 1. Введение. Функции одной переменной
- •Раздел 2. Теория пределов
- •Раздел 3. Непрерывные функции
- •Раздел 4. Производная функции одной переменной
- •Раздел 5. Теоремы дифференциального вычисления. Исследование функций и построение графиков
- •Раздел 6. Функции нескольких переменных
- •Раздел 7. Неопределенный интеграл
- •Раздел 8. Определённый интеграл
- •Раздел 9. Ряды
- •Раздел 10. Дифференциальные уравнения
- •Контрольные задания, правила выполнения и оформления контрольных работ
- •Методические указания Предел функции
- •Производная и дифференциал
- •Общая схема исследования функции и построения графика
- •Применение понятия производной в экономике. Эластичность функции
- •Интегралы
- •Дифференциальные уравнения Решение дифференциальных уравнений 1-го порядка
- •Решение однородного линейного дифференциального уравнение 2-го порядка с постоянными коэффициентами
- •Решение неоднородного линейного уравнения 2-го порядка с постоянными коэффициентами
- •Числовые и степенные ряды
- •Признаки сходимости числового ряда
- •Достаточные признаки сходимости числового ряда с положительными членами
- •Знакочередующиеся ряды.
- •Степенные ряды
- •Задания для выполнения контрольной работы
Методические указания Предел функции
Пусть
функция
![]() ƒ(x)
задана в некоторой окрестности точки
х0.
ƒ(x)
задана в некоторой окрестности точки
х0.
Определение.
Число А называется пределом функции
f(x) в точке х0
если для любого, сколь угодно малого
положительного числа
![]() найдётся такое положительное число
δ>0, зависящее от ε, что для всех х,
удовлетворяющих условию 0<
найдётся такое положительное число
δ>0, зависящее от ε, что для всех х,
удовлетворяющих условию 0<![]() ,
выполняется неравенство
,
выполняется неравенство![]() .
Этот предел функции обозначается:
.
Этот предел функции обозначается:
 или ƒ(х)→А при х→х0.
или ƒ(х)→А при х→х0.
Практическое вычисление пределов основывается на следующих теоремах:
если
существуют
![]() и
и![]() ,
то
,
то
1)
![]() ;
;
2)
![]() ;
;
3)
![]() ;
;
4)
 (при
(при![]() ).
).
Определение.
Функция α (х) называется бесконечно
малой величиной при х→х0,
или при х→∞, если её предел равен нулю

Определение.
Функция
ƒ(х) называется бесконечно большой в
точке х0
(или при х→х0),
если имеет место одно из равенств:

 .
.
Теорема
( о связи бесконечно большой и бесконечно
малой функций) : если
ƒ(х) ─ бесконечно малая функция при
х→х0,
то
![]() ─
бесконечно большая функция при х→х0,
и наоборот.
─
бесконечно большая функция при х→х0,
и наоборот.
Первый
замечательный предел
![]() .
.
Второй
замечательный предел
![]() .
.
Пример
1
![]()
Поскольку функция непрерывна в точке х=7, искомый предел равен значению функции в этой точке. Используя теоремы о пределах суммы, разности, частного, получим
![]() .
.
Пример 2
![]()
При х→5 числитель
(2х + 5) стремится к 2 ∙ 5 + 5 = 15 (т.е. является
ограниченной функцией), а знаменатель
(х – 5) – к нулю (т.е. является бесконечно
малой величиной), очевидно, их отношение
есть величина бесконечно большая, т.е.
![]() .
.
В
рассмотренных примерах предел находился
сразу, чаще при вычислении пределов мы
сталкиваемся с неопределённостями:
![]() ,
,
![]() ,
,
![]() ,
,
![]() .
.
Пример 3

Пример 4

Пример 5
![]() .
.
Теорему о пределе
частного
здесь применить нельзя, так как числитель
и знаменатель дроби конечного предела
не имеют. В данном случае имеем
неопределённость
вида
![]() .
Разделим числитель и знаменатель дроби
на х в высшей степени
(в
данном случае на х2
),
а затем воспользуемся теоремами о
пределах функций:
.
Разделим числитель и знаменатель дроби
на х в высшей степени
(в
данном случае на х2
),
а затем воспользуемся теоремами о
пределах функций:
 .
.
Здесь мы
воспользовались теоремой о
связи бесконечно большой и бесконечно
малой функций
:
![]() (a
– любое число).
(a
– любое число).
Производная и дифференциал
Пусть
функция у
= f(x)
определена на промежутке X. Возьмём
точку х![]() Х.
Дадим значению х приращение
Х.
Дадим значению х приращение
![]() ,
тогда функция получит
приращение
,
тогда функция получит
приращение
![]() .
.
Производной функции у = f(x) называется предел отношения приращения функции к приращению переменной х, при стремлении последнего к нулю (если этот предел существует):
![]() .
.
Основные правила дифференцирования
Если
С
─ постоянное число,
![]() ─ функции, имеющие
производные,
тогда:
─ функции, имеющие
производные,
тогда:
![]() ;
(I)
;
(I)
![]() ;
;![]() (II)
(II)
![]() ; (III)
; (III)
![]() ;
(IV)
;
(IV)
![]() . (V)
. (V)
Если
у
= f(u), u
= φ (х)
─ дифференцируемые функции от своих
аргументов, то производная сложной
функции y=f[(φ(x)]
существует и равна произведению
производной данной функции по
промежуточному аргументу на производную
этого аргумента по независимой переменной
х,
т.е.
![]() (VI).
(VI).
Таблица производных основных функций
|
№ |
Формула |
|
Формула |
|
1 |
|
15 |
|
|
2 |
|
16 |
|
|
3 |
|
17 |
|
|
4 |
|
18 |
|
|
5 |
|
19 |
|
|
6 |
|
20 |
|
|
7 |
|
21 |
|
|
9 |
|
22 |
|
|
10 |
|
23 |
|
|
11 |
|
24 |
|
|
12 |
|
25 |
|
|
13 |
|
26 |
|
|
14 |
|
27 |
|
Пример 6 Найти производные функций:
a)
![]() ;
b)
;
b)![]() ;
c)
;
c)![]() .
.
Решение:
а)
функцию
![]() можно представить в виде
можно представить в виде
![]() ,
где
,
где
![]() ,
воспользуемся правилом дифференцирования
(VI) и формулами таблицы производных
,
воспользуемся правилом дифференцирования
(VI) и формулами таблицы производных
![]() ;
;
b) функция
![]() представлена произведением двух
функций, на основании правила (IV)
представлена произведением двух
функций, на основании правила (IV)
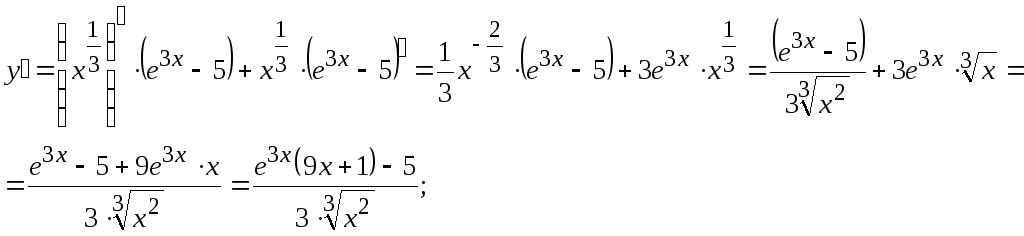
c)
функцию
![]() можно
представить в виде
можно
представить в виде![]() ,
,
где
![]() ,
используя формулы таблицы производных
и правила дифференцирования (V) и
(VI) получим:
,
используя формулы таблицы производных
и правила дифференцирования (V) и
(VI) получим:
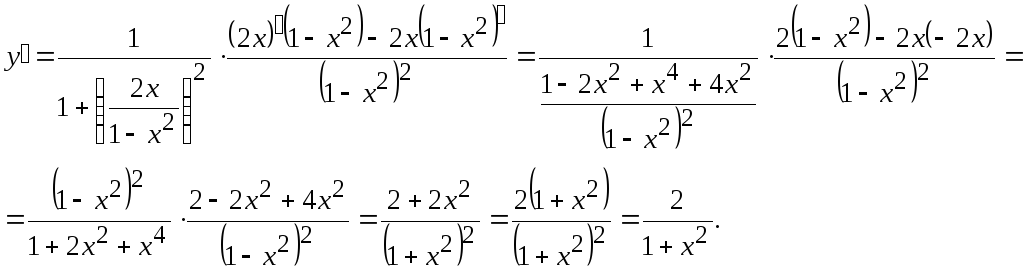
Определение.
Дифференциалом функции у=f(x) называется
главная, линейная относительно
![]()
![]() часть приращения функции, равная
произведению производной на приращение
независимой переменной:
часть приращения функции, равная
произведению производной на приращение
независимой переменной:
![]() .
.
Дифференциал
независимой переменной равен приращению
этой переменной, т.е.
![]() .
Итак, дифференциал функции равен
произведению
её производной на дифференциал
аргумента:
.
Итак, дифференциал функции равен
произведению
её производной на дифференциал
аргумента:![]() .
.
Для определения полного дифференциала функции Z=f(x,y) необходимо ввести понятие частной производной нескольких переменных.
Определение.
Величина
![]() называется полным приращением функции
в точке(х,
у).
Если задать только приращение аргумента
называется полным приращением функции
в точке(х,
у).
Если задать только приращение аргумента
![]() или только приращения аргумента
или только приращения аргумента![]() ,
то полученные приращения функции
соответственно:
,
то полученные приращения функции
соответственно:![]() и
и![]() называются
частными.
называются
частными.
Определение.
Частной
производной от функции
![]() по независимой переменной
по независимой переменной![]() называется конечный предел
называется конечный предел![]() ,вычисленный
при постоянном
,вычисленный
при постоянном
![]() .
.
Определение.
Частной производной от функции
![]() по
по![]() называется конечный предел
называется конечный предел![]() ,вычисленный
при постоянном
,вычисленный
при постоянном
![]() .
.
Обозначается
частная производная так:
![]() или
или
![]()
![]() .
.
Пример 7 Найти частные производные функций:
a)
![]() ;
b)
;
b)
![]()
Решение:
а)
при нахождении частной производной
по х
будем рассматривать
![]() как величину постоянную. Получим:
как величину постоянную. Получим:![]() .
.
Аналогично,
дифференцируя по у,
считаем
![]() постоянной
величиной, т.е.
постоянной
величиной, т.е.
![]() .
.
b) при
фиксированном
![]() имеем степенную функцию отх,
таким образом,
имеем степенную функцию отх,
таким образом,
![]() ;
;
при
фиксированном
![]() функция является показательной
относительно
функция является показательной
относительно![]() ,
тогда
,
тогда
![]() .
.
Полный
дифференциал функции
![]() вычисляется по формуле
вычисляется по формуле
![]() .
.
Пример 8
Найти полный дифференциал функции
![]() .
.
Решение:
![]() ;
;![]() ;
;![]() .
.
