
- •Министерство образования Российской Федерации
- •Дойхен Людмила Архиповна
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
- •Вариант 21
- •Вариант 22
- •Вариант 23
- •Вариант 24
- •Вариант 25
- •Вариант 26
- •Вариант 27
- •Вариант 29
- •Вариант 30
- •Вариант 1
- •Вариант 2
- •Вариант 3
- •Вариант 4
- •Вариант 5
- •Вариант 6
Вариант 29
1.![]() ;
9.
;
9. ;
;
2.![]() ;
10.
;
10.![]() ;
;
3.![]() ;
11.
;
11.![]() ;
;
4.![]() ;
12.
;
12.![]() ;
;
5.![]() ;
13.
;
13. ;
;
6.![]() ;
14.
;
14. ;
;
7.![]() ;
15.
;
15.![]() ;
;
8.![]() ;
16.
;
16.![]() .
.
Найти площадь фигуры, ограниченной линиями :
а)
у=![]() ,у=2-х,
у=0;
,у=2-х,
у=0;
б) у=х2-2х+3,у=3х-1;
в)
у=![]() ,у=-
,у=-![]() .
.
Известно, что существует некоторая зависимость между ценой на бензин на бензоколонке и количеством машин, обслуженных этой бензоколонкой. Определить количество машин, обслуженных бензоколонкой за 30 дней, если изменение цены в течение месяца определялось следующей функцией:
x(t)=3,1
+ 1,2 sin(![]() ).
).
Вариант 30
1.![]() ;
9.
;
9. ;
;
2.![]() ;
10.
;
10.![]() ;
;
3.![]() ;
11.
;
11.
![]() ;
;
4.![]() ;
12.
;
12.![]() ;
;
5.![]() ; 13.
; 13. ;
;
6.![]() ;
14.
;
14. ;
;
7.![]() ;
15.
;
15.![]() ;
;
8.![]() ;
16.
;
16.![]() .
.
17. Найти площадь фигуры, ограниченной линиями :
а)
у=![]() ,
у=х, у=2;
,
у=х, у=2;
б)
у=х2,
у= 1+![]() х2;
х2;
в) у=x2+2,у=1-х2,х=0,х=1.
18.
Известно, что спрос на валюту резко
возрастает с ростом её курса, а затем
падает . Пусть рост курса доллара подчинён
следующему закону: у(t)=![]() ,
гдеt
означает день месяца.Определить
количество валюты, купленной за первые
10 дней месяца.
,
гдеt
означает день месяца.Определить
количество валюты, купленной за первые
10 дней месяца.
Вариант 1
 ;
9.
;
9.
 ;
;
 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Вычислить площадь фигуры, ограниченной линиями:
а) y=x3, y=8, x=0;
б) y=6x-x2, 2x-y+3=0;
в) xy=2, y=x, x=4.
18. Определить дневную выработку рабочего за семичасовой рабочий день, если производительность труда в течение дня изменяется по закону
 y
= 10+2t,
если 0t4
y
= 10+2t,
если 0t4
-x2+8x+2, если 4t7
На сколько процентов дневная выработка оказалась бы больше, если работа велась бы с максимальной производительностью?
Вариант 2
 ;
9.
;
9.
 ;
;
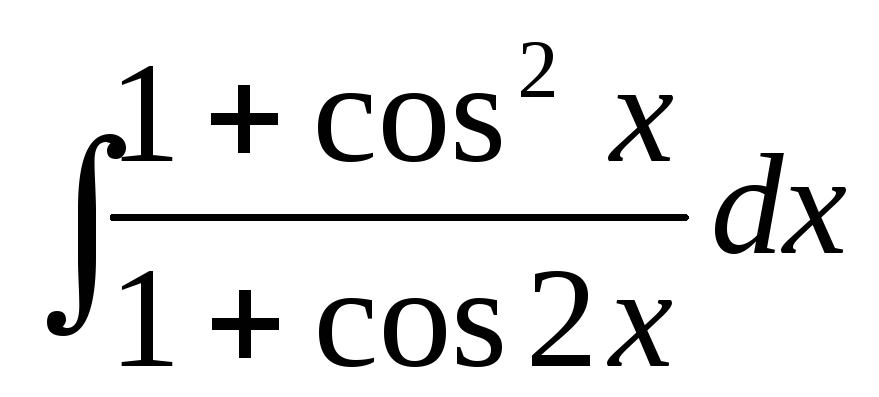 ;
10.
;
10.
 ;
;
 ;
11.
;
11.
 ;
;
 ;
12.
;
12.
 ;
;
 ;
13.
;
13.
 ;
;
 ;
14.
;
14.
 ;
;
 ;
15.
;
15.
 ;
;
 ;
16.
;
16.
 .
.
Найти площадь фигуры, ограниченной линиями:
а) y=x2+1, y=0;
б)
y=![]() ,
y=
,
y=![]() ;
;
в)
y=![]() ,
x=1
и осью OX
,
x=1
и осью OX
18. Уровень ежегодного производства некоторого товара растёт с темпом роста k и определяется функций y= y0ekt, где y0 – уровень в начальный момент (t=0).
Определить суммарное количество товара, произведённое к моменту времени t. Если темп роста составляет 5% ежегодно, то чему равен объём товара через 5 лет?
