9.Формула полной вероятности и формула Байеса

Рассм некот случ событие А. Оно может произойти пи выполнении одной из гипотез. Указанные события образуют полную группу событий, т.е. сумма событий равна достоверному событию и произойдет только одно событие. Известны вер-ти наступления каждой из гипотезP(H1),P(H2),…,P(Hn). Также известны вер-ти наступления события А при вып каждой из гипотез (P(A/H1))… Тогда вероятность наступления события А вычисляется по формуле полной вероятности:

Р{A}=P{A|H1}P{H1}+ P{A|H2}P{H2}+…+ P{A|Hn}P{Hn}= P{A|Hi}P{Hi}

Из формулы полной вероятности следует формула Байеса. Теорема Байеса (или формула Байеса) — одна из основных теорем теории вероятностей, которая позволяет переоценить вероятности \ гипотез после того, как становится известным результат испытания, в итоге которого произошло событие А. Ключевым словосочетанием для прим ф.Байеса явл «событие произошло». [задача про цех]

10.Повторные независимые испытания. Ф-ла Бернулли.

Имеется серия из n повторных независимых испытаний. В каждом из испытаний событие А может произойти (успех), а может не произойти (неуспех). Предполагается, что вер-ть успеха наступления события в каждом испытании постоянна и равна р. Тогда вер-ть наступл неуспеха равна q=1-р. Нас интересует событие, что в серии из n испытаний произойдет ровно k успехов. Эта вер-ть обозначается P_n(k) и вычисляя по ф. Бернулли:

Pn(k)=

11. Наивероятнейшее число появлений события в схеме Бернулли.

Биномиальное распределение (распределение по схеме Бернулли) позволяет, в частности, установить, какое число появлений события А наиболее вероятно. Формула для наиболее вероятного числа успехов (появлений события) имеет вид:

Так как , то эти границы отличаются на 1. Поэтому k , являющееся целым числом, может принимать либо одно значение, когда np целое число (k=np) , то есть когда np+p (а отсюда и np-q) нецелое число, либо два значения, когда np-q целое число.

Вопрос 12. Локальная и интегральная теоремы Лапласа.

Когда n велико, а р мало, то вычисления по формуле Бернулли крайне затруднительны. Поэтому для вычисления вер-тей применяются приближенные формулы, кот. называются ассимптотическим. одной из таких формул явл. формулы Лапласа.

Пусть в каждом из n независимых испытаний событие A может произойти с вероятностью p,q=1-p (условия схемы Бернулли). Обозначим через P­_n(k) вероятность ровно k появлений события А в испытаниях. кроме того, пусть – вероятность того, что число появлений события А находится междуk₁ и k₂ .

Локальная теорема Лапласа.

Если n – велико, а р – отлично от 0 и 1, то вер-ть P_n(k) того, что событие А появится в n испытаниях ровно k раз, приближенно равна значению ф-ии:

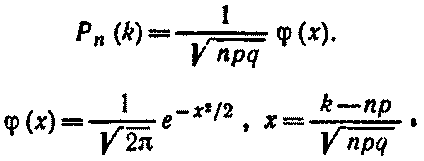
Значения ф-ии фи(х) для положительных х приведены в специальных таблицах. Для отрицательных значений аргумента исп. те же таблицы, т.к. ф-ия фи(х) четная. (фи от –х= фи от х)

Интегральная теорема:

Для того, чтобы посчитать вер-ть наступления не более чем m успехов, когда n велико, прим интегральную теорему Лапласа: =

Замечание:ф-ия для Ф=2/2корня из пи...(в таблице). При Ф=1/2корня из пи.. 1/2 перед формулой убирается.

Осн. св-ва ф-ии Лапласа:

1.Ф(0)=0

2.Ф()=0,5

3.Ф(-t)=-Ф(t)

Для ф-ии Лапласа также есть таблицы ее значений. В таблице даются значения для . Для отр. знач.t исп св-во нечетности ф-ии, т.е. Ф(-t)=-Ф(t)

Если t5, то Ф(t)=0,5 , для любого t5.

Теоремы Лапласа дают удовлетворительное приближение при np>=10. Чем ближе значения p к 0,5, тем точнее данные формулы. При маленьких или больших значениях вероятности (близких к 0 или 1) формула дает большую погрешность (по сравнению с исходной формулой Бернулли).