3.2. Показатели точности прогноза

Любой прогноз несет на себе определенную степень ошибки, поэтому при проведении прогнозов исследователь всегда имеет дело со случайными отклонениями прогнозных значений от их реальных будущих значений. Такие отклонения, как было отмечено, предполагаются распределенными нормально, а мерой их рассеяния служат различные показатели точности прогноза.

Рассмотрим некоторые из них. Пусть y_t– измеренные значения показателей временного ряда, а f_t– прогнозные. Тогда ошибка прогноза за период времени t составит

e_t=y_t–f_t.

Средняя ошибкапрогноза (МЕ) определяется из соотношения

и характеризует степень смещенности прогноза. В идеальном случае МЕ 0. Если прогнозные значения в среднем завышены, то МЕ < 0, если занижены, то МЕ > 0.

Средний квадрат ошибкипрогноза (MSE) определяется из соотношения

.

Средняя абсолютная ошибка(МАЕ) вычисляется из соотношения

.

MSEи МАЕ используются для сравнения процедур прогноза и подбора параметров сглаживания.

Средняя абсолютная процентная ошибка(МРАЕ) вычисляется из соотношения:

и используется для оценки качества прогноза.

Если МРАЕ < 10 %, то точность прогноза высокая, при 10 % < МРАЕ < 20 % –хорошая, если 20 % < МРАЕ < 50 %, то точность прогноза удовлетворительная и при МРАЕ > 50 % – неудовлетворительная. МРАЕ вычисляется по ошибке прогноза на шаг вперед.

Средняя процентная ошибка(МРЕ) вычисляется из соотношения

и служит показателем смещенности прогноза (не должна превышать 5 %).

Кроме того, в некоторых статистических ППП корень квадратный из MSEназывается стандартной ошибкой и обозначаетсяRMSE.

Из разработанных и используемых в практике методов анализа временных рядов рассмотрим лишь несколько наиболее простых, часто используемых на практике и теоретически обоснованных.

Как уже отмечалось, для стационарных и нестационарных временных рядов обычно применяются разные методы анализа. Поэтому в первую очередь ставится задача определения наличия или отсутствия тенденции в элементах временного ряда. Тенденцию можно определять визуально, построив горизонтальный график ряда. Но тенденция проявляется не всегда отчетливо. Поэтому для выявления тренда обычно используются статистические критерии, основанные на проверке статистических гипотез. Рассмотрим один из них, наиболее простой и часто используемый.

3.3. Анализ автокорреляций

Для определения существования зависимости может быть использован метод анализа автокорреляции.

Корреляция, как известно, измеряет степень тесноты линейной связи между двумя различными переменными. Автокорреляция измеряет степень такой же зависимости внутри самой переменной, т. е. “зависимость внутри переменной самой от себя”. Измеряется автокорреляция путем сопоставления фактического ряда данных с тем же рядом, но сдвинутым на некоторый промежуток времени с дальнейшим вычислением коэффициента корреляции между полученными рядами. Величина сдвига при этом называется лагом. Зависимость коэффициентов автокорреляции от величины лага называется автокорреляционной функцией, а график такой зависимости – коррелограммой.

Коэффициенты автокорреляции вычисляются по аналогии с линейным коэффициентом корреляции и поэтому характеризуют тесноту только линейной связи исходных и сдвинутых уровней ряда. По коэффициенту автокорреляции можно судить о наличии только линейной связи между уровнями ряда.

Для стационарных временных рядов закономерность в изменении значений коэффициентов автокорреляции для различных лагов отсутствует, а сами коэффициенты, как правило, незначимы (см. рис. 49 и 50).

Рис. 49. Пример горизонтального графика для стационарного ряда

Рис. 50. Коррелограмма для стационарного временного ряда

Как видим (рис. 50), для стационарных временных рядов все коэффициенты автокорреляции незначимы (не выходят за пределы доверительной области нуля).

При наличии тренда коэффициенты автокорреляции в среднем уменьшаются с увеличением лага, а максимальное значение соответствует лагу, равному единице (см. рис. 51 и 52). При этом несколько первых коэффициентов значимо отличаются от нуля (выходят за пределы доверительной области нуля).

Рис. 51. Пример горизонтального графика для временного ряда с трендом

Рис. 52. Коррелограмма для временного ряда с трендом

Известно, что анализ автокорреляции первых разностей для ряда с линейным трендом обычно показывает их стационарность.

При сезонной составляющей максимальное значение коэффициента автокорреляции наблюдается при лаге, кратном величине сезонности (4 – при квартальных данных и 12 – при помесячных).

Например, для следующего временного ряда (рис. 53) явно прослеживается сезонная составляющая с длиной сезонности, равной 4.

Рис. 53. Пример горизонтального графика временного ряда с сезонной составляющей и трендом

Это и отражено в коррелограмме (рис. 54). Здесь наибольший коэффициент автокорреляции наблюдается при лаге, равном 4. Наличие тренда отражено значительным коэффициентом автокорреляции первого порядка.

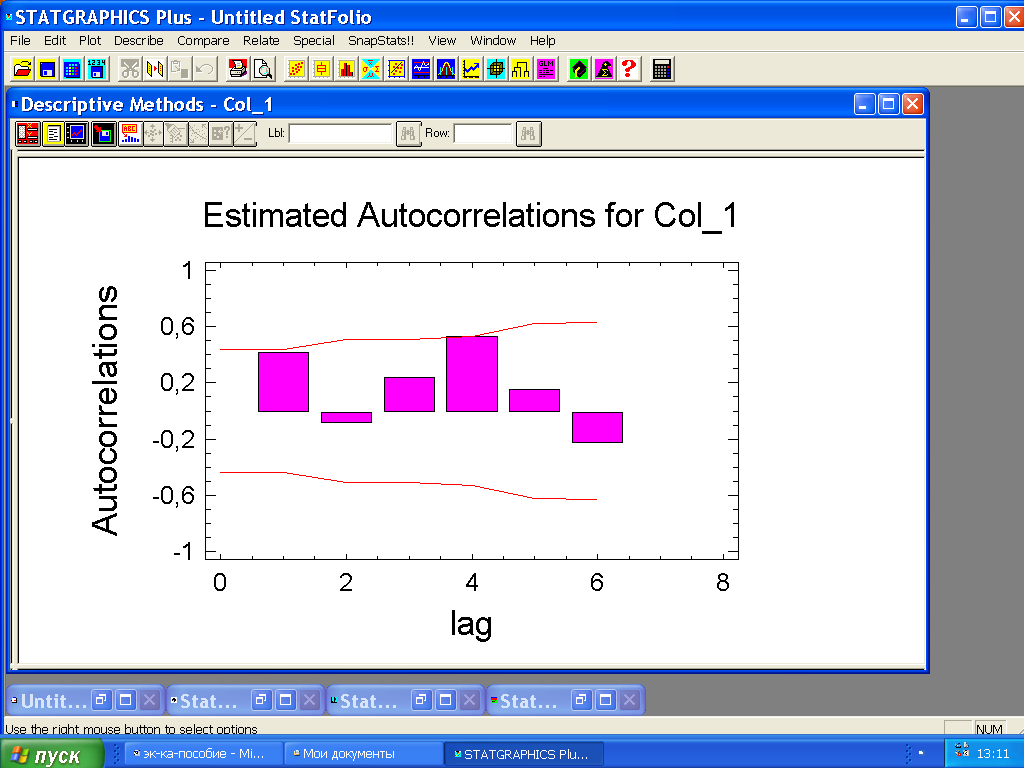
Рис. 54. Коррелограмма для временного ряда с сезонной составляющей и трендом

При комбинации разных видов зависимостей между уровнями элементов временного ряда наблюдается более сложная картина изменения коэффициентов автокорреляции. Для более сложных зависимостей необходимы и более сложные методы их анализа, например, ARIMA– модели, которые здесь не рассматриваются.