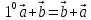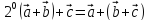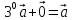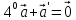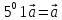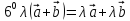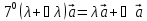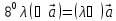Математика
.docxМатематика. Преподаватель: Александр Михайлович Сентябрь 2012
АНАЛИТИЧЕСКАЯ ГЕОМЕТРИЯ.
Метод координат.
Числовая ось – прямая (линия) на которой указывается направление, начало и масштаб.
В С А ~ 2






-
1 2
Числовая ось устанавливает взаимно-однозначное соответствие между геометрическим объектом – точками, прямыми; и числовым объектом – множество чисел.
Определение: Декартовой системой координат на плоскости называется совокупность двух взаимно-ортогональных совмещенных началами, имеющих одинаковый масштаб числовых осей.

2 у
1 х2

 х1 х
х1 х
 0
1 1
0
1 1
ДСК на плоскости устанавливает взаимно-однозначное соответствие между точками плоскости (элементами геометрического множества) и элементами числового множества (упорядоченными парами чисел).
Аналогично в пространстве.
ДКС называется совокупность трёх совмещенных началами ортогональных (прямым углом), имеющих одинаковый масштаб.
 z
z
С(0,0,1)
 1
1



 0 В(0,1,0)
0 В(0,1,0)
 1 1 y
1 1 y
А(1,0,0)
x
Рисунок 1.
Замечание: система представлена на рисунке 1 называется правой, изменение направления любой из осей превращается её в левую, двух осей снова в правую, трех осей снова в левую.
ТИПОВЫЕ ЗАДАЧИ РЕШАЕМЫЕ В АНАЛИТИЧЕСКОЙ ГЕОМЕТРИИ

В





А




хА хВ
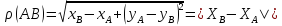
Деление отрезка в точке отношения.









y B
m
с
n

 A
A
хА хC хВ
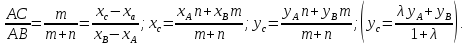
ВЕКТОРЫ. АЛГЕБРА ВЕКТОРОВ.

y
 A
A

 х
х
 0
1
0
1
Данный
объект в методе координат может быть
представлен следующим образом:

Свободный вектор – множество всех геометрических векторов имеющих одинаковую длину и направление.
Замечание: в силу определения свободного вектора всё это множество можно рассматривать как один вектор выходящий из начала координат.
ОПЕРАЦИИ НАД ВЕКТОРАМИ. ЛИНЕЙНЫЕ ОПЕРАЦИИ.
-
Сложение векторов
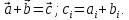
-
Сложение векторов
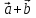
Замечание: данному правилу сложения соответствует в представлении отрезка – правило параллелограмма.

y

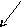



 A
A



 х
х
 0 bxax
0 bxax 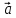 сx
сx
Умножение
вектора на число:
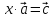
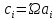
Аксиомы линейности.
Аксиома коммутативности.