
- •Методические указания практическим занятиям
- •Практическое занятие №1 Формула Коши
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №2 временные и частотные характеристики автоматических систем (ас)
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №3 структурные схемы автоматических систем (ас)
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №4 теория устойчивости движения
- •Краткие теоретические сведения
- •Теорема Ляпунова об устойчивости по первому приближению
- •Критерий Гурвица
- •Критерий устойчивости Михайлова
- •Задачи для самостоятельного решения
- •Практическое занятие №5 Уравнение Эйлера
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №6 Уравнение Эйлера-Пуассона
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №7 Вариационные задачи на условный экстремум
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №8 Принцип максимума Понтрягина
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №9 Динамическое программирование
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Билиографический список
- •Методические указания к практическим занятиям по дисциплине
Практическое занятие №3 структурные схемы автоматических систем (ас)
Цель занятия: Определение передаточной функции АС, заданной своей структурной схемой.
Краткие теоретические сведения
Структурной схемой в теории автоматического управления называют графическое изображение математической модели автоматической системы в виде соединения звеньев. Звено на структурной схеме условно обозначается в виде прямоугольника с указанием входных и выходных величин, а также передаточной функции внутри него.
Передаточную функцию АС, заданной своей структурной схемой, можно получить, например, с помощью эквивалентных преобразований. При эквивалентных преобразованиях структурных схем АС используют следующие замены:
а)
параллельное соединение звеньев
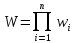 ;
;
б) антипараллельное соединение звеньев:
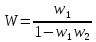
(положительная
обратная связь, звено
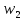 в обратной связи);
в обратной связи);
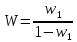
(положительная обратная связь, без звена обратной связи);
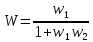
(отрицательная
обратная связь, звено
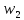 в обратной связи);
в обратной связи);
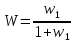
(отрицательная обратная связь, без звена обратной связи).
Пример
решения задачи.
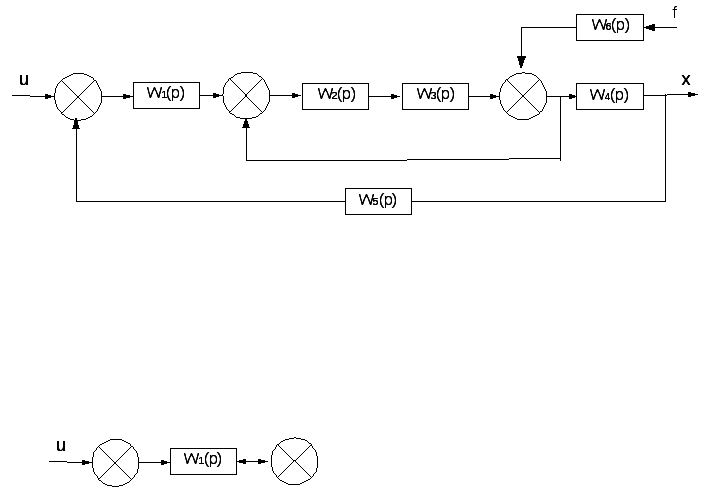
Найти
передаточную функцию АС по входному
сигналу
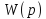 ,
если её работа описывается структурной
схемой, приведенной на рис. 3.1.
,
если её работа описывается структурной
схемой, приведенной на рис. 3.1.

Рис. 3.1
Решение. В структурной схеме рассматриваемой АС заменим каждую пару последовательно соединенных звеньев одним звеном (рис. 3.2),

Рис. 3.2
где
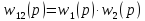 ,
, ,
,
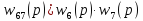 .
.
Заменим участок АС с местной положительной обратной связью (рис. 3.3) одним звеном,

Рис. 3.3
где
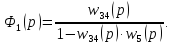
Заменим три последовательно соединённых звена (рис. 3.4) одним звеном,

Рис. 3.4
где
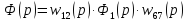 - передаточная функция разомкнутой АС.
Передаточная функция по входному сигналу
замкнутой АС имеет вид
- передаточная функция разомкнутой АС.
Передаточная функция по входному сигналу
замкнутой АС имеет вид
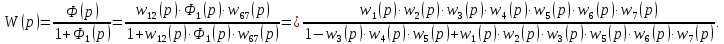
Задачи для самостоятельного решения
Найти передаточные функции АС по входному сигналу
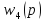 и внешнему возмущению
и внешнему возмущению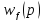 ,
если их работа задана структурными
схемами.
,
если их работа задана структурными
схемами.
а)
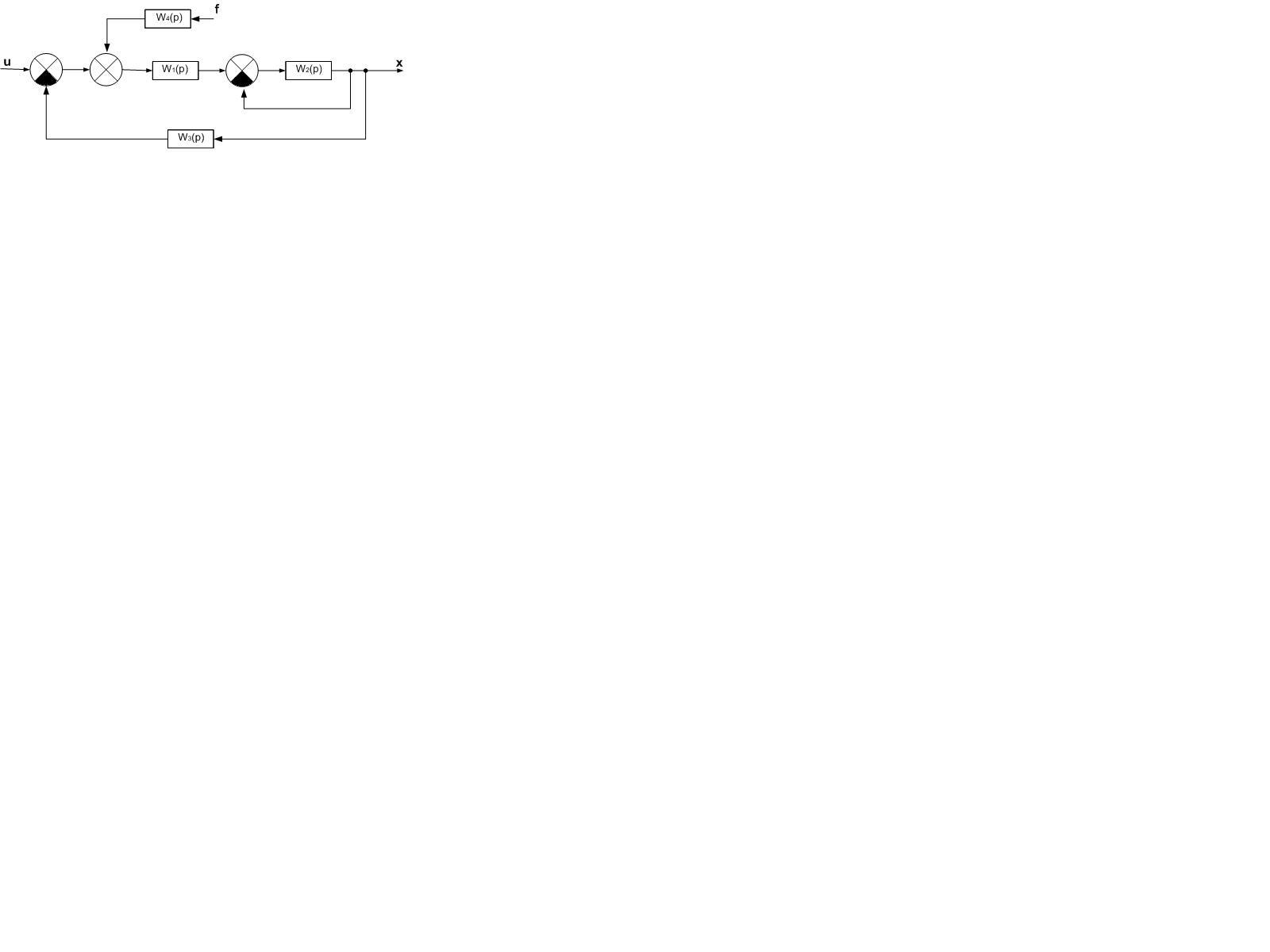
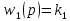 ,
,
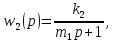
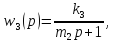
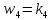 ;
;
б)
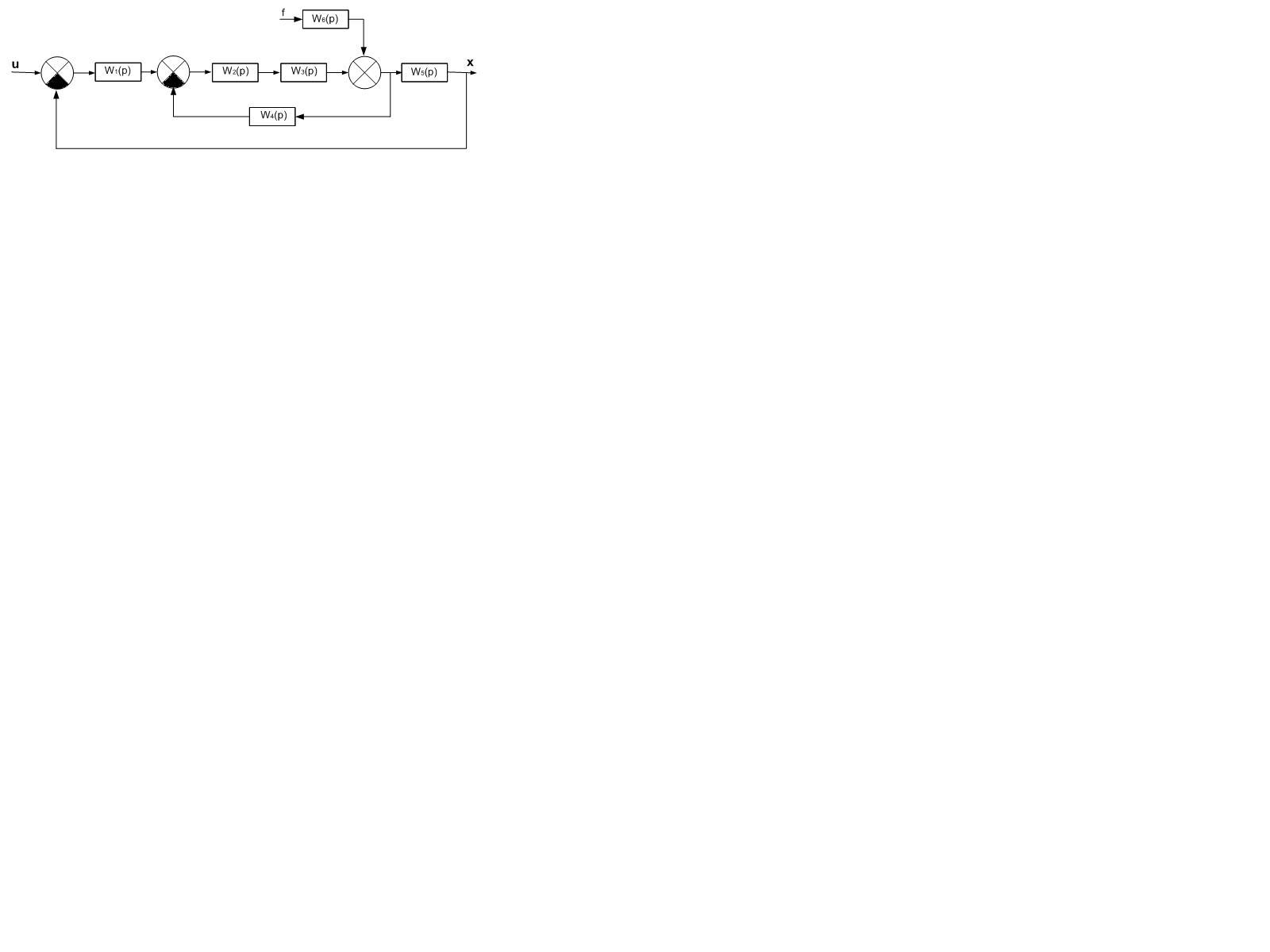
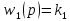 ,
,
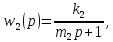
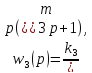
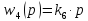 ,
,
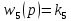 ,
,
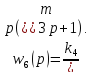
в)
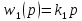 ,
,
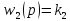 ,
,
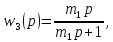
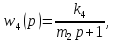
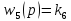 ,
,
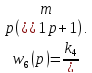
г)

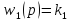 ,
,
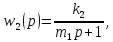
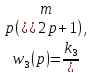
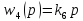 ,
,
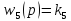 ,
,
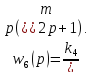
Практическое занятие №4 теория устойчивости движения
Цель занятия: Исследование устойчивости линейных систем автоматического управления по алгебраическим и частотным критериям
устойчивости.
Краткие теоретические сведения
Пусть поведение некоторой физической системы описывается системой уравнений вида:
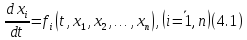
или в векторной форме:
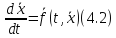
где
 ,
,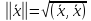 ,
,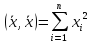 .
.
Система (4.1)-(4.2) может описывать работу САР, некоторые физические, химические, биологические процессы.
Решение
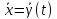 называетсяустойчивым
по Ляпунову,
если для любого
называетсяустойчивым
по Ляпунову,
если для любого
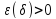 существует такое
существует такое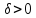 ,
что для всякого решения
,
что для всякого решения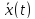 той же системы, начальное значение
которого удовлетворяет неравенству:
той же системы, начальное значение
которого удовлетворяет неравенству:
 ,
(4.3)
,
(4.3)
при
всех
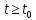 выполняется неравенство:
выполняется неравенство:
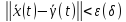 .
.
Если
же для некоторого
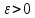 такого
такого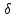 не существует, то решение
не существует, то решение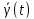 называетсянеустойчивым.
называетсянеустойчивым.
Решение
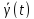 называетсяасимптотически
устойчивым, если оно устойчиво по
Ляпунову и, кроме того, все решения с
достаточно близкими начальными условиями
неограниченно приближаются к
называетсяасимптотически
устойчивым, если оно устойчиво по
Ляпунову и, кроме того, все решения с
достаточно близкими начальными условиями
неограниченно приближаются к
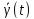 при
при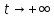 ,
то есть если из неравенства (4.3) следует
выполнение условия:
,
то есть если из неравенства (4.3) следует
выполнение условия:
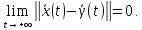
Замечание.
Наличие или отсутствие устойчивости
не зависит от выбора
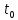 .
.
Вопрос
об устойчивости решения
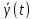 системы (4.2) можно свести к исследованию
на устойчивость нулевого (тривиального)
решения
системы (4.2) можно свести к исследованию
на устойчивость нулевого (тривиального)
решения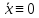 некоторой системы, аналогичной системе
(4.2):
некоторой системы, аналогичной системе
(4.2):
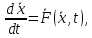
где
 .
.
При
этом решение
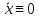 называютневозмущенным
движением.
называютневозмущенным
движением.
