
- •Методические указания практическим занятиям
- •Практическое занятие №1 Формула Коши
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №2 временные и частотные характеристики автоматических систем (ас)
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №3 структурные схемы автоматических систем (ас)
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №4 теория устойчивости движения
- •Краткие теоретические сведения
- •Теорема Ляпунова об устойчивости по первому приближению
- •Критерий Гурвица
- •Критерий устойчивости Михайлова
- •Задачи для самостоятельного решения
- •Практическое занятие №5 Уравнение Эйлера
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №6 Уравнение Эйлера-Пуассона
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №7 Вариационные задачи на условный экстремум
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №8 Принцип максимума Понтрягина
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Практическое занятие №9 Динамическое программирование
- •Краткие теоретические сведения
- •Задачи для самостоятельного решения
- •Билиографический список
- •Методические указания к практическим занятиям по дисциплине
Министерство образования и науки Российской Федерации
Южно-Российский государственный технический университет
(Новочеркасский политехнический институт)
“ОСНОВЫ ТЕОРИИ УПРАВЛЕНИЯ”
Методические указания практическим занятиям
Новочеркасск
ЮРГТУ(НПИ)
2011
УДК 338.24:681.3(076.5)
Рецензент- В.И. Маринин, заведующий кафедрой «Информатика»,
канд. техн. наук, профессор.
Скоба А.Н., Тищенко С.Н.
“Основы теории управления”. Методические указания к практическим работам /Юж.- Рос. гос. техн. ун.- т.– Новочеркасск: ЮРГТУ, 2011.– 37 с.
Указания включают краткую теорию и примеры решения задач. Для каждого практического занятия приведены примеры и задачи, которые рекомендуется решать как в аудитории, так и дома.
Предназначены для студентов специальностей 23010265 – “Автоматизированные системы обработки информации и управления”, 23020165 – “Информационные системы и технологии”, а также бакалавров по направлениям: 23040062 – “Информационные системы и технологии”, 20010062 – “ Приборостроение”.
© Южно-Российский государственный
технический университет, 2011
© Скоба А.Н., Тищенко С.Н., 2011
Практическое занятие №1 Формула Коши
Цель занятия: Представление решения управляемых систем по формуле Коши.
Краткие теоретические сведения
Нормальной системой или системой в нормальной форме Коши называют систему дифференциальных уравнений первого порядка, разрешённую относительно производных:
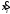 =
=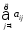
 +
+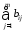
 +
+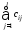
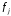 ,
,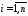 ,
(1.1)
,
(1.1)
Или
в матричной форме:
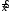 =
=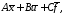
где
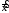 =
=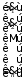 ,
,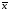 =
=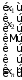 ,
,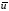 =
=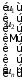 ,
, =
=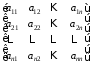 ,
,
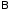 =
=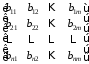 ,
,
C=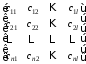 ,
,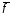 =
=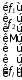 .
.
Вектор
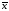 =(
=(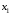 ,
,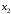 ,…,
,…,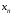 )T
– фазовый
вектор траектории развития процесса;
)T
– фазовый
вектор траектории развития процесса;
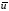 =(
=(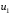 ,
,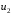 ,…,
,…,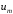 )T–
вектор управлений;
)T–
вектор управлений;
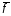 =(
=(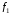 ,
,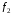 ,…,
,…,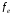 )T
– вектор
внешних возмущений, действующих на
систему;
)T
– вектор
внешних возмущений, действующих на
систему;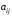 ,
,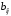 ,
,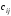 -const.
-const.
Формула
Коши для постоянных матриц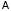 ,
,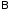 ,C имеет вид
,C имеет вид

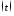 =
=
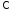
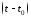
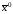 +
+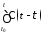
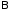
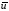 (
( )
)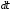 +
+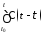 C
C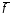 (
( )
)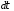 ,
(1.2)
,
(1.2)
где
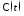 – фундаментальная матрица решений
соответствующей однородной системы
– фундаментальная матрица решений
соответствующей однородной системы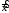 =
=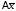 ;
;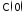 =
=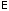 (
(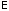 -единичная
матрица);
-единичная
матрица);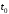 –
начальный момент времени,
–
начальный момент времени,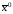 –
начальное положение системы.
–
начальное положение системы.
Пример
решения задачи.При
сильном упрощении задачи, уравнения
движения двигателя постоянного тока
имеют вид:
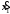 =
=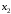 ;
; =
=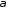
 ,
где
,
где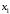 -отклонение
угла
-отклонение
угла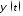 поворота якоря от некоторого фиксированного
движения
поворота якоря от некоторого фиксированного
движения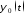 ;
;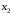 =
=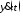 -
-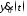 -отклонение
угловой скорости;
-отклонение
угловой скорости; =const
– величина,
пропорциональная неизменному току
якоря;
=const
– величина,
пропорциональная неизменному току
якоря;
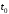 =0,
=0,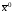 =
=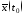 =
=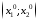 =
=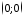 ;
;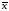
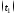 =
=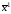 =
=
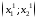 ;
;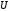 – управляющее воздействие. По формуле
Коши написать выражения для
– управляющее воздействие. По формуле
Коши написать выражения для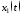 и
и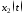 .
.
Решение. Решим однородную систему
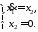 (1.3)
(1.3)
Решения
ищутся в виде:
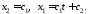 Частные
решения системы (1.3) имеют вид:
Частные
решения системы (1.3) имеют вид: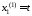 ,
,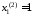 ;
;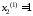 ,
,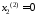 .
.
Составим
из них матрицу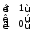 .
.
Данная
матрица не является фундаментальной,
т.к.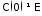 .
В построенной матрице переставим столбцы
местами, тогда получим:
.
В построенной матрице переставим столбцы
местами, тогда получим:
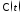

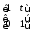 и
и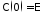 .
.
По формуле (1.2) получаем:
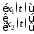 =
=
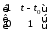
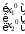 +
+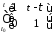

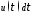 =
=
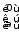
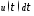
Распишем это матричное равенство по строкам:
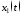

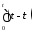
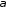
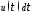

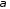

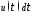 ,
,
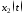

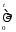
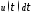

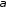
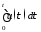 .
.
Задачи для самостоятельного решения
1.
Уравнения движения материальной точки
массой m
под действием силы тяжести P
и управляющей силы U
(P
и U
лежат в одной плоскости) приводятся к
виду
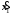

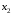 ,
,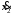

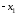

 .
.
Выразить
 и
и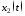 по формуле Коши, если
по формуле Коши, если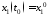 ,
,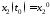 .
.
2. Написать решение по формуле Коши для управляемых систем:
а)
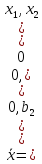
б)
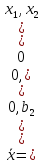
в)
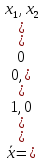
г)
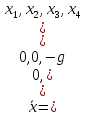
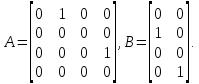
Практическое занятие №2 временные и частотные характеристики автоматических систем (ас)
Цель занятия: Получение практических навыков определения временных и частотных характеристик автоматических систем.
