9.2. Криволинейные интегралы

9.2.1. Вычисление криволинейных интегралов по длине дуги. Пусть – функция, заданная на гладкой кривойL. Если L кусочно-гладкая, то соответственно интеграл можно представить суммой интегралов погладким кускам.

.

Пусть гладкая кривая задана уравнением ,. Функцияопределена и непрерывна в точках кривойL, причём – дифференцируемая функция.

Ранее была получена формула для дифференциала дуги: . Так как в точках кривойL функция , то, причём. Подставим полученное представление функции в исходный интеграл и получим:

.

Аналогично, если кривая задана уравнением ,, то. Тогда получаем

.

Таким образом, вычисление интеграла по кривой сводится к вычислению интеграла по отрезку изменения одной из переменных.

Если гладкая кривая L задана параметрическими уравнениями:

, ,

и инепрерывные и дифференцируемые функции, причем, аопределена на, тогда. Получаем

. (6)

Если L – гладкая пространственная кривая, заданная параметрическими уравнениями:

, ,

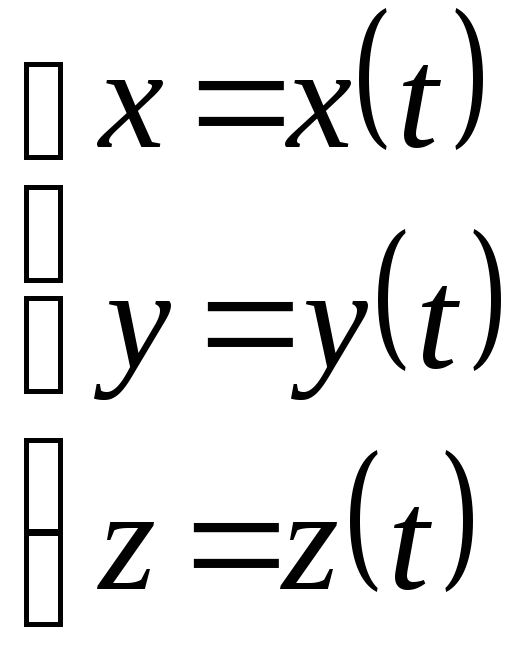тогда , а интеграл вычисляется по формуле:

. (7)

Если L – гладкая кривая, заданная на плоскости полярным уравнением , , тогда с учетом того, что 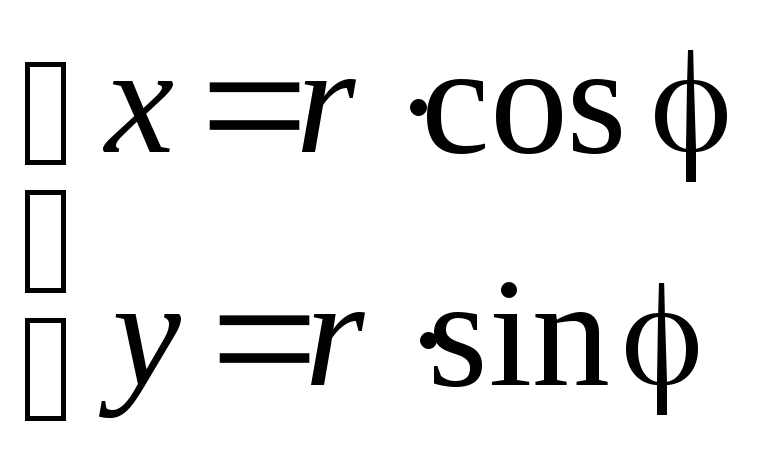, получаем. Подставим в (6) и после преобразований получим

. (8)

Пример 1. Найти длину первого витка винтовой линии, заданной уравнениеми ,.

□ По формуле (7) будем иметь

. <

Пример 2. Вычислить криволинейный интеграл первого рода , где кривая– астроида.

□Запишем параметрические уравнения астроиды ,,. Так как,, то.

Отметим, что в четырех точках. Таким образом, астроида является кусочно-гладкой кривой. Получаем

. n

Пример 3. Вычислить криволинейный интеграл первого рода , где– кривая, заданная уравнением.

□ Перейдем к полярным координатам: , . Уравнение кривой примет вид

, .

Так как

, ,

то

9.2.2. Криволинейный интеграл iIрода

П

Рис.10

устьL – гладкая ориентированная кривая в и– единичный вектор касательный в точке, а– векторная функция определённая и непрерывная наL (рис. 14). Тогда скалярное произведение есть скалярная функция, определённая в каждой точке кривой L .

Определение 3. Криволинейный интеграл первого рода по кривой от функцииназываетсякриволинейным интегралом II рода от векторной функции по кривой_:

.

Учитывая, что получаем:

. (9)

В декартовой системе координат векторы имеют координаты:

,

,

,

тогда

или

.

Криволинейный интеграл второго рода обладает, как и криволинейный интеграл первого рода, свойствами линейности и аддитивности, а также очень важным дополнительным свойством: он меняет знак при изменении ориентации кривой, т.е.

.

Докажем это утверждение. Действительно, если кривой соответствует касательный вектор, то, тогда

Если L – непрерывная кусочно-гладкая кривая, то представим её как объединение конечного числа гладких кривых ,, т.е.. Тогда по определению получаем:.

9.2.3. Вычисление криволинейного интеграла II рода. Если кривая L – гладкая и имеет векторное представление ,, то, где. Вычислив скалярное произведение в декартовой системе координат, получим формулу для вычисления криволинейного интеграла:

.

Если – плоское поле и кривая задана в явном виде, т.е.,, то криволинейный интеграл вычисляется по формуле:

,

так как ,,,.

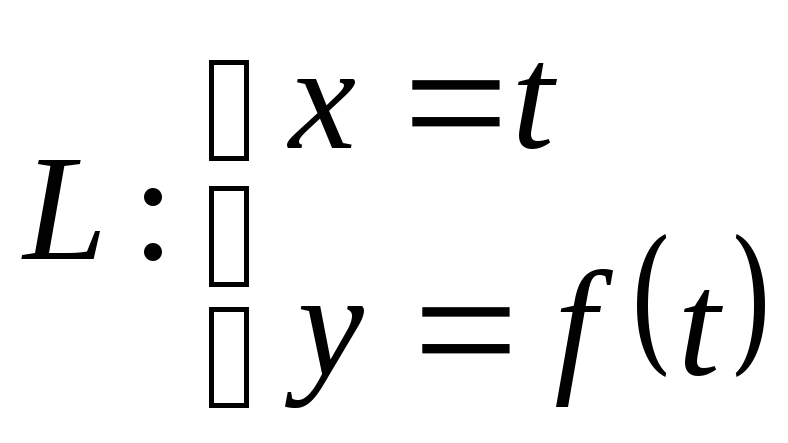Пример 4. Вычислить криволинейный интеграл второго рода по трем кривым, соединяющим точкии, изображенный на рис.11.

Решение. 1. Пусть кривая АВ задана уравнением . Тогда, получаем

.

2

. Для кривойАВ, заданной уравнением , имеем, откуда

.

3

Рис.11

. Интегрируя по ломаннойАСВ, воспользуемся свойством аддитивности интеграла и представим его как сумму двух интегралов – по отрезкам АС и СВ. Так как для отрезка АС ,и, то получаем:

.

Для отрезка СВ имеем ,и, поэтому

.

Следовательно,

.

Таким образом, . Этот результат не случаен. Далее будет доказано, что значение данного интегралане зависит от кривой, соединяющей точкиА и В.

Пример 5. Вычислить криволинейный интеграл второго рода , где– окружность.

Решение. Запишем параметрическое уравнение данной окружности: ,,. Так как,, то

.