
- •Глава 9. Криволинейные и кратные и кратные интегралы
- •9.1. Интегралы по компактной фигуре
- •9.1.1. Определение и существование интегралов по фигуре
- •9.1.2. Свойства интегралов
- •9.1.3. Геометрический и физический смысл интегралов по фигуре
- •9.2. Криволинейные интегралы
- •9.2.2. Криволинейный интеграл iIрода
- •9.3. Двойные интегралы
- •9.3.1. Вычисление двойных интегралов. Основным способом вычисления двойных интегралов является сведение их к повторным однократным интегралам. Сначала рассмотрим случай прямоугольной области.
- •9.4. Поверхностные интегралы
- •9.4.1. Вычисление поверхностного интеграла Iрода.
- •9.4.2. Поверхностный интеграл iIрода.
- •9.4. Тройные интегралы
- •9.4.1. Вычисление тройного интеграла в декартовой системе координат
- •9.5. Интегралы, зависящие от параметра
- •9.5.1. Собственные интегралы, зависящие от параметра. Рассмотрим следующий интеграл:
- •9.6.2. Несобственные интегралы, зависящие от параметра. Пусть функция определена на множестве. Будем рассматривать интегралы вида:
- •9.6. Контрольные вопросы
- •9.7. Задания для самостоятельной работы
Глава 9. Криволинейные и кратные и кратные интегралы
9.1. Интегралы по компактной фигуре
9.1.1. Определение и существование интегралов по фигуре
Компактной
фигурой в
![]() (n=1,2,3)
назовём следующие геометрические
объекты:
(n=1,2,3)
назовём следующие геометрические
объекты:
отрезок [a, b] числовой прямой;
спрямляемую кривую конечной длины L на плоскости
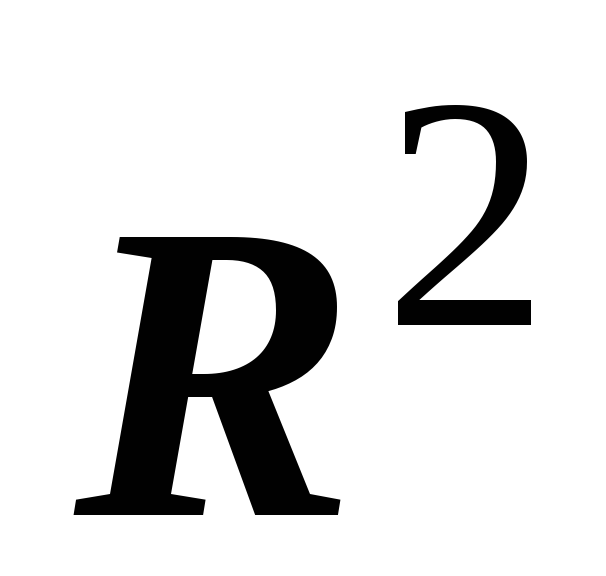 или в пространстве
или в пространстве
 ;
;
область D на плоскости
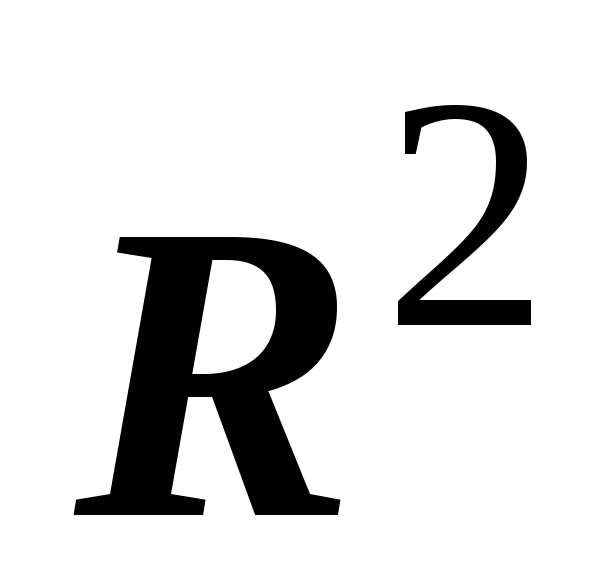 ,
ограниченную замкнутой кусочно-гладкой
кривой;
,
ограниченную замкнутой кусочно-гладкой
кривой; ограниченную поверхность
 в пространстве
в пространстве
 ;
;ограниченную область
 в пространстве
в пространстве
 .
.
Введем для компактной
фигуры общее обозначение
![]() .
.
Диаметром
компактной фигуры
называется точная верхняя грань
расстояний между любыми двумя точками
этой фигуры, т.е.
![]() ,
,
![]() .
.
Геометрически
диаметр фигуры есть наибольшая из её
хорд. Если
![]() ,
то фигура стягивается в точку. Таким
образом, компактная фигура
– это фигура с конечным диаметром d.
,
то фигура стягивается в точку. Таким
образом, компактная фигура
– это фигура с конечным диаметром d.
Для каждой компактной
фигуры
![]() определим понятие меры
определим понятие меры
![]() .
Если
.
Если
![]() ,
,
![]() .
Если
.
Если
![]() есть кривая
есть кривая
![]() на плоскости или в пространстве, то
на плоскости или в пространстве, то![]() ,
то есть длина кривой
,
то есть длина кривой![]() ,
согласно определению, сделанному ранее.
,
согласно определению, сделанному ранее.
Пусть
![]() – область на плоскости Oxy,
ограниченная замкнутой кривой. Нанесем
на область
– область на плоскости Oxy,
ограниченная замкнутой кривой. Нанесем
на область
![]() сетку с помощью двух семейств ортогональных
прямых, параллельных осям координатОх
и Оу
соответственно. Тогда область
сетку с помощью двух семейств ортогональных
прямых, параллельных осям координатОх
и Оу
соответственно. Тогда область
![]() покроется сетью целых прямоугольников
покроется сетью целых прямоугольников![]() (
(![]() )
и некоторыми нерегулярными областями
вдоль границы области. Площадь каждого
прямоугольника
)
и некоторыми нерегулярными областями
вдоль границы области. Площадь каждого
прямоугольника![]() равна
равна![]() ,
где
,
где![]() и
и![]() длина и высота прямоугольника, а
длина и высота прямоугольника, а![]() – диаметр прямоугольника. Обозначим
– диаметр прямоугольника. Обозначим![]() .
.
Площадью
области
![]() называется предел
называется предел![]() суммы площадей элементарных прямоугольников
суммы площадей элементарных прямоугольников![]() ,
когда
,
когда![]()
![]() .
.
Если этот предел
существует, то область называется
квадратируемой,
а площадь области
![]() называется мерой области и обозначается
называется мерой области и обозначается![]() .
.
Рассмотрим в
пространстве замкнутую гладкую
поверхность
![]() ,
ограниченную кусочно-гладким контуром.
Представьте себе, что эта поверхность
при помощи двух семейств ортогональных
кривых разбита на сеть элементарных
поверхностей
,
ограниченную кусочно-гладким контуром.
Представьте себе, что эта поверхность
при помощи двух семейств ортогональных
кривых разбита на сеть элементарных
поверхностей![]() (
(![]() ).
На каждой части
).
На каждой части![]() возьмем произвольную точку
возьмем произвольную точку![]() (
(![]() ).
Элемент
).
Элемент![]() проецируем на касательную плоскость,
проведенную в точке
проецируем на касательную плоскость,
проведенную в точке![]() .
В проекции получим плоскую фигуру
.
В проекции получим плоскую фигуру![]() с площадью
с площадью![]() .
обозначим
.
обозначим![]() ,
где
,
где![]() диаметр
диаметр![]() .
.
Площадью поверхности
![]() называется предел
называется предел![]() суммы площадей
суммы площадей![]() при условии
при условии![]()
![]() .
.
Если этот предел
существует, то поверхность называется
квадратируемой,
а площадь поверхности
![]() называется мерой поверхности и
обозначается
называется мерой поверхности и
обозначается![]() .
.
Теперь пусть
![]() есть область
есть область
![]() в пространствеOxyz,
ограниченная замкнутой поверхностью.
Разобьем область
в пространствеOxyz,
ограниченная замкнутой поверхностью.
Разобьем область
![]() семейством плоскостей, параллельных
осям координатOx,
Oy,
Oz.
Тогда область
семейством плоскостей, параллельных
осям координатOx,
Oy,
Oz.
Тогда область
![]() разобьется на конечное число
параллелепипедов
разобьется на конечное число
параллелепипедов![]() (
(![]() )
и некоторое число нерегулярных
пространственных областей вдоль
поверхности, ограничивающей область
)
и некоторое число нерегулярных
пространственных областей вдоль
поверхности, ограничивающей область![]() .
Объем каждого параллелепипеда
.
Объем каждого параллелепипеда![]() равен
равен![]() ,
где
,
где![]() ,
,![]() и
и![]() длина, ширина и высота параллелепипеда.
Обозначим через
длина, ширина и высота параллелепипеда.
Обозначим через![]() диаметр параллелепипеда, а
диаметр параллелепипеда, а![]() .
.
Объемом
пространственной
области
![]() называется предел
называется предел![]() суммы объемов элементарных параллелепипедов
суммы объемов элементарных параллелепипедов![]() ,
когда
,
когда![]()
![]() .
.
Если этот предел
существует, то область называется
кубируемой,
а ее объем
![]() называется мерой области и обозначается
называется мерой области и обозначается![]() .
.
Определение 1.
Разбиением
компактной
фигуры
![]() называется
множество
называется
множество
![]() компактных фигур
компактных фигур
![]() (i=1,
2, …, n),
такое, что никакие две различные фигуры
(i=1,
2, …, n),
такое, что никакие две различные фигуры
![]() не имеют общих внутренних точек.
не имеют общих внутренних точек.
Разбиение отрезка
![]() (рис.1) разбиение кривой
(рис.1) разбиение кривой![]() (рис.2), разбиение плоской области
(рис.2), разбиение плоской области![]() (рис.3), разбиение ограниченной поверхности
(рис.3), разбиение ограниченной поверхности![]() (рис.4) и разбиение ограниченного
пространственного тела
(рис.4) и разбиение ограниченного
пространственного тела![]() (рис. 5).
(рис. 5).
Рис. 1
Рис.2

Рис. 3
Рис. 4
Рис. 5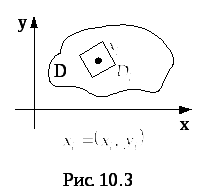

М

![]() обозначим
обозначим
![]() .
Мерами элементов разбиения
.
Мерами элементов разбиения
![]() будут соответственно
будут соответственно
![]() ,
,
![]() ;
;
![]() ;
;
![]() ;
;
![]()
![]() .
.
Пусть на фигуре
![]() задана некоторая функция
задана некоторая функция
![]() .
Для определения интеграла по фигуре
.
Для определения интеграла по фигуре
![]() сделаем следующие действия:
сделаем следующие действия:
Выполним некоторое произвольное разбиение
 фигуры
фигуры
 ,
все элементы которого имеют конечную
меру
,
все элементы которого имеют конечную
меру
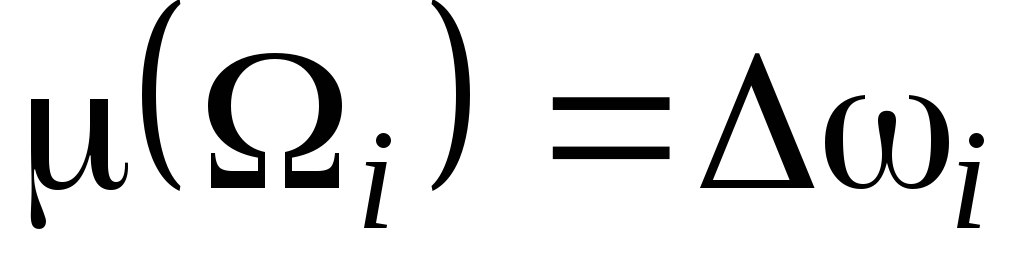 ,
причем если диаметр
,
причем если диаметр
 элемента разбиения
элемента разбиения
 стремится к нулю, то число элементов
стремится к нулю, то число элементов
 .
.На каждом элементе разбиения
 возьмем произвольную точку
возьмем произвольную точку
 .
.Вычислим значение функции f в каждой точке
 ,
получим совокупность значений
,
получим совокупность значений
 .
.Каждое значение
 умножим на меру соответствующего
элемента разбиения
умножим на меру соответствующего
элемента разбиения
 и составим сумму:
и составим сумму:
![]() (1)
(1)
Эта сумма называется
n-ой
интегральной суммой (Римана)
функции
![]() на
на
![]() ,
которая
соответствует
данному разбиению и данному выбору
точек
,
которая
соответствует
данному разбиению и данному выбору
точек
![]() .
Таких сумм можно получить бесконечно
много. Обозначим
.
Таких сумм можно получить бесконечно
много. Обозначим
![]() .
.
Определение 2.
Число I
называется пределом
интегральных сумм (1),
если
![]()
![]() ,
что при
,
что при
![]() независимо от выбора точек
независимо от выбора точек
![]() и способа разбиения выполняется
неравенство:
и способа разбиения выполняется
неравенство:
![]()
![]()
Предел I
интегральных сумм (1) при
![]() называется интегралом
от функции f(
называется интегралом
от функции f(![]() )
по фигуре
)
по фигуре
![]() .
.
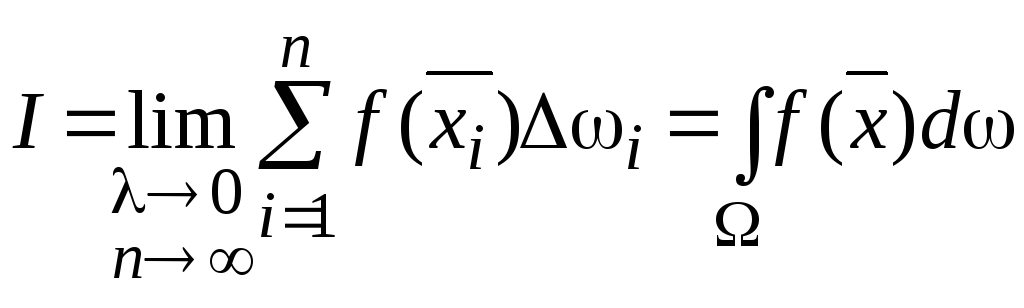 (2)
(2)
Если предел (2)
существует и не зависит от выбора точек
![]() ,
то функция
,
то функция
![]() называется интегрируемой
по Риману на компактной фигуре
называется интегрируемой
по Риману на компактной фигуре
![]() .
.
Ранее, для
определенного интеграла Римана
![]() были доказаны свойства сумм Дарбу и
свойства интегрируемых функций.
Аналогичные теоремы имеют место и здесь.
Приведём некоторые из них без
доказательства. Пусть функция
были доказаны свойства сумм Дарбу и
свойства интегрируемых функций.
Аналогичные теоремы имеют место и здесь.
Приведём некоторые из них без
доказательства. Пусть функция
![]() определена на
определена на
![]() .
.
Теорема 1
(необходимый
признак). Функция
![]() ,
интегрируемая на компактной фигуре
,
интегрируемая на компактной фигуре
![]() ,
ограничена на ней.
,
ограничена на ней.
Теорема 2
(1 достаточный признак). Функция
![]() ,
непрерывная на компактной фигуре
,
непрерывная на компактной фигуре
![]() с кусочно-гладкой границей, интегрируема
на
с кусочно-гладкой границей, интегрируема
на
![]() .
.
Теорема 3 (2
достаточный признак). Функция
![]() ,
непрерывная на компактной фигуре
,
непрерывная на компактной фигуре
![]() всюду, кроме конечных разрывов на
конечном числе гладких кривых или
поверхностей составляющих
всюду, кроме конечных разрывов на
конечном числе гладких кривых или
поверхностей составляющих
![]() ,
интегрируема на
,
интегрируема на
![]() .
.
Для каждого типа
компактной фигуры интеграл по фигуре
![]() имеет своё название и обозначение:
имеет своё название и обозначение:
1. Если
![]() ,
то
,
то
![]() – определённый
интеграл Римана.
– определённый
интеграл Римана.
2. Если
![]() ,
,
![]() или
или
![]() ,
то
,
то
![]() – криволинейный
интеграл по длине дуги или криволинейный
интеграл I
рода.
– криволинейный
интеграл по длине дуги или криволинейный
интеграл I
рода.
3. Если
![]() и
и
![]() ,
то
,
то
![]() – двойной
интеграл.
– двойной
интеграл.
4. Если
![]() и
и
![]() ,
то
,
то
![]() – поверхностный
интеграл I
рода.
– поверхностный
интеграл I
рода.
5. Если
![]() ,
,
![]() ,
то
,
то
![]() – тройной
интеграл.
– тройной
интеграл.
