
- •Глава 10. Элементы векторного анализа
- •10.1. Скалярные и векторные поля
- •10.2. Работа векторного поля. Циркуляция
- •10.3. Потенциальное векторное поле
- •10.4. Ротор векторного поля
- •10.4. Поток и дивергенция векторного поля
- •10.5. Соленоидальные векторные поля
- •10.6. Контрольные вопросы
- •10.7. Задания для самостоятельной работы
Глава 10. Элементы векторного анализа
10.1. Скалярные и векторные поля
Пусть
![]() и
и![]() – функция нескольких переменных заданная
в области
– функция нескольких переменных заданная
в области![]() ,
т.е. задано отображение
,
т.е. задано отображение![]() .
Каждой точке
.
Каждой точке![]() поставлено в соответствие действительное
число
поставлено в соответствие действительное
число![]() .
В этом случае также говорят, что в областиX
задано скалярное
поле.
.
В этом случае также говорят, что в областиX
задано скалярное
поле.
Далее будем
рассматривать пространства
![]() (плоскость) и
(плоскость) и![]() (трехмерное евклидово пространство).
Тогда соответственно скалярное поле
задаётся функцией
(трехмерное евклидово пространство).
Тогда соответственно скалярное поле
задаётся функцией![]() на плоскости и
на плоскости и
![]() в пространстве.
в пространстве.
В качестве примеров физических скалярных полей можно рассматривать: поле температуры, поле освещённости, поле плотности электрических зарядов, поле плотности масс и т.д.
Скалярные поля
![]() и
и
![]() называются также стационарными
полями.
называются также стационарными
полями.
Если
![]() или
или![]() ,
где
,
где![]() ,
тогда говорят, что скалярное поле
,
тогда говорят, что скалярное поле![]() нестационарное.
нестационарное.
Скалярное поле
имеет геометрическое изображение.
Поверхностью
уровня
скалярного
поля
![]() называют геометрическое место точек
называют геометрическое место точек![]() ,
в которых поле
,
в которых поле![]() имеет постоянное значениеС,
т.е. поверхность уровня задается
уравнением
имеет постоянное значениеС,
т.е. поверхность уровня задается
уравнением
![]() .
.
П
Рис.1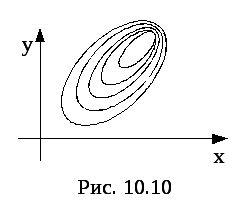
![]() и
и![]() (
(![]() )
не имеют общих точек. Взаимное расположение
поверхностей уровня даёт представление
о скалярном поле. Места сближения
поверхностей уровня соответствуют
быстрому изменению поля. Если скалярное
поле определено в области
)
не имеют общих точек. Взаимное расположение
поверхностей уровня даёт представление
о скалярном поле. Места сближения
поверхностей уровня соответствуют
быстрому изменению поля. Если скалярное
поле определено в области![]() ,
то вместо поверхностей уровня рассматриваютлинии уровня (рис.
1)
,
то вместо поверхностей уровня рассматриваютлинии уровня (рис.
1)
С помощью линий уровня изображают распределения температуры (изотермы), давления (изобары), рельеф местности на карте (горизонтали).
Ранее было определено
векторное поле, задаваемое на множестве
![]() векторной
функцией нескольких переменных (или
векторного аргумента)
векторной
функцией нескольких переменных (или
векторного аргумента)
![]() как отображение:
как отображение:![]() .
Как и в случае скалярного поля, здесь
будем рассматривать векторную функцию
.
Как и в случае скалярного поля, здесь
будем рассматривать векторную функцию![]() ,
определенную в
,
определенную в![]() и векторную функцию
и векторную функцию![]() ,
определенную в
,
определенную в![]() ..
Тогда
..
Тогда
![]() ,
,
![]() .
.
Примеры векторных
полей: электрическое поле
![]() ,
магнитное поле
,
магнитное поле![]() ,
поле скорости движения жидкости
,
поле скорости движения жидкости![]() ,
поле гравитации
,
поле гравитации![]() .
Так, если в начале координат поместить
массу
.
Так, если в начале координат поместить
массу![]() ,
то эта масса создаст поле сил тяготения
и на каждую массу
,
то эта масса создаст поле сил тяготения
и на каждую массу![]() в точке
в точке![]() действует сила равная (по закону Ньютона)
по величине
действует сила равная (по закону Ньютона)
по величине![]() и направлена к точке начала координат:
и направлена к точке начала координат:
![]() ;
;
![]() ;
;![]() ,
,
тогда
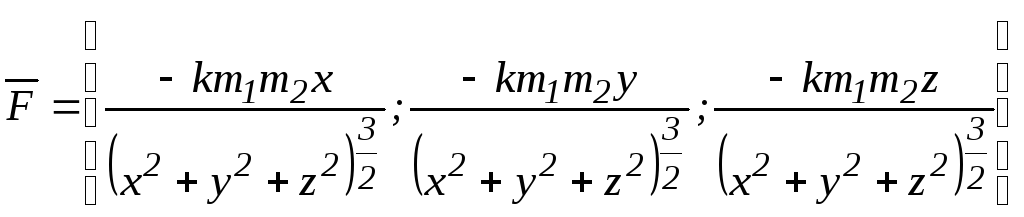 .
.
Рис.2
![]() векторное поле заданное в некоторой
области пространства. Геометрической
характеристикой векторного поля являютсявекторные (силовые) линии.
В
векторное поле заданное в некоторой
области пространства. Геометрической
характеристикой векторного поля являютсявекторные (силовые) линии.
В

![]() называется кривая, у которой касательная
называется кривая, у которой касательная![]() в каждой точке направлена вдоль заданного
в этой точке вектора поля (рис.2), т.е.
в каждой точке направлена вдоль заданного
в этой точке вектора поля (рис.2), т.е.
![]() Например, в поле скорости стационарного
потока жидкости векторными линиями
являются траектории движения частиц
жидкости.
Например, в поле скорости стационарного
потока жидкости векторными линиями
являются траектории движения частиц
жидкости.
Как и всякая кривая,
векторная линия может быть охарактеризована
своим уравнением
![]() ,
которое зависит от выбора системы
координат. Выведем уравнение векторных
линий в декартовой системе координат.
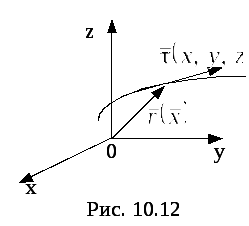
Пусть задано векторное поле
,
которое зависит от выбора системы
координат. Выведем уравнение векторных
линий в декартовой системе координат.
Пусть задано векторное поле![]() .
Вектор
.
Вектор![]() направлен по касательной к линии
направлен по касательной к линии![]() (рис.3) По определению, вектор
(рис.3) По определению, вектор![]() направлен по касательной к линии
направлен по касательной к линии![]() и коллинеарен векторному полю
и коллинеарен векторному полю![]() .
.
У
![]() (1)
(1)
Д
Рис.3![]() ,
,![]() ,
,![]() непрерывны и обладают непрерывными
частными производными. Из теоремы
существования и единственности решения
системы дифференциальных уравнений
известно, что если вектор
непрерывны и обладают непрерывными
частными производными. Из теоремы
существования и единственности решения
системы дифференциальных уравнений
известно, что если вектор![]() в точке
в точке![]() отличен от 0, то через эту точку проходит
единственная векторная линия, являющаяся
решением (1). Если
отличен от 0, то через эту точку проходит
единственная векторная линия, являющаяся
решением (1). Если![]() ,
то все знаменатели в (1) равны нулю и
через точкуМ
проходят либо бесконечное множество
кривых, либо ни одной.
,
то все знаменатели в (1) равны нулю и
через точкуМ
проходят либо бесконечное множество
кривых, либо ни одной.
П
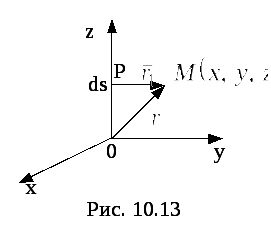
![]() по бесконечно длинному прямолинейному
проводу.
по бесконечно длинному прямолинейному
проводу.
Р
Рис.4![]() ,
определяющий напряжённость магнитного
поля. ОсьOz
направим по проводу (рис. 4). Пусть ток
течёт в положительном направлении оси
Oz.
Элемент провода по закону Био-Савара
создаёт в точке
,
определяющий напряжённость магнитного
поля. ОсьOz
направим по проводу (рис. 4). Пусть ток
течёт в положительном направлении оси
Oz.
Элемент провода по закону Био-Савара
создаёт в точке
![]() напряжённость
напряжённость![]() ,
где
,
где![]() ;
;![]() .
Отсюда
.
Отсюда![]() ,
где точка
,
где точка![]() – точка элемента провода
– точка элемента провода![]() .
Интегрируя вдоль осиOz
найдём векторное поле
.
Интегрируя вдоль осиOz
найдём векторное поле
![]() – напряжённость магнитного поля в
произвольной точкеМ:
– напряжённость магнитного поля в
произвольной точкеМ:
![]() .
.
Если
![]() ,
тогда
,
тогда![]() .
.
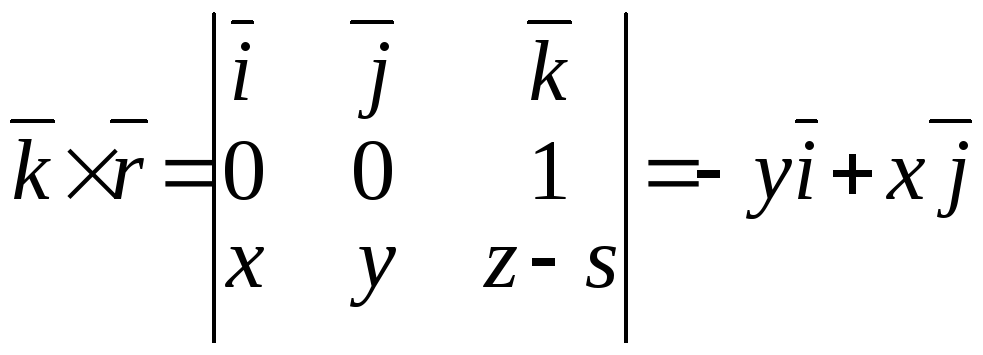 .
.
Тогда
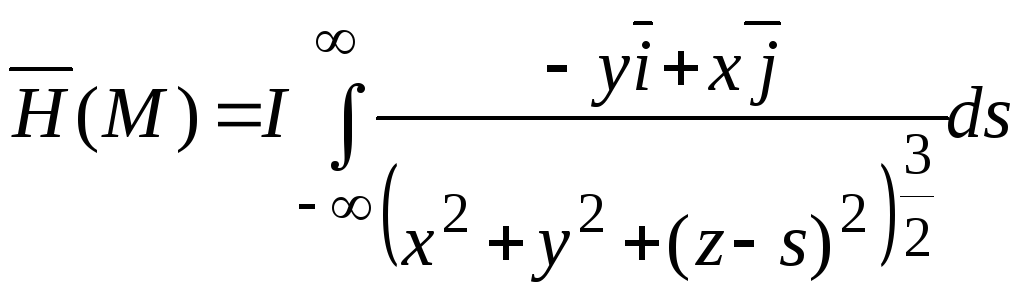 .
Заменаs-z=
.
Заменаs-z=![]() преобразует полученный интеграл
следующим образом
преобразует полученный интеграл
следующим образом
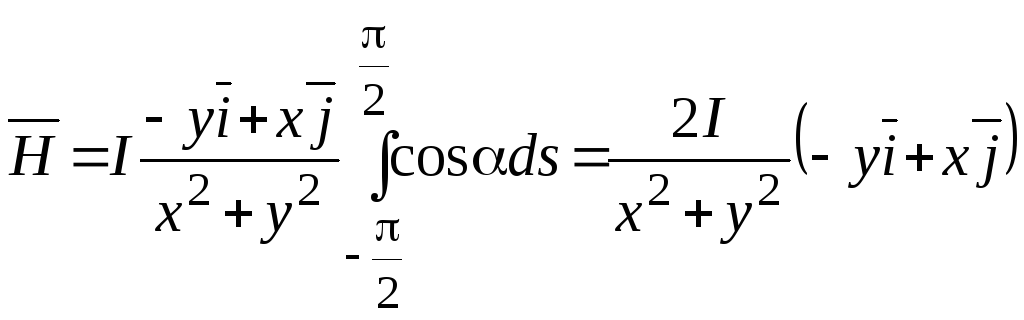 .
.
Система дифференциальных уравнений имеет вид:
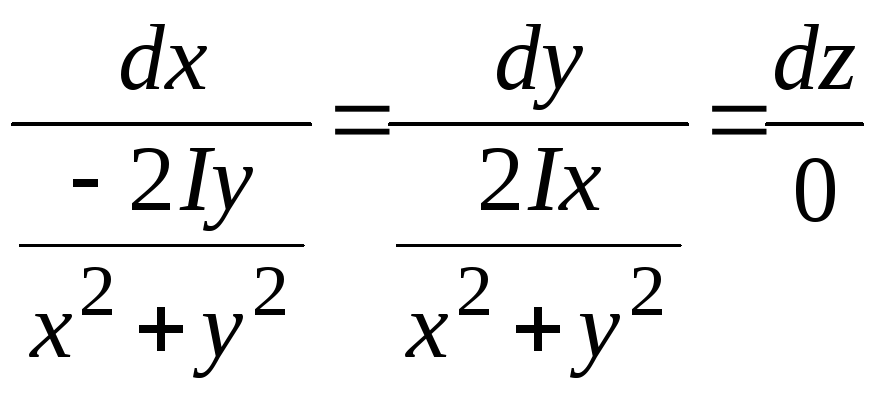 .
.
![]() .
.
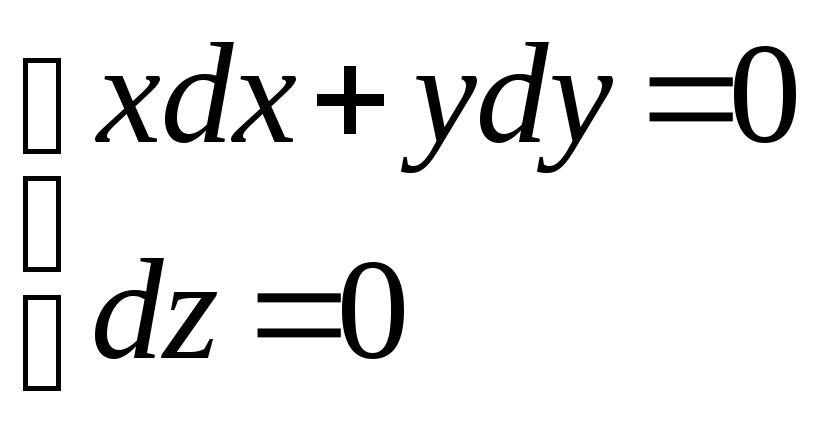 .
.
Из последнего
выражения получаем
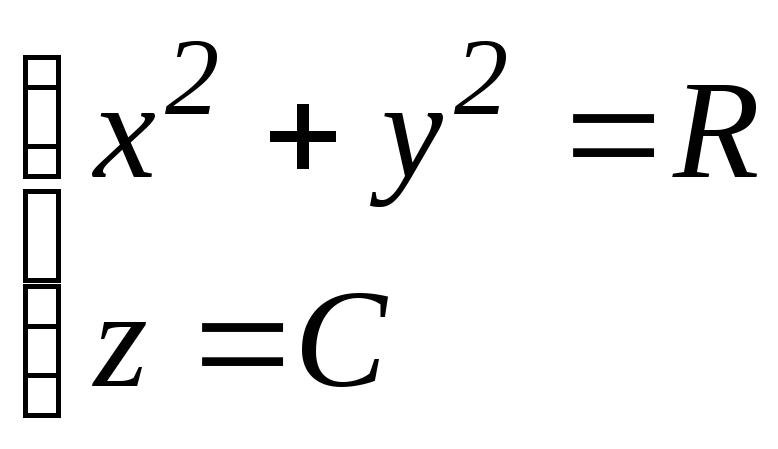 .
.
Постоянные R
и C
определяются из условия прохождения
векторной линии через определённую
точку
![]() .
Через любую точку, не лежащую на оси Oz,
проходит единственная векторная линия,
представляющая собой окружность, лежащую
в плоскости, параллельной плоскости
Oxy.
.
Через любую точку, не лежащую на оси Oz,
проходит единственная векторная линия,
представляющая собой окружность, лежащую
в плоскости, параллельной плоскости
Oxy.
