Плотность вероятности

Важнейшей характеристикой именно непрерывной случайной величины является (помимо функции распределения) плотность вероятности. Напомним, что случайная величина называется непрерывной, если ее функция распределения F(x) непрерывна на всей числовой прямой, а ее производная существует для всех х, кроме, быть может, отдельных изолированных точек. Таким образом, если Х – непрерывная случайная величина, то для всех х (кроме, быть может, отдельных изолированных точек) существует функция

.

Определенная таким образом функция f(x) называется плотностью вероятности (плотностью распределения, плотностью распределения вероятностей, дифференциальной функцией распределения) непрерывной случайной величины Х.

Рассмотрим свойства плотности вероятности н.с.в. Х , которые следуют из приведенного ее определения и описанных выше свойств функции F(x).

1. Плотность вероятности всюду неотрицательна: f(x) ≥ 0 (как производная возрастающей функции F(x)).

2. Зная функцию распределения F(x) легко по определению найти плотность вероятности: . А наоборот? Если известнаf(x), то значит известна производная . ПоэтомуF(x) является одной их первообразных для f(x) и получается из нее интегрированием. Нужная первообразная вычисляется по формуле:

.

3. Знание плотности вероятности тоже позволяет вычислить вероятность того, что при испытании случайная величина примет значение из заданного интервала (a,b):

.

Доказательство следует из того, что F(x) является первообразной для f(x) и формулы Ньютона-Лейбница и свойств функции F(x):

.

Вспоминая геометрический смысл определенного интеграла как площадь соответствующей криволинейной трапеции, можно сделать важный вывод, что на геометрическом языке вероятность принятия непрерывной случайной величиной значения внутри произвольного интервала (a,b) равна площади S фигуры, ограниченной сверху графиком плотности вероятности f(x) и опирающейся на отрезок [a,b] (рисунок).

4. Из предыдущего свойства следует, что

,

поскольку этот интеграл представляет собой вероятность достоверного события: при испытании случайная величина примет значение из интервала . Геометрически это означает, что площадь фигуры, заключенной между графиком плотности вероятности и осьюх равна 1.

5. Если плотность вероятности некоторой с.в. Х обращается в 0 вне некоторого отрезка [a,b], то: а) вероятность для с.в. Х принять значение в любом интервале, полностью лежащем вне этого отрезка, равна 0; б) выполняется соотношение

.

Доказательство а) следует из третьего свойства плотности вероятности, а б) из предыдущего свойства и свойства интегралов:

.

В связи с последним свойством примем такое определение. Непрерывная с.в. Х называется сосредоточенной на некотором отрезке [a,b], если плотность ее вероятности f(x) обращается в 0 вне этого отрезка.

Пример. Дана функция распределения с.в. Х: . Найти плотность вероятностиf(x).

Решение: по определению .

Пример. Дана плотность вероятности с.в. Х: . Найти а) значение параметраа; б) .

Решение. Для вычисления значения неизвестного параметра а воспользуемся последним свойством плотности вероятности, учитывая что она обращается в 0 вне отрезка :. Итак,, а потому. Поэтому формула для плотности вероятности выглядит следующим образом:

.

Тогда из третьего свойства плотности вероятности :

.

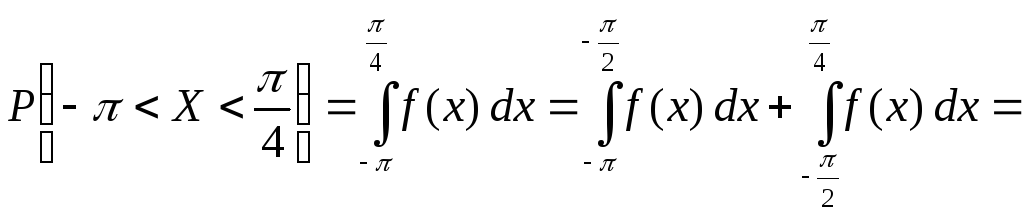
Пример. Найти функцию распределения F(x) с.в. Х из предыдущего примера (воспользоваться вторым свойством плотности вероятности).