Равномерное распределение

Перейдем теперь к часто используемым на практике распределениям непрерывной случайной величины.

Непрерывная с.в. Х называется равномерно распределенной на отрезке [a,b], если плотность ее вероятности постоянна на этом отрезке, а вне его равна 0 (т.е. случайная величина Х сосредоточена на отрезке [a,b], на котором имеет постоянную плотность). По данному определению плотность равномерно распределенной на отрезке [a,b] случайной величины Х имеет вид:

,

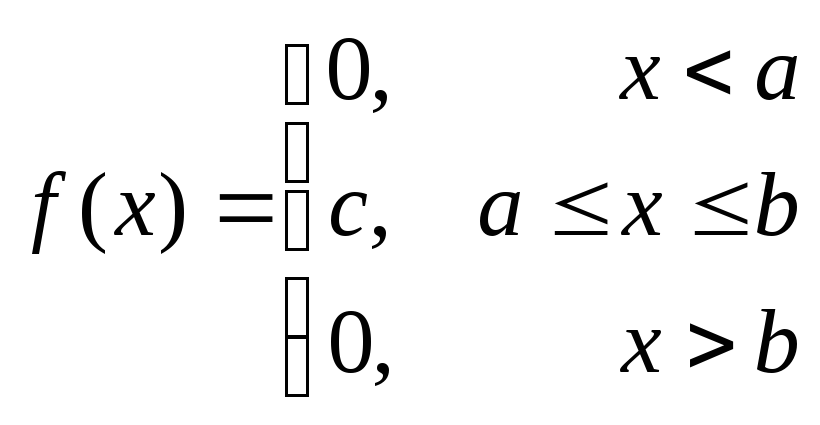где с есть некоторое число. Впрочем, его легко найти, используя свойство плотности вероятности для с.в., сосредоточенных на отрезке [a,b]: . Отсюда следует, что, откуда. Поэтомуплотность равномерно распределенной на отрезке [a,b] случайной величины Х имеет вид:

.

Судить о равномерности распределения н.с.в. Х можно из следующего соображения. Непрерывная случайная величина имеет равномерное распределение на отрезке [a,b], если она принимает значения только из этого отрезка, и любое число из этого отрезка не имеет преимущества перед другими числами этого отрезка в смысле возможности быть значением этой случайной величины.

К случайным величинам, имеющим равномерное распределение относятся такие величины, как время ожидания транспорта на остановке (при постоянном интервале движения длительность ожидания равномерно распределена на этом интервале), ошибка округления числа до целого (равномерно распределена на [−0.5, 0.5]) и другие.

Вид функции распределения F(x) равномерно распределенной отрезке [a,b] случайной величины Х ищется по известной плотности вероятности f(x) c помощью формулы их связи . В результате соответствующих вычислений получаем следующую формулу для функции распределенияF(x) равномерно распределенной отрезке [a,b] случайной величины Х :

.

На рисунках приведены графики плотности вероятности f(x) и функции распределения f(x) равномерно распределенной отрезке [a,b] случайной величины Х :

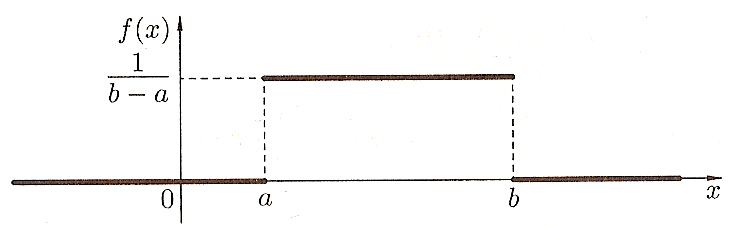
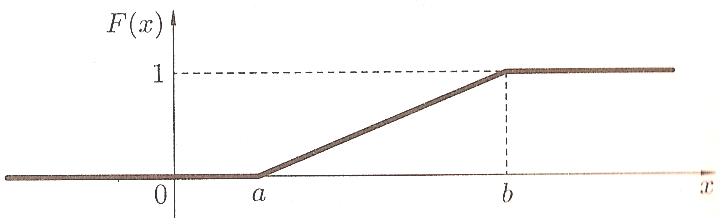
Математическое ожидание, дисперсия, среднее квадратическое отклонение, мода и медиана равномерно распределенной отрезке [a,b] случайной величины Х вычисляются по плотности вероятности f(x) обычным образом (и достаточно просто из-за простого вида f(x)). В результате получаются следующие формулы:

,

а модой d(X) является любое число отрезка [a,b].

Найдем вероятность попадания равномерно распределенной отрезке [a,b] случайной величины Х в интервал , полностью лежащий внутри [a,b]. Учитывая известный вид функции распределения, получаем:

.

Таким образом, вероятность попадания равномерно распределенной отрезке [a,b] случайной величины Х в интервал , полностью лежащий внутри [a,b], не зависит от положения этого интервала, а зависит только от его длины и прямо пропорциональна этой длине.

Пример. Интервал движения автобуса составляет 10 минут. Какова вероятность того, что пассажир, подошедший к остановке, прождет автобус менее 3 минут? Каково среднее время ожидания автобуса?

Нормальное распределение

Это распределение наиболее часто встречается на практике и играет исключительную роль в теории вероятностей и математической статистике и их приложениях, поскольку такое распределение имеют очень многие случайные величины в естествознании, экономике, психологии, социологии, военных науках и так далее. Данное распределение является предельным законом, к которому приближаются (при определенных естественных условиях) многие другие законы распределения. С помощью нормального закона распределения описываются также явления, подверженные действию многих независимых случайных факторов любой природы и любого закона их распределения. Перейдем к определениям.

Непрерывная случайная величина называется распределенной по нормальному закону (или закону Гаусса), если ее плотность вероятности имеет вид:

,

где числа а и σ (σ>0) являются параметрами этого распределения.

Как уже было сказано, закон Гаусса распределения случайных величин имеет многочисленные приложения. По этому закону распределены ошибки измерений приборами, отклонение от центра мишени при стрельбе, размеры изготовленных деталей, вес и рост людей, годовое количество осадков, количество новорожденных и многое другое.

Приведенная формула плотности вероятности нормально распределенной случайной величины содержит, как было сказано, два параметра а и σ , а потому задает семейство функций, меняющихся в зависимости от значений этих параметров. Если применить обычные методы математического анализа исследования функций и построения графиков к плотности вероятности нормального распределения, то можно сделать следующие выводы.

1. Плотность вероятности f(x)>0 для всех значений х, а потому график функции расположен над осью х.

2. Ось х является асимптотой графика при х → ± ∞, поскольку 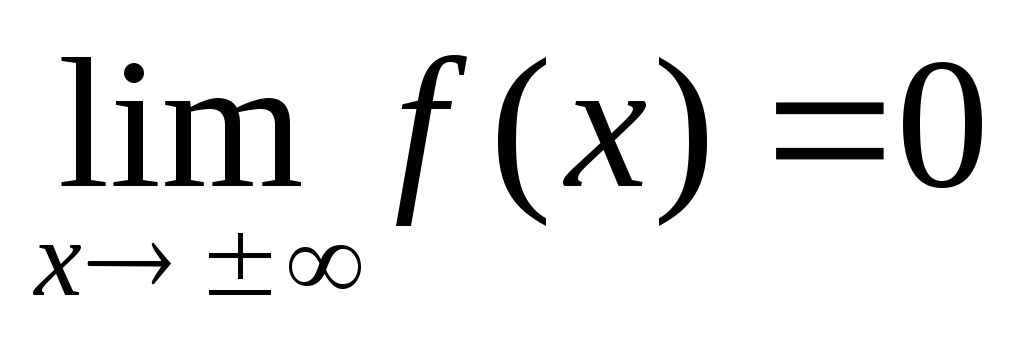. Поэтому на бесконечности график «прижимается» к осих.

3. Функция f(х) имеет единственную точку максимума х=а, а максимальное значение .

4. График функции симметричен относительно вертикальной прямой с уравнением х=а.

5. С помощью второй производной можно убедиться, что точки графика

являются точками его перегиба.

Исходя из полученной информации, строим график плотности вероятности f(x) нормального распределения (он называется кривой Гаусса − рисунок).

Выясним, как влияет изменение параметров а и σ на форму кривой Гаусса. Очевидно (это видно из формулы для плотности нормального распределения), что изменение параметра а не меняет форму кривой, а приводит лишь к ее сдвигу вправо или влево вдоль оси х. Зависимость от σ сложнее. Из проведенного выше исследования видно, как зависит величина максимуму и координаты точек перегиба от параметра σ . К тому же надо учесть, что при любых параметрах а и σ площадь под кривой Гаусса остается равной 1 (это общее свойство плотности вероятности). Из сказанного следует, что с ростом параметра σ кривая становится более пологой и вытягивается вдоль оси х. На рисунке изображены кривые Гаусса при различных значениях параметра σ ( σ₁< σ< σ₂ ) и одном и том же значении параметра а.

Выясним вероятностный смысл параметров а и σ нормального распределения. Уже из симметричности кривой Гаусса относительно вертикальной прямой, проходящей через число а на оси х понятно, что среднее значение (т.е. математическое ожидание М(Х)) нормально распределенной случайной величины равно а. Из этих же соображений мода и медиана тоже должны быть равны числу а. Точные расчеты по соответствующим формулам это подтверждают. Если же мы выписанное выше выражение для f(x) подставим в формулу для дисперсии , то после (достаточно непростого) вычисления интеграла получим в ответе числоσ². Таким образом, для случайной величины Х, распределенной по нормальному закону, получились следующие основные ее числовые характеристики:

.

Поэтому вероятностный смысл параметров нормального распределения а и σ следующий. Если с.в. Х распределена нормально с параметрами а и σ, то ее среднее значение равно а, а среднее квадратическое отклонение равно σ.

Найдем теперь функцию распределения F(x) для случайной величины Х, распределенной по нормальному закону, используя выписанное выше выражение для плотности вероятности f(x) и формулу . При подстановкеf(x) получается «неберущийся» интеграл. Все, что удается сделать для упрощения выражения для F(x), это представление этой функции в виде:

,

где Ф(х) − так называемая функция Лапласа, которая имеет вид

.

Интеграл, через который выражается функция Лапласа, тоже является неберущимися (но при каждом х этот интеграл может быть вычислен приближенно с любой наперед заданной точностью). Однако вычислять его и не потребуется, так как в конце любого учебника по теории вероятностей есть таблица для определения значений функции Ф(х) при заданном значении х. В дальнейшем нам понадобится свойство нечетности функции Лапласа: Ф(−х)= −Ф(х) для всех чисел х.

Найдем теперь вероятность того, что нормально распределенная с.в. Х примет значение из заданного числового интервала (α, β). Из общих свойств функции распределения Р(α<X< β)=F(β) − F(α). Подставляя α и β в выписанное выше выражение для F(x), получим

.

Как сказано выше, если с.в. Х распределена нормально с параметрами а и σ, то ее среднее значение равно а, а среднее квадратическое отклонение равно σ. Поэтому среднее отклонение значений этой с.в. при испытании от числа а равно σ. Но это среднее отклонение. Поэтому возможны и бо´льшие отклонения. Узнаем, насколько возможны те или иные отклонения от среднего значения. Найдем вероятность того, что значение распределенной по нормальному закону случайной величины Х отклониться от ее среднего значения М(Х)=а менее, чем на некоторое число δ, т.е. Р(|X−a|<δ ) : . Таким образом,

.

Подставляя в это равенство δ=3σ, получим вероятность того, что значение с.в. Х (при одном испытании) отклонится от среднего значения менее чем на утроенное значение σ (при среднем отклонении, как мы помним, равном σ): (значениеФ(3) взято из таблицы значений функции Лапласа). Это почти 1 ! Тогда вероятность противоположного события (что значение отклонится не менее, чем на 3σ) равна 1−0.997=0.003, что очень близко к 0. Поэтому это событие «почти невозможно» − случается крайне редко (в среднем 3 раза из 1000). Это рассуждение является обоснованием широко известного «правила трех сигм».

Правило трех сигм. Нормально распределенная случайная величина при единичном испытании практически не отклоняется от своего среднего далее, чем на 3σ.

Еще раз подчеркнем, что речь идет об одном испытании . Если испытаний случайной величины много, то вполне возможно, что какое-либо ее значение и удалится от среднего далее, чем 3σ. Это подтверждает следующий

Пример. Какова вероятность, что при 100 испытаниях нормально распределенной случайной величины Х хотя бы одно ее значение отклонится от среднего более, чем на утроенное среднее квадратическое отклонение? А при 1000 испытаниях?

Решение. Пусть событие А означает, что при испытании случайной величины Х ее значение отклонилось от среднего более, чем на 3σ. Как только что было выяснено, вероятность этого события р=Р(А)=0.003 . Проведено 100 таких испытаний. Надо узнать вероятность того, что событие А произошло хотя бы раз, т.е. произошло от 1 до 100 раз. Это типичная задача схемы Бернулли с параметрами n=100 (число независимых испытаний), р=0.003 (вероятность события А в одном испытании), q=1−p=0.997. Требуется найти Р₁₀₀(1≤k≤100). В данном случае, конечно, проще найти сначала вероятность противоположного события Р₁₀₀(0) − вероятность того, что событие А не произошло ни разу ( т.е. произошло 0 раз) . Учитывая связь вероятностей самого события и ему противоположного, получим:

.

Не так уж мало. Вполне может произойти (происходит в среднем в каждой четвертой такой серии испытаний). При 1000 испытаний по такой же схеме можно получить, что вероятность хотя бы одного отклонения далее, чем на 3σ, равно: . Так что можно с большой уверенностью дождаться хотя бы одного такого отклонения.

Пример. Рост мужчин определенной возрастной группы распределен нормально с математическим ожиданием a, и среднеквадратическим отклонением σ. Какую долю костюмов k-го роста следует предусмотреть в общем объеме производства для данной возрастной группы, если k-ый рост определяется следующими пределами:

1 рост: 158 − 164см 2 рост: 164 − 170см 3 рост: 170 − 176см 4 рост: 176 − 182см

Решение. Решим задачу при следующих значениях параметров: а=178, σ=6, k=3. Пусть с.в. Х − рост случайно выбранного мужчины (она распределена по условию нормально с заданными параметрами). Найдем вероятность того, что наугад выбранному мужчине понадобится 3-й рост. Пользуясь нечетностью функции Лапласа Ф(х) и таблицей ее значений: P(170<X<176) =Ф((176−178)/6) − Ф((170−178)/6) = Ф(−0.3333) −Ф(−1.3333)= Ф(1.3333) −Ф(0.3333)=0.4082−0.1293=0.2789. Поэтому в общем объеме производства надо предусмотреть 0.2789*100%=27.89% костюмов 3-го роста.