2) Сообщения и сигналы. Кодирование и квантование сигналов.

Сообщение – последовательность сигналов

Сообщение — наименьший элемент языка, имеющий идею или смысл, пригодный для общения. В информатике — форма представления информации, имеющая признаки начала и конца, предназначенная для передачи через среду связи. Также форма предоставления информации, совокупность знаков или первичных сигналов, содержащих информацию.

Чтобы сообщение стало сигналом его необходимо интерпретировать

Правило интерпретации сообщения - соответствие между сообщением и содержащейся в нем информацией. Однозначное правило и неоднозначное.

Неоднозначное:

1) одно и то же сообщение несет различную информацию

2) разные сообщения несут одну и ту же информацию

Сигнал – изменяемая во времени физическая величина

Сигнал (в теории информации и связи) — материальный носитель информации, используемый для передачи сообщений в системе связи. Сигнал может генерироваться, но его приём не обязателен, в отличие от сообщения, которое должно быть принято принимающей стороной, иначе оно не является сообщением. Сигналом может быть любой физический процесс, параметры которого изменяются в соответствии с передаваемым сообщением.

Сигналы бывают:

1) АНАЛОГОВЫМназывается сигнал, который может приниматьлюбоезначение на некотором промежутке.

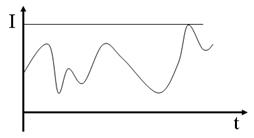
2) ДИСКРЕТНЫМ называется сигнал, который может принимать строго определенные значения на некотором промежутке

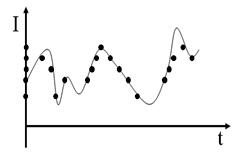
Кодирование сигнала – это его представление в определенной форме, удобной или пригодной для последующего использования сигнала. Говоря строже, это правило, описывающее отображение одного набора знаков в другой набор знаков. Тогда отображаемый набор знаков называется исходным алфавитом, а набор знаков, который используется для отображения, - кодовым алфавитом, или алфавитом для кодирования

Кодирование – преобразование информации в форму, пригодную для передачи по каналу связи.

Декодирование – преобразование информации в форму, пригодную для получения.

Двоичное кодирование

Дискретизация— преобразование непрерывной функции в дискретную.

Преобразование непрерывного информационного множества аналоговых сигналов в дискретное множество называется дискретизациейиликвантованием по уровню(ср. «Квантование по времени»).

Квантование по уровню широко используется в цифровых автоматах.

Точки на втором рисунке называется квантованием

Квантование (англ. quantization) — в информатике разбиение диапазона значений непрерывной или дискретной величины на конечное число интервалов. Существует также векторное квантование — разбиение пространства возможных значений векторной величины на конечное число областей. Простейшим видом квантования является деление целочисленного значения на натуральное число.

3) Позиционные системы счисления. Методы перевода чисел.

Система счисления – это правило записи чисел с помощью заданного набора специальных знаков – цифр.

Виды систем счисления:

• Унарная

• Непозиционные

• Позиционные

Унарной называют систему счисления, в которой для записи чисел используют только один знак – 1 (например, Счетные палочки).

Непозиционной называют систему счисления, в которой значение цифры в изображении числа не зависит от ее положения в ряду других цифр.

Достоинства:

• Красивые обозначения

Недостатки:

• Нет 0 и знаков больших М

• Громоздкая запись

• Неудобно проводить вычисления.

Позиционной называют систему счисления, в которой значение каждой цифры в изображении числа определяется ее положением (позицией) в ряду других цифр.

353,358 = 3*10²+5*10¹+3*10⁰+3*10^-1+5*10^-2+8*10^-3

Примеры:

• Десятичная

• Пятеричная

• Шестеричная

• Двенадцатеричная

• Двадцатеричная

• Шестидесятеричная и др.

Построение чисел в позиционных системах счисления

• Пусть р – основание системы счисления.

• Тогда любое число Х можно представить в виде многочлена:

X_р=a_k*p^k+a_k-1*p^k-1+…+a₁*p+a₀

• Из коэффициентов строится сокращенная запись числа:

X_р=(a_ka_k-1…a₁)_р

• Коэффициенты – целые числа 0≤a_i≤р-1

Каково минимальное значение р?

р = 1 – унарная система счисления.

р = 2 – двоичная система счисления.

р = 8

р = 16

Представление чисел в различных системах счисления

Перевод чисел из q-ричной системы счисления в р-ричную

Целые числа при q>p

Для замены исходного числа Xqравным ему числомXpнужно по правиламq-ричной арифметики целочисленно делитьXqна новое основание р. Результаты деления, записанные в обратном порядке от последнего к первому, и окажутся цифрамиXp.

Правильная дробь при q<p

Для замены исходного числа Xqравным ему числомXpнужно представить числоXqв форме многочлена и выполнить все операции по правилам р-ричной арифметики.

Выводы и рекомендации:

При переводе чисел, содержащих целую и дробную часть, они переводятся по отдельности, а затем объединяются.

1101,11₂= ?₁₀

При переводе чисел между системами, не являющимися десятичными, удобнее осуществлять перевод через десятичную в качестве промежуточной.

Х_q→X₁₀ →X_p

Рациональное число в исходной системе счисления после перехода может превратиться в иррациональное.

Иррациональное число в исходной системе счисления в иной системе может оказаться рациональным.

5,3(3)₁₀= 12,1₃

Экономичность системы счисления – то количество чисел, которое можно записать в данной системе с помощью определенного количества цифр.

12 знаков: Разбивка на группы.

Основание системы счисления	1	2	3	4	6	12
Количество чисел	12	64	81	64	36	12

Самой экономичной является троичная система счисления

Перевод чисел между системами счисления 2-8-16

Для перевода целого двоичного числа в систему счисления с основанием p=2^rдостаточно данное двоичное число разбить справа налево на группы вrцифр каждая и каждую группу независимо перевести в системуp.

110001₂=61₈

Для перевода целого числа, записанного в системе счисления с основанием p=2^r, в двоичную систему достаточно каждую цифру исходного числа независимо заменить соответствующимr-разрядным двоичным числом, дополняя его при необходимости незначащими нулями до группы вrцифр.

D3₁₆=11010011₂