1) Исходные потоки вызовов являются пуассоновскими;

2) пуассоновский характер потоков сохраняется как для избыточной, так и для пропущенной нагрузок;

3) система находится в состоянии статистического равнове­сия;

4) система с явными потерями;

5) не учитываются потери в коммутационных и управляю­щих устройствах;

6) время установления соединения равно 0.

Исходными данными при определении параметров качества об­служивания являются:

1) структура сети (расположение узлов и емкость ветвей);

2) нагрузка для обслуживания в ЧНН между узлами каж­дой пары узлов;

3) план распределения потоков на сети.

В процессе расчетов сети определяются следующие параметры качества обслуживания:

1) величины суммарной нагрузки на каждую ветвь;

2) вероятности потерь на ветвях;

3) вероятности потерь между узлами каждой пары узлов;

4) вероятность потерь в среднем на сети;

5) величины нагрузок, обслуженных и потерянных в каждом транзитном узле и на всей сети в целом.

Из перечисленных параметров наиболее важными являются ве­роятности потерь на ветвях, так как остальные параметры мо­гут быть легко вычислены через эти величины.

Расчет вероятностей потерь на ветвях в сетях с обходными направлениями осложняется тем, что вероятность потерь на каж­дой ветви в общем случае зависит от вероятностей потерь на всех остальных ветвях. Эту зависимость для вероятностей потерь на ветвях сети с учетом заданного плана распределения потоков ин­формации можно представить в виде системы алгебраических уравнений вида

где N — число узлов в сети;

М — число ветвей в сети;

Р_i — ве­роятность потерь на i-й ветви;

a(k, n) — нагрузка, исходящая из узла k и предназначенная для узла n;

0≤ f ⁱ _k,n (Р_1,Р₂,….. Рм) ≤ 1—доля нагрузки, исходящей из узла k и предназначен­ной для узла и, поступающая на i-ю ветвь в соответствии с планом распределения. Эта функция равна 0, если i-я ветвь не использу­ется ни в одном из путей, соединяющих узлы k, n, т. е. не входит в дерево путей для данной пары узлов, и равна 1, если i-я ветвь является ветвью первого выбора.

Можно указать три метода решения задачи определения потерь на ветвях. Первый метод состоит в составле­нии системы (4.21) и ее решении. Однако составление этой си­стемы уравнений является довольно трудоемким процессом уже для небольших сетей. Число элементов в системе растет очень быстро с ростом числа узлов и ветвей (примерно как N²M), по­этому составление такой системы уравнений для сети, содержа­щей несколько десятков узлов, практически невозможно даже с использованием ЭВМ.

Это привело к разработке итерационных методов расчета, не связанных

составлением полной системы уравнений. В этих работах определение

вероятностей потерь на ветвях осуществля­ется в два этапа. На первом этапе

последовательно для каждой пары узлов определяются и суммируются все доли

нагрузки на каждую ветвь в соответствии с заданным планом распределении

потоков:

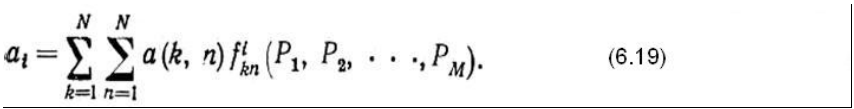
На втором этапе по полученным величинам нагрузок определя­ются вероятности потерь на ветвях.

При расчете итерационным методом можно основываться на распределении нагрузки между каждой парой узлов, как по де­реву путей, так и по матрице маршрутов

• Анализ сетей связи с пакетной коммутацией

При анализе сетей связи ЭВМ, в которых используется пакетная коммутация, в первую очередь не­обходимо оценить пропускную способность сети, т. е. такую ско­рость передачи сообщений, которая может быть получена при связи между двумя ЭВМ или абонентским пунктом и ЭВМ. Так как ЭВМ и абонентский пункт связаны с опорным узлом (ОУ) сети связи абонентской линией, ско­рость обмена определяется в первую очередь ее пропускной спо­собностью. Однако скорость обмена зависит также от пропускной способности сети связи. Эта сеть обеспечивает передачу сообщений от ОУ, в который включен абонент, передающий это сообщение к ОУ, в который включена линия его потребителя.

Кроме пропускной способности, при анализе такой сети связи ЭВМ необходимо оценить также задержки (максимальные и иног­да минимальные) передачи сообщений в сети. Эти задержки могут воз­никнуть из-за конечного времени распространения сигналов по линиям связи, очереди на передачу сообщений на оконечных и всех транзитных узлах и затрат времени на обработку сообщений или пакетов в ОУ сети.

Зная максимальную пропускную способность сети B_ij между исходящим и входящим ОУ и объем сообщения φ_ij можно оце­нить минимальное время Т'_ij передачи сообщения с ОУ_i- на ОУ_j без учета его задержки в сети: T^/_ij = φ_ij /B_ij. Вычислив затем ми­нимальную задержку T "_ij в сети при передаче этого сообщения, можно оценить общее минимальное время передачи сообщения с ОУ_i, на ОУ_j: Ti = T '_ij + T "_ij. Зная время передачи сообщения по АЛ от А6а на ОУг (Tа.исх) и с ОУ_;- к Аб_в(Tа.вх), получим оценку общего времени передачи сообщения от Аб_A к Аб_В :

Т_АВ= Та.исх +Т _ij,+Tа,вх. (6.20)

Рассмотрим решение этой основной задачи анализа сети связи ЭВМ методами теории потоков, некоторые элементы которой были рассмотрены в предыдущем параграфе. Вначале рассмотрим реше­ние задачи по определению пропускной способности сети. При этом вычислим максимальную пропускную способность сети между ОУ_i и ОУ_j , для чего предположим, что по сети передается только один поток φ_ij, т. е. рассмотрим двухполюсную сеть связи.

Пусть, например, задана сеть связи ЭВМ, изображенная на рис., где зачерненные ОУ являются исходящим узлом(узел А) и входящим узлом(узел D). Для примера примем φ_AD =9,6 кбит.

Рис. 6.5 Схема анализируемой сети. Веса элементов сети представляют время задержки.

Для данной сети матрица емкостей ветвей D, задающая пропускные способности ветвей вей в виде допустимой скорости передачи по ним в кбит/с, имеет вид

Всвязи с тем, что сеть неориентированная, всего можно обра­зовать 31 сечение. Из них наименьшими являются сеченияS₁=S₂=3,2. Поэтому емкость минимального сечения S_mиh= 3,2 кбит/с. Следовательно, минимальное время передачи сообще­ния (потока) φ_AD между ОУ_Аи ОУ_В без учета его задержки в сети составит

Для вычисления величины задержки сообщения (или пакета) в сети будем считать, что в матрице длин ветвей, задающей в данном случае время передачи по ветвям сети, учтены время рас­пространения сигналов по линии, задержка сообщения (пакета) на ОУ из-за очереди на передачу, а также время его обработки на ОУ.

В связи с тем, что задержка сообщения (пакета) на ОУ отнесена к исходящим из ОУ ветвям, в матрице длин ветвей эле­мент 1 _ij = 0. Для вычисления минимальной задержки в сети при передаче сообщения с ОУ_Аи ОУ_В определим длину кратчайших путей между различными узлами в виде минимальной задержки в секундах с учетом матрицы . Полученные данные представим в матрице D.

Как видно из матрицы D, минимальная задержка в сети при передаче сообщения с ОУ_А и ОУ_D составит T"_Ad=6 с. Общее минимальное время передачи сообщения от абонента Аб₁ к Аб₂ , без учета времени передачи по абонент­ским линиям, составит T₁₂=T^/_AD+T"_AD=3 + 6=9 с.

Полученное минимальное время передачи является лишь ниж­ней оценкой, вообще говоря, достижимой, так как при ее вычисле­нии не учитываются истинные маршруты передачи сообщения (пакетов). Вычисление реального значения времени передачи сооб­щения в сложной многополюсной сети, когда по сети передается одновременно множество сообщений и для их передачи исполь­зуются различные маршруты, связано со значительными труднос­тями. В связи с этим при анализе сложных сетей связи ЭВМ ис­пользуются методы статистического моделирования на ЭВМ.