
- •О.И.Тутынина
- •Пояснительная записка
- •Методические материалы к самостоятельной работе
- •Самостоятельная работа № 6. Тема: Векторное и смешанное произведения векторов
- •Самостоятельная работа № 7. Тема: Способы задания прямой на плоскости
- •Самостоятельная работа № 8. Тема: Способы задания плоскости
- •Самостоятельная работа № 9. Тема: Способы задания прямой в пространстве
- •Самостоятельная работа № 10. Тема: Взаимная ориентация прямой и плоскости
- •Самостоятельная работа № 11. Тема: Преобразования кривых второго порядка
- •Список рекомендуемой литературы
Самостоятельная работа № 10. Тема: Взаимная ориентация прямой и плоскости
Найти угол между прямой
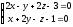 и плоскостью
и плоскостью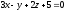 .
.Найти точку пересечения прямой
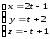 и
плоскости
и
плоскости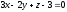 .
.Найти канонические уравнения прямой, заданной общими уравнениями
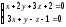 Написать канонические уравнения прямой,
проходящей через точку М(4,-2,1) параллельно
прямой
Написать канонические уравнения прямой,
проходящей через точку М(4,-2,1) параллельно
прямой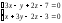
Найти угол между прямой
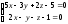 и плоскостью
и плоскостью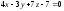 .
.Найти угол между прямой
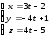 и плоскостью
и плоскостью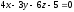 .
.Найти угол между прямой
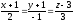 и плоскостью
и плоскостью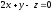 .
.Найти точку пересечения прямой
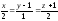 и плоскости
и плоскости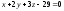 .
.Найти точку пересечения прямой
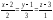 с плоскостью 2х+3у+z=0.
с плоскостью 2х+3у+z=0.
Найти уравнение плоскости, проходящей через прямую
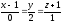 ,
перпендикулярно плоскости
,
перпендикулярно плоскости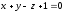 .
.Написать уравнение плоскости, проходящей через две параллельные прямые
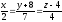 и
и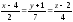
Найти угол между прямой
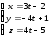 и плоскостью
и плоскостью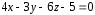 .
.Найти уравнение плоскости, проходящей через точку М(1,-2,-2) и прямую
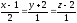 .
.Найти уравнение плоскости, проходящей через точку М(3,-2,-2) перпендикулярно прямой
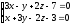 .
.Найти уравнение плоскости, проходящей через точку М(2,-3,0) и прямую
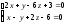 .
.Написать уравнение плоскости, проходящей через две параллельные прямые
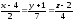 и
и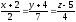
Найти уравнение плоскости, проходящей через точку прямую
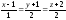 перпендикулярно плоскости 2х+3у-z-4=0.
перпендикулярно плоскости 2х+3у-z-4=0.
Найти уравнение плоскости, проходящей через точку М(1,2,-1) и прямую
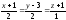 .
.
Самостоятельная работа № 11. Тема: Преобразования кривых второго порядка
Составить уравнение параболы с вершиной в начале координат и фокусом в точке
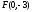 .
.Точка (0,4) является центром эллипса, касающегося обеих координатных осей. Составить каноническое уравнение эллипса, если его оси симметрии параллельны координатным осям.
Привести уравнение гиперболы
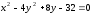 к
каноническому виду. Найти оси, вершины,
фокусы, эксцентриситет и асимптоты
гиперболы.
к
каноническому виду. Найти оси, вершины,
фокусы, эксцентриситет и асимптоты
гиперболы.Привести уравнение эллипса
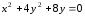 к каноническому виду. Найти оси, вершины
и эксцентриситет эллипса.
к каноническому виду. Найти оси, вершины
и эксцентриситет эллипса.Составить каноническое уравнение гиперболы, асимптоты которой
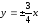 ,
а расстояние между фокусами равно 30.
,
а расстояние между фокусами равно 30.Привести уравнение параболы
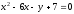 к
каноническому виду. Определить координаты
ее вершины и фокуса.
к
каноническому виду. Определить координаты
ее вершины и фокуса.Составить каноническое уравнение гиперболы, если уравнения ее асимптот
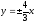 и с=10.
и с=10.Составить каноническое уравнение параболы, симметричной оси х, если она проходит через точку А(-3,-3), ее вершина находится в начале координат.
Привести уравнение эллипса
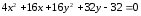 к каноническому виду. Найти оси, вершины
и эксцентриситет эллипса.
к каноническому виду. Найти оси, вершины
и эксцентриситет эллипса.Привести уравнение параболы
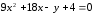 к
каноническому виду. Определить координаты
ее вершины и фокуса.
к
каноническому виду. Определить координаты
ее вершины и фокуса.Привести уравнение эллипса
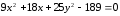 к
каноническому виду. Найти оси, вершины
и эксцентриситет эллипса.
к
каноническому виду. Найти оси, вершины
и эксцентриситет эллипса.Привести уравнение гиперболы
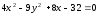 к
каноническому виду. Найти оси, вершины,
фокусы, эксцентриситет и асимптоты
гиперболы.
к
каноническому виду. Найти оси, вершины,
фокусы, эксцентриситет и асимптоты
гиперболы.Привести уравнение параболы
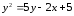 к
каноническому виду. Определить координаты
ее вершины и фокуса.
к
каноническому виду. Определить координаты
ее вершины и фокуса.Привести уравнение гиперболы
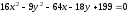 к
каноническому виду. Найти оси, вершины,
фокусы, эксцентриситет и асимптоты
гиперболы.
к
каноническому виду. Найти оси, вершины,
фокусы, эксцентриситет и асимптоты
гиперболы.Даны две точки эллипса А(3,5) и В(6,3). Найти каноническое уравнение эллипса.
Привести уравнение эллипса
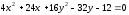 к
каноническому виду. Найти оси, вершины
и эксцентриситет эллипса.
к
каноническому виду. Найти оси, вершины
и эксцентриситет эллипса.Привести уравнение параболы
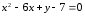 к
каноническому виду. Определить координаты
ее вершины и фокуса.
к
каноническому виду. Определить координаты
ее вершины и фокуса.Привести уравнение гиперболы
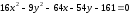 к
каноническому виду. Найти оси, вершины,
фокусы, эксцентриситет и асимптоты
гиперболы.
к
каноническому виду. Найти оси, вершины,
фокусы, эксцентриситет и асимптоты
гиперболы.
