1.2 Примеры задач с решениями

1.2.1 Исходные данные: Индукция в сердечнике В_m =1,0 Тл, число витков в первичной обмотке W₁ =1000 витков, напряжение U₁ =100 В меандр с частотой 1кГц.

Определите площадь поперечного сечения магнитопровода трансформатора.

Решение: Воспользуемся уравнением 1.3 трансформаторной ЭДС для прямоугольной формы напряжения: 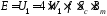. Откуда находим

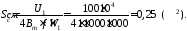
1.2.2 Исходные данные: Максимальная индукция в сердечнике из феррита равна В_m =0,38 Тл при напряженности Н_c=25А/м (рисунок 1.5), число витков первичной обмотки W =800, поперечное сечение магнитопровода S_с =0,19 см², средняя длина магнитной силовой линии ,частота преобразования f=10 кГц,.

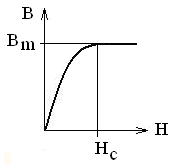
Рисунок 1.5 – Основная кривая намагничивания сердечника

Определите предельные значения тока холостого хода I_1ХХ , напряжения U₁ и изобразите график зависимости .

Решение: из уравнения трансформаторной ЭДС следует:

. Предельное значение тока холостого хода –

.

Учитывая характер изменения и то, что, а , график зависимости намагничивающего тока трансформатора от приложенного напряжения имеет примерно квадратичный характер (рисунок 1.6).

Рисунок 1.6 – Зависимость намагничивающего тока трансформатора от приложенного напряжения

1.2.3 Исходные данные: Зависимость магнитного потока от времени Ф(t) показана на рисунке 1.7.

Рисунок 1.7 – Зависимость магнитного потока от времени Ф(t)

Изобразите зависимость ЭДС от времени.

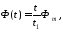
Решение: Учитывая закон электромагнитной индукции , определим Е(t) раздельно по участкам. На участке [0…t₁] функция линейна и скорость (производная) постоянн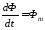а: . Тогда 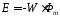. Научастке [t₁…t₂] поэтому . На интервале [t₂…t₃], повторяется участок [0…t₁], но с другим знаком. На участке [t₃…t₄] имеет место гармонический закон изменения потока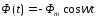, поэтомуполучаем ортогональную функцию (). Результирующая зависимость Е(t) изображена на рисунке 1.8.

Рисунок 1.8 – Зависимость ЭДС от времени

1.2.4 Исходные данные: ЭДС обмотки трансформатора изменяется во времени, как показано на рисунке 1.9.

Рисунок 1.9 – ЭДС от времени

Изобразите временную зависимость магнитного потока Ф(t).

Решение: Согласно закону электромагнитной индукции магнитный поток есть интеграл от ЭДС. Рассмотрим участок [0…t₁]. По правилам интегрирования: 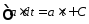для конечных приращенийнаходим: .На участке [t₁…t₂] с учётом изменения знака ЭДС, график будет возрастать . Таким образом, кривая магнитного потока Ф(t) имеет вид, как показано на рисунке 1.10.

Рисунок 1.10 – Временная зависимость магнитного потока

1.2.5 Исходные данные: В однофазном трансформаторе при КПД=0,95 и коэффициенте нагрузки , выходная мощность равнаP₂ =190 Вт.

Определите потери в обмотках.

Решение: КПД трансформатора . При оптимальном коэффициенте нагрузки, как следует из рисунка 1.11 .

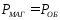Рисунок 1.11 – Зависимости потерь в обмотках, потерь в магнитопроводе и КПД откоэффициента нагрузки

Следовательно,

1.2.6 Исходные данные: В результате проведения опыта короткого замыкания найдено Rкз = 10 Ом для трансформатора с отношением W1/W2=5.

Определите сопротивления потерь первичной и вторичной обмоток.

Решение: Схема замещения трансформатора в опыте КЗ имеет вид, показанный на рисунке 1.12.

Рисунок 1.12 – Схема замещения трансформатора в опыте КЗ

Из определения коэффициента трансформации следует, что

В оптимальном трансформаторе имеет место: Следовательно, .

1.2.7 Исходные данные: В схеме замещения трансформатора (рисунок 1.13) U_1ном=141 В, U_к=10%, ,.

Определите номинальный ток в первичной цепи трансформатора.

Рисунок 1.13 – Схема замещения трансформатора

Решение: Определим внутреннее сопротивление трансформатора:

, ,.

В опыте КЗ на вход подаётся пониженное напряжение: . Тогда номинальный ток равен .

1.2.8 Исходные данные: Трансформатор выполнен на броневом сердечнике (рисунок 1.14). Все обмотки равны W₁=W₂=W₃. К обмотке W₁ подведено напряжение U₁=100В.

Определите напряжения U₂ и U₃._.

Рисунок 1.14 – Трансформатор

Решение: В сердечнике трансформатора основной магнитный поток разделяется на два потока, которые пронизывают обмотки W₂ и W₃. Из уравнения трансформаторной ЭДС: 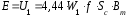следует, что основной магнитный поток прямо пропорционален Е, следовательно, напряжение на обмоткахU₂ = U₃ =50 В.

1.2.9 Исходные данные: В стержневой однофазный трансформатор (рисунок 1.15) вводится магнитный шунт.

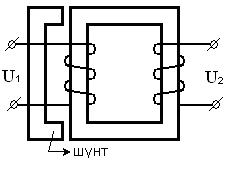
Рисунок 1.15 – Магнитный шунт

Определите как изменится выходное напряжение трансформатора на холостом ходу (U₂) при введении магнитного шунта.

Решение: Вследствие введения магнитного шунта, появляется ещё один путь (см. рисунок 1.16) для магнитного потока, что приведёт к уменьшению потока Ф ₀ и уменьшению напряжения U₂.

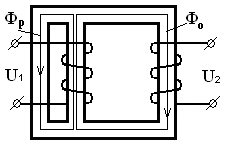
Рисунок 1.16 – Влияние магнитного шунта

1.2.10 Исходные данные: Потери в магнитопроводе трансформатора составляют Pмаг = 10 Вт; соотношение витков W1/W2= 1; активные сопротивления обмоток r₁ = r₂ = 0,2 Ом.

Определите при каком токе нагрузки I₂ КПД трансформатора будет максимальным?

Решени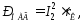е: где . Тогда.

1.2.11 Исходные данные: В опыте холостого хода трансформатора U_1ХХ=220В; I_1ХХ=0,4A; P_МАГ =16Вт.

Определите активное сопротивление цепи намагничивания в схеме замещения трансформатора.

Решение: В опыте холостого хода схема замещения трансформатора имеет вид (рисунок 1.17):

Рисунок 1.17 – Схема замещения трансформатора в опыте ХХ

Тогда .

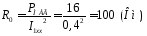1.2.12 Исходные данные: В трансформаторе при питании от сети с напряжением 220 В и частотой сети f=50 Гц потери в магнитопроводе составляют Р_маг=20 Вт.

Определите потери в магнитопроводе, если этот трансформатор включить в сеть с частотой 400 Гц и напряжением 110 В (зависимость потерь от частоты принять квадратичной).

Решение: Магнитная индукция пропорциональна напряжению, а потери зависят от индукции и частоты . Следовательно,

1.2.13 Исходные данные: Первичная обмотка трёхфазного трансформатора соединена звездой (рисунок 1.18).

Рисунок 1.18 – Соединение обмоток звездой и векторная диаграмма напряжений

Определите во сколько раз изменятся потери в магнитопроводе, если первичную обмотку трёхфазного трансформатора переключить на треугольник.

Решение: При соединении обмоток звездой линейные напряжения (U_л) больше фазных (Uф) в раз.При соединение в “треугольник” (рисунок 1.19): U_л = U_ф.

Рисунок 1.19 – Схема соединения обмоток треугольником и векторная диаграмма напряжений

Потери зависят от индукции и частоты . При переходе на соединение треугольником напряжение, прикладываемое к фазной обмотке увеличивается в раз, что приведёт к увеличению магнитной индукции враз, а потери возрастут в 3 раза.