ЧИСЛЕННЫЕ МЕТОДЫ МАТЕМАТИЧЕСКОГО МОДЕЛИРОВАНИЯ.

(Лекции темы:4-8)

Тема 4: применение интерполяции

§1. Обратное интерполирование

С помощью обратной интерполяции можно решать нелинейные уравнения вида:

f(x)=a ( f(x)=0 ).

Идея обратной интерполяции:

Пусть в точках x₀, х₁, …, х_п заданы значения

у₀=f(x₀), у₁=f(х₁)…, у_п=f(х_п)

Предположим, что функция f на участке x₀, х₁, …, х_п монотонна – для определенности - монотонно возрастает, тогда существует обратная функция f ^-1 . Определим функцию f ^–1(y) и найдем значение функции f(x_i)=y_i в точке a – это и будет решением нелинейного уравнения f(x)=a. Таким образом получена обычная задача интерполяции. Для решения этой задачи используется какой-либо метод интерполяции, например, интерполяция многочленами: метод Лагранжа.

Х0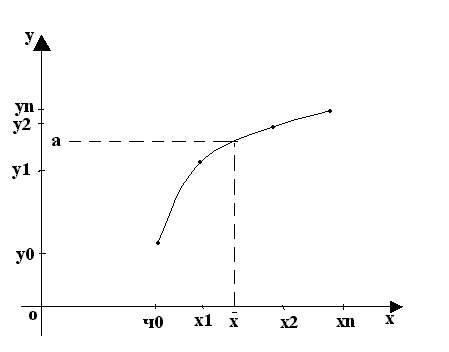

Пример:

ху

10. 3

10. 7

10. 11

10. 17

у(х)=10 (это ~ 16,5)

проводим интерполяционный многочлен через точки у₀, у₁, у₂, у₃ принимающие в этих точках значения указанные в таблице.

чтобы найти корень, необходимо найти Р₃(10)=16,641 – это решение уравнения.

§2.Численное дифференцирование функций

П.0 Постановка задачи численного дифференцирования

В узлах х₀, х₁,…, х_п заданы значения функции у₀=f(х₀)…у_п=f(х_п)

Задача:

Найти производную f’ и производные высших порядков от функции f в любой заданной точке х.

П.1 Формула численного дифференцирования (ЧД)

Общая идея ЧД: Неизвестную функцию f заменить на интерполирующую функцию g ( то есть на функцию g: g(x_i)=y_i и заменить f^’(x) на g^’(x) ) . В качестве интерполирующей функции рассмотрим только интерполяционный многочлен.

Вдальнейшем будем считать, что узлы х_i=х₀+iх, i=0, n равностоящие с шагом х. Рассмотрим первый интерполяционный многочлен Ньютона:

где: ,

Как и в первой интерполяционной формуле Ньютона суммирование в формуле (4.2) можно прервать. При этом, если в формуле взято k слагаемых (не считая 0), то будет получена производная от интерполяционного многочлена, интерполирующая функцию не во всех точках, а только в крайних левых (k+1) точках. Продифференцировав формулу (4.2) по х еще один раз, получаем:

(4.3)

Если в (4.3) взять первые k слагаемых, то получим вторую производную от интерполяционного многочлена, проходящего через (k+2) точки х₀, х₁,…, х_к+1.

Часто необходимо найти у’ и у”.

(4.4) доказательство 4 балла

(4.5)

На практике удобнее дифференцировать не первый интерполяционный многочлен Ньютона ( он односторонний ), а центральную формулу Стирлинга, так как узлы интерполяции располагаются симметрично относительно начальной точки x₀ (см т.3 пар.1 п.4). Выпишем первые два слагаемых:

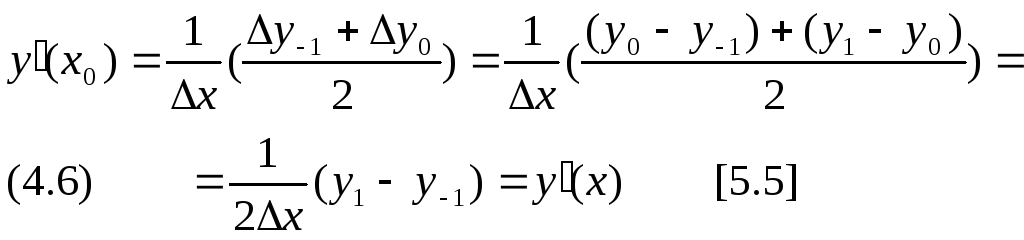
Формула (4.6) точнее, чем (4.2) с одним слагаемым. Аналогично на основе интерполяционного многочлена Стирлинга могут быть получены формулы:

эта формула будет получена, если взять в интерполяционном многочлен Стирлинга первые три слагаемых и х=х₀ (т.е. q=0) :

эта формула будет получена при двукратном дифференцировании первых трех слагаемых интерполяционного многочлен Стирлинга при х=х₀.

П.2 Оценка погрешностей численного дифференцирования

При численном дифференцировании, как и при интерполяции, возникает два типа погрешностей. Погрешность усечения – из-за замены функции на ее интерполирующий многочлен и ее производной на производную от интерполяционного многочлена. Погрешность округления – из-за того, что значение у_i известны не точно, а с некоторой погрешностью . Оценим погрешность усечения.

Теорема 4.1

Погрешность усечения при численном дифференцировании (при использовании производной от первой интерполяционной формулы Ньютона – формула (4.2)),

при суммировании k-слагаемых имеет следующую оценку:

(погрешность усечения можно оценить только в узлах интерполяции)

где   [х₀,х_к].

Доказательство:

Вспомним оценку остаточного члена первой интерполяционной формулы Ньютона

Дифференцируем по х:

Комментарий:

При доказательстве теоремы был использован неявно тот факт, что функция (x)- дифференцируемая.

Замечание 4.2

Погрешность усечения численного дифференцирования из теоремы 4.1 удобнее оценивать следующим образом:

, где

если трудно оценить значение (к+1) производной от функции f, то f заменяют на конечную разность (к+1) порядка.

Погрешности усечения формул (4.6) и (4.7) оцениваются следующим образом:

Для (4.6) 

Для (4.7) 

Для (4.8) →

где ,

У

казания:

Для доказательства этих оценок необходимо продифференцировать соответственно r₂(х) r₄(х) в точках х=х₁ и х₂ соответственно. После чего сдвинуть интервалы влево [х₀,х₂] сдвинуть до  [х_-1,х₁], [х₀,х₄]  [х_-2,х₂].

Погрешности округления:

Оценим погрешности округления формул (4.7) и (4.6).

Очевидно, они равны и

Погрешность усечения при уменьшении х уменьшается и при х0 она тоже стремиться к нулю. Погрешность округления, напротив, увеличивается, а при х0, она  .

у

Δх

Суммарн.

Погрешность усеч.

Погрешность округлен.

Δх

Шаг не следует брать слишком большой, чтобы погрешность усечения не была велика и нельзя слишком маленький, чтобы не была велика погрешность округления.

Найдем оптимальное для формул (4.6) (4.7) .

Для (4.6): суммарная погрешность:

Находим производную по и =

для (4.7): суммарная погрешность равна:

Без вывода приведем погрешности усечения, округления формулы (4.8).

Для (4.8): погрешность усечения , где

погрешность округления .

Пример (численного дифференцирования):

х	У	у	2у	3у
50	1,6990	0,0414	-0,0036	0,0005
55	1,7404	0,0378	-0,0031
60	1,7782	0,0347
65	1,8129

По формуле из теоремы 4:

у’(50)=1/5(0,0414-1/2(-0,0076)+1/3(0,0005))=0,00872

Погрешность усечения при этом (по теореме 4.1 и замечание 4.10) может быть оценена по формулам 4.10 и 4.11. При использовании 4.10 надо найти четвертую производную lg, а при использовании 4.11 надо найти четвертую разность от lg.

Если же будем искать ⁴(у), то потребуется еще одно значение функции и вычисление будет необходимо произвести с большей точностью (из-за быстрого уменьшения конечной разности и быстрого накапливания погрешности)  используем 4.10.

r₃(50), где , можно и

достигается при х=50 и равно 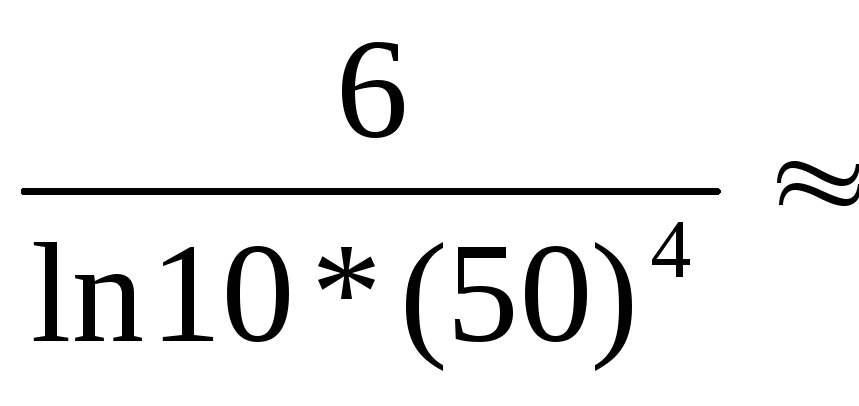и получаем

Таблица для погрешностей центральных формул.

4.6
4.7				15/8
4.8				2/

Комментарий к погрешности усеченной формулы Симпсона:

При использовании формулы Симпсона происходит интерполяция по трем узлам, а потому следует ожидать, что формула Симпсона будет точна для многочлена до второй степени включительно.

На самом деле, как мы видели из формулы (4.18), формула Симпсона будет точна для многочленов до третьей степени включительно, это явление имеет место при всех четных n.

В общем случае, если n=2k+1 – нечетное, то соответствующая квадратурная формула будет точна для многочленов до степени 2k включительно, если же n=2k – четное, то соответствующая квадратурная функция будет точна до степени n+1 включительно.