10.8 Программа синтез антенной решетки по заданному уровню боковых лепестков
КПД
антенны.
Частота
на которой проектируется антенна.
Частота
на которой расчитываются
характеристики
антенны.
Общая
длина антенны [m].
Уровень
Бок.Л. [dB].
Направление
ГЛ. излучения [град.].
Определение
шага решетки (d) и
числа
излучателей (Ng).
Определение
параметра формы ДН (zo) и амплитуды токов
в излучателях (Jg) .
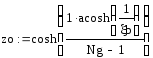
Рис.10.17 Токи в излучателях
Расчет дн антенны по найденному распределению питающих токов.
Рис.10.18 ДН антенны
Определяем
коэфф. пропорциональности (δ) и
относительную излучаемую мощность
(Vg) .
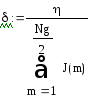
Определяем
коэфф. связи излучателей с питающей
линией (kf) .
Рис.10.19 Связь излучателей с линией
Определение
относительной мощности через коэфф.
связи излучателей с питающей линией
(обратная задача.
Рис.10.20 Относительная мощность излучения
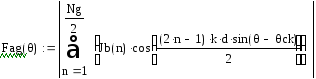
Рис. 10.21 ДН спроектированной антенны в разах и относительных единицах
Расчет КИП антенны.
Глава 11. О МОДЕЛИРОВАНИИ КАНАЛА СВЯЗИ
11.1 Применение метода малых отклонений при моделировании каналов
Развитие модельного эксперимента при разработке и исследованиях телекоммуникационных систем (ТС) обусловлено как сложностью моделирования систем, так и сложностью создания модели канала связи, т.е. в таких исследованиях оценка качественных показателей телекоммуникационной системы (ее модели) оценивается на модели канала.
В процессе модельного эксперимента обычно производится оценка помехоустойчивости системы связи, сравнительная оценка эффективности различных режимов ее работы и работы отдельных функциональных элементов, а также сравнение различных систем между собой.
Для техники телекоммуникаций актуальным является передача и прием дискретных сообщений. Развитие теории и техники передачи сообщений неразрывно связано с совершенствованием модели канала. Применение метода статистических испытаний (Монте-Карло) при моделировании канала с переменными параметрами позволяет проводить исследования процесса передачи информации на современных компьютерах, в том числе и на персональных (ПК).
В процессе модельного эксперимента производится оценка помехоустойчивости систем передачи дискретной информации (СПДИ) или их моделей, сравнительная оценка эффективности различных режимов ее работы и работы отдельных функциональных элементов, а также сравнение различных систем (их моделей) между собой.
Оценка помехоустойчивости СПДИ в процесс модельного эксперимента в значительной степени будет зависеть от параметров и характеристик модели канала и точности их имитации. Для получения достоверных оценок помехоустойчивости СПДИ требуется достаточно точное моделирование характеристик и параметров заданной модели.
Такая задача может быть решена на основе определения коэффициентов влияния параметров канала на точность измерения помехоустойчивости СПДИ и оценки допустимых расхождений одномерных законов распределения огибающей сигнала на выходе заданного канала и его модели [].
При моделировании каналов со случайными параметрами необходимо:
обосновать количественную меру адекватности модели и канала;
классифицировать погрешности, возникающие при измерении помехоустойчивости СПДИ на моделях каналов;
исследовать влияние погрешностей моделирования параметров;
определить требования к допустимому расхождению одномерных законов распределения параметров сигнала на выходе канала и его модели.
Ниже рассматривается пример применения метода анализа точности моделирования канала на основе теории чувствительности (метод малых отклонений).
Для получения оценок погрешностей средней вероятности ошибки (ОСВО) на модели канала, обусловленных погрешностью моделирования одномерной функции распределения огибающей, используется непараметрический критерий согласия числовая мера различия эмпирической и гипотетической функций распределения.
В качестве количественной меры адекватности модели и канала используется относительная разность средней вероятности ошибки СПДИ, которая полностью определяет достоверность получаемых оценок помехоустойчивости для любых систем и каналов.
Будем отождествлять смоделированный канал с исходным (гипотетическим), если одинаковы значения получаемой средней вероятности ошибки для оптимальной СПДИ (или ее модели) на модели и исходном (гипотетическом) канале.
При моделировании канала требуемая точность моделирования параметров определяется для оптимальных СПДИ, поскольку обычно неизвестны аналитические выражения для средней вероятности ошибки исследуемых реальных систем. Целесообразность такого подхода следует и из того, что при синтезе СПДИ всегда стремятся приблизить ее качественные показатели к оптимальным.