10.4 Синтез излучателей методом интеграла Фурье

В соответствии с формулой (10.6) множитель направленности линейного излучателя является преобразованием Фурье от функции распределения токавдоль излучателя. Следовательно, задавшись требуемой характеристикой направленности,, можно с помощью обратного преобразования Фурье найти распределение возбуждения:

(10.16)

Однако, требуемая характеристика известна только в пределах действительных углов, а интеграл берется по бесконечному интервалу.

Можно задаться конкретной длиной излучателя и методами теории функций комплексного переменного построить аналитическое продолжение функции 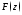на всю вещественную ось (z). Подстановка этой функции в выражение (10.16) позволяет найти распределение возбуждения вдоль излучателя и дает точное воспроизведение ДН. Но полученное решение может оказаться неустойчивым.

Для обеспечения корректности решения задачи можно потребовать, чтобы заданная ДН была равна нулю вне области видимост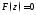и:при, и интегрирование (10.16) выполнить в пределах.

Распределение возбуждения теперь будет определяться так:

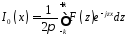(10.17)

Так как функция F(z) не принадлежит к классу целых функций то распределение возбуждения будет отличным от нуля по всей оси (x), поэтому необходимо использовать усеченное распределение I(x), ограниченное только пределами излучателя . Характеристика направленности в этом случае будет определяться выражением:

,

и будет отличаться от заданной функции F(z).

Можно показать, что эти отличия, в большинстве случаев, будут незначительные, если характеристику направленности определять через возбуждение найденное по формуле (10.17):

(10.18)

Найденное решение является наилучшим среднеквадратичным приближением к заданной характеристике направленности. Именно такой способ решения задачи и получил название метода интеграла Фурье.

10.5 Описание программ синтеза линейного излучателя в средеMathcad

Программа синтеза линейного излучателя методом парциальных диаграмм!

Рабочая частота!

Задаем число излучателей и шаг между ними!

Формируем требуемую ДН антенны!

Рис.10.2 Требуемая ДН

Определение значений угловой переменной u=ksin() в характерных точках ДН антенны!

Формируем ДН в области реальных углов !

Рис.10.3 Парциальная ДН

Рис. 10.4 Диаграмма направленности

Определяем число отсчетов (выборок по u)! и определяем значение парциалов (коэффициентов Котельникова) в этих точках! Построение фукция распределения возбуждения рядом Фурье!

Рис.10.5 Токи в излучателях

Рис.10.6 Фаза токов

Расчет ХН антенны через парциальные ДН и по найденному возбуждению!

Рис.10.7 Синтез ДН

Рис.10.8 Синтез ДН

Определяем КИП излучателя!