10.2 Характеристика направленности как целевая функция

Прежде всего, следует отметить, что соотношение (10.4) фактически представляет собой преобразование Фурье от функции возбуждения везде, где. В этом случае характеристика направленности антенны приобретает вид:

(10.6)

Чтобы функция допускала преобразование (10.6), она должна интегрироваться с квадратом на интервале (- ∞,+∞), давать полную мощность, и иметь конечное число минимумов и максимумов в пределах любого интервала. Эти же ограничения справедливы и для функции, для которой обратное преобразование Фурье будет таким:

(10.7)

Характеристика направленности , или функция преобразования Фурье имеет ограниченный спектр, в силу того, что функция возбуждаетсяопределена только на интервале, что существенно сужает класс функций. Причем эти целые функции представляют собой на комплексной плоскости (z),в ограниченной области, аналитические функции конечной степени, не превосходящей . Числоназывается степенью или типом функции и определяется как.

Примером целой функции может быть функция вида, здесь, или.

Таким образом, множитель направленности линейного излучателя длиной является целой функцией степени, не превышающей значения. Это же утверждение справедливо для более сложных систем. В принципе, с помощью линейной системы длинойможно реализовывать множитель направленности в виде любой наперед заданной непрерывной функции.

10.3 Синтез линейного излучателя методом парциальных диаграмм направленности

Пусть распределение возбуждения в линейном излучателе имеет вид

, (10.8)

ряда из некоторых известных функций . Подставим этот ряд в выражение для характеристики направленности антенны (10.6)

(10.9)

Здесь зависящая от текущего номера (i) функция

,

представляет собой парциальную диаграмму направленности, соответствующую функции распределения возбуждения 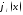. Теперь заданная функция диаграммы направленностиможет быть аппроксимирована с помощью ряда (10.9). Для этого потребуется вычислить необходимые коэффициенты () и затем найти функцию распределения возбуждения излучателя с помощью формулы (10.8). Все эти действия и представляют сущность метода синтеза ДН с помощью парциальных диаграмм направленности.

Наиболее просто этот метод реализуется при среднеквадратичном приближении, а в качестве системы функций берутся любые полные функции, удовлетворяющие условию ортогональности на интервале.

.

В этом случае коэффициенты аппроксимации [] могут быть вычислены по заданной ДНкак коэффициенты Фурье разложения:

(10.10)

Функция является преобразованием Фурье от функции распределения, отличным от нуля на интервале. Поэтому функциибудут представлять собой целые функции степени, не превышающей.

В качестве парциальных ДН и в качестве соответствующих гармоник возбуждения в антенной технике, широко используется следующая система парциальных диаграмм:

(10.11)

Эти функции образуют ортогональную систему диаграмм и ортогональную систему распределения возбуждения на интервале .

Выразим заданную функцию диаграммы направленности в виде ряда:

(10.12)

Фактически ряд (10.12) представляет собой интерполяционный ряд Котельникова для целых функций степени, не превышающей () на всей оси (z).

Особенностью системы парциальных диаграмм (10.11) является то, что в точках , только одна диаграмма с номеромимеет максимум, а все остальные парциальные диаграммы в этой точке равны нулю. В силу этого, неизвестные коэффициенты разложения (), входящие в формулу (10.12), будут являться равноотстоящими выборками заданной функции направленности:

, (10.13)

Для определения всех коэффициентов () функциядолжна быть известна на всей оси (z). Тут возможно два подхода определения функции:

• функцию аналитически продолжена на всю осьz, как целая функция степени не выше , что ведет к точному воспроизведению направленности, но решение может оказаться некорректным;

• заданная функция приравнивается к нулю вне интервале.

Но, это дает возможность найти только первые коэффициенты ряда Котельникова и синтезируемая диаграмма направленности будет определяться так:

, (10.14)

где , аN равна целому числу отношения(L/λ), f(idz) = a_i.

Необходимое распределение возбуждения, для получения синтезируемой ДН, определяется конечным рядом Фурье:

(10.15)

Решение задачи в виде уравнений (10.14), (10.15) будет удовлетворять условию корректности, однако полученная ДН будет совпадать с заданной функцией только в точках отсчета.