9.9 Реализация звеньев первого порядка

Передаточная функция фильтра нижних частот первого порядка в общем случае определяется выражением (9.22). Фильтр с такой передаточной функцией может быть реализован, если в цепи обратной связи операционного усилителя использовать пассивный RC– фильтр первого порядка (рис. 9.47).

Рис. 9.47Активный фильтр нижних частот первого порядка

Для этого звена используя метод узловых напряжений можно записать систему для передаточной функции:

Полагая, что собственный коэффициент ОУ μ→ ∞ и решая эту систему относительно коэффициента передачи звена H₁(p) =U₂/U₁получим:

(9.23)

Сравнивая выражения (9.22) и (9.23) получаем: а₁= 1;K_o= –R₂/R₁;b₂= 1;b₁=C₁R₂и частота среза фильтра.

Задавшись коэффициентом передачи постоянного сигнала К_o, при известной ω_сможно найти элементы схемы:

C₁~;;

Можно построить ФНЧ по неинвертирующему входу (Рис. 9.48)

Рис. 9.48Фильтр НЧ первого порядка

Напряжение на выходе будет определяться как U₂= μ (U₁-U₃) и тогда выражение для коэффициента передачи такого звена будет:

Но, при таком построении фильтра на высоких частотах будет давать коэффициент пердачи Н(р) ≈ 1. Поэтому, при неинвертирующем включении чаще используют схему приведенную на рисунке 9.49.

Рис. 9.49ФНЧ первого порядка

Используя метод узловых напряжений для узла 3 получим:

Решая эту систему относительно U₂/U₁с учетом того, что μ→ ∞ получаем:

(9.24)

Сравнивая выражение (9.24) и (9.22) заключаем: а₁=1; К₀= 1+R₃/R₂ ;b₂= 1; К₁ = 1;b₁=C₁R₁. Элементы рассчитываются следующим образом выбирается С₁ ≈ 10/f_c[мкФ];;;;. При К₀= 1,, а.

Для получения передаточной функции фильтра верхних частот первого порядка, необходимо в выражении (9.22) параметр pзаменить на 1/p. Тогда получим:

(9.25)

Схема активного фильтра верхних частот на инвертирующем ОУ может быть такой, Рис. 9.50.

Рис. 9.50Активный фильтр ВЧ первого порядка

И его характеристика передачи будет иметь вид:

(9.26)

Сравнивая выражение (9.25) и (9.26) приходим к заключению: К_∞=R₂/R₁ ; ω_с= 1/ =C₁R₁ ;b₂=C₁R₁;b₁ = 1; а₁=C₁R₂. Элементы можно определить следующим образом С₁ ≈ 10/f_c[мкФ],R₁=b₂/C₁,R₂=a₁/C₁или задавшись значениемK_∞.

Другая схема ФВЧ на неинвертирующем ОУ приведена на рис. 9.51.

Рис. 9.51ФВЧ первого порядка

Записав напряжение для узла 3 по аналогии с вышеизложенным получим:

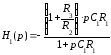
Сравнивая с выражением (9.25) приходим к следующим расчетным формулам для определения элементов схемы: С₁ ≈10/f_c[мкФ];R₁= а₁/C₁=b₂/C₁;;;. При К_∞= 1,R₂→ ∞,R₃= 0.

9.10 Реализация звеньев второго порядка

В общем виде выражение передаточной функции ФНЧ второго порядка для фильтров полиноминального типа можно записать так:

(9.27)

При а₀= 0. А для дробного типа, т.е. при наличие нулей в полосе не пропускания (например: инверсные Чебышева):

(9.28)

На рисунке 9.52 представлена схема ARC- фильтра нижних частот второго порядка с отрицательной обратной связью.

Рис. 9.52Активный фильтр нижних частот второго порядка с отрицательной обратной связью

Для узловых напряжений U₃иU₄на основании законов Киргхофа можно записать:

(9.29)

Учтем, что U₄ = -U₂/μи тогда получим:

(9.30)

Для решения этой системы можно использовать MathCAD. На рисунке 9.53 приведен листинг программы решения системы уравнений с помощью встроенной функцииFind(x,y…)

Рис. 9.53Листинг программы

В блоке Given(Заданно) записывается система уравнений (например, (9.30)), далее указываются, если необходимо, коэффициенты системы и вызывается функцияFind(--) решения системы уравнений с указанием неизвестных в качестве аргумента. В данном примере подU₂подразумевается коэффициент передачиH₂(p) =U₂/U₁. Для решения системы уравнений в символическом виде необходимо на панели инструментов инициализировать значоксимволические операторыи затемсимволический знакравенства( → ).

С учетом того, что μ→ ∞ получим:

Приравняв коэффициенты этой функции с коэффициентами выражения (9.27), получим: a₀= 0,a₂=1,K₀= -R₃/R₁,b₂= 1,b₀ =C₁C₂R₂R₃,b₁ =C₁(R₂+R₃+(R₂R₃/R₁).

Как видно, расчетные формулы справедливы для произвольных положительных значений коэффициентов a_iиb_i. Таким образом, задавая эти значения для конкретных типов фильтров (Баттерворта, Чебышева, Гаусса), можно реализовать эти фильтры по одной схеме. Коэффициент передачи постоянного сигналаK₀фильтра оказывается отрицательным, поэтому прошедший через фильтр низкочастотный сигнал будет инвертирован. Для расчета фильтра можно, например, задать значение сопротивленийR₁иR₃и по приведенным формулам вычислить значениеR₂,C₁иC₂.

Однако чтобы реальная схема фильтра имела желаемую амплитудночастотную характеристику, входящие в неё элементы могут быть подобранны исходя из следующих соображений. При подборе сопротивлений никаких проблем не возникает, поскольку их стандартные номиналы задаются с однопроцентным допуском. Что касается конденсаторов, то допуск их номинальных значений, как правило, составляет 10% и более. В связи с этим лучше при расчете фильтра задавать значение емкостей конденсаторов и вычислять необходимые значения сопротивлений. Поэтому решим уравнение относительно сопротивлений.

С₂ ≈ 10/f_c[мкФ]; С₁≤ С₂;;

; .

Для того, чтобы получить сопротивление R₃было действительным, должно выполняться условие:

При выполнении этого условия в процессе расчета фильтра не следует выбирать отношение C₂/C₁много большим величины, стоящей справа.

Фильтр нижних частот на ОУ с положительной обратной связью может быть реализован по схеме приведенной на рис. 9.54.

Рис. 9.54Фильтр НЧ с ПОС

Запишем уравнения для напряжений в узлах 3 и 4:

При этом U₃=U₂/K₀, аK₀= 1 +R₄/R₃. С учетом этого система уравнений примет вид:

Воспользовавшись программой, листинг которой приведен на рис. 11.55, получим выражение коэффициента передачи:

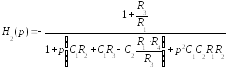
Сравнивая это выражение с уравнением (9.27) находим значение элементов схемы: К₀= 1 +R₄/R₃;;;a₁= 1;, гдевходное сопротивление используемого операционного усилителя.

; ;;;

; ;

Если К_о=1, тоR₃→ ∞, аR₄= 0. Расчеты можно упростить если положитьR₁=R₂=RиC₁=C₂ =C. Тогда;, причем–есть добротность полюсов звеньев фильтра.

Если заменить в схеме на рис. 9.52 сопротивление на емкости и наоборот, то получится ФВЧ второго порядка с отрицательной обратной связью (рис. 9.56).

Рис. 9.56Активный фильтр верхних частот второго порядка с отрицательной обратной связью

Чтобы записать выражение передаточной функции для фильтра верхних частот второго порядка, нужно по формуле (9.27) в соответствии с преобразованием частот вместо pподставить 1/p. Тогда:

(9.31)

При этом полиномиальные коэффициенты знаменателя связаны с подобными коэффициентами ФПНЧ следующим образом:

b_2в=b₀ ;b_1в =b₁ ;b_0в =b₂

По аналогии с ФНЧ второго порядка можно получить передаточную функцию для этого фильтра:

(9.30)

Сравнивая выражения (9.29) и (9.30) находим коэффициент передаточной функции для ФВЧ:

К_∞= – С₁/ С₂;a₁= 1;b_2в= 1;;

Положим , тогда С₂ = С₁/ К_∞и приняв, например,R₂= 1 Ком, легко найти оставшиеся элементы схемы.

Активный фильтр верхних частот на ОУ с положительной ОС показана на рис. 9.57.

Рис. 9.56Активный фильтр верхних частот второго порядка с положительной обратной связью

Его передаточная функция имеет вид:

Элементы схемы можно найти следующим образом:

К₀ ≥ 1; К₀ = 1 +R₄/R₅;R₅≤ 0,01R_оу;;b_2в=;

b_2в=;;;

(или R₂=R₁/ К₀). Для упрощения расчетов можно положитьC₁=C₂ =C.

Из вышеизложенного видно, что коэффициент усиления фильтра не зависит от частоты среза. Существенным недостатком фильтров с положительной ОС является необходимость тщательной подборки коэффициента усиления, так как усилитель может переходить в режим возбуждения. Зато для построения фильтров различного типа достаточно изменить лишь значение коэффициента усиления при одних и тех же значениях элементов схемы.

Для увеличения избирательности фильтров применяют фильтры более высокого порядка. Для этого используют, как указывалось выше, цепочечное соединение звеньев первого и второго порядков. Еще одним путем увеличения избирательности является переход на фильтры дробного типа (например, инверсный Чебышева). Т.е. построение фильтров с нулями передачи в полосе запирания. Для таких фильтров общий вид передаточной характеристики приведен в формуле (9.28).

При реализации такой характеристики ARC-фильтров используют ОУ, в цепи ОС которых включают двойные Т-образные мосты (рис. 9.58).

Рис. 9.57Активный фильтр с двоичным Т–образным мостом

Запишем напряжения для узлов 3, 4, 5:

Воспользовавшись программой MathCAD, решаем систему в символьном виде. Решение будет выглядеть существенно громоздким. Поэтому для упрощения выражения примем:

; ;;;

Результат представлен листингом программы, показанном на рис. 9.59.

Таким образом, функция передачи для звена ARC-фильтра, изображенного на рис. 19.58, примет вид:

Сравнивая это выражение с формулой (9.28) получим:

К₀=1; а₂=1;b₂=1;b₁ =RC;a₀= (RC)²

Значения элементов можно определить следующим образом:

; ;

Можно емкости оставить теми же, а сопротивления взять разными:

R₁=R;R₂=α·R;,

тогда функция передачи примет вид:

Для увеличения добротности фильтра ОУ можно включить в режиме с конечным усилением К₀ (рис. 9.60).

Рис. 9.58ARC-фильтр с двойным Т-образным мостом и коэффициентом усиления К₀> 1

Его функция передачи будет описываться следующим выражением:

Более сложный вариант ARC-фильтра на двойном Т-образном мосте приведен на рис. 9.61.

Рис. 9.59ARC-фильтр на двойном Т-образном мосте

Для упрощения конечного выражения функции передачи будем полагать:

; ;;;R₄ =β·R;

C₄=β·C;

Тогда выражение для функции передачи примет вид:

На рис. 9.62 приведен листинг программы для получения этой передаточной функции.

Примерные значения элементов схемы могут быть найдены следующим образом:

; β = (0,5 ÷ 10); ;

Далее приводится модуль программы расчета НЧ ARC-фильтра. Программа может быть использована для расчета трех типов фильтров: Баттерворта, Чебышева и инверсного Чебышева. Следует учесть, что данной программой можно пользоваться только при добротности звеньев фильтра не более 10. При большей добротности лучше строить звенья по более сложным схемам с использованием двух ОУ в каждом звене.

Подводя итог вышеизложенному, порядок расчета ARC-фильтров может быть таким:

1. По переходным данным выбираем тип аппроксимирующей функции Чебышева, Баттерворта, инверсный Чебышев и т.п.

2. Производится нормирование частот и определяется необходимый порядок ФПНЧ:

–для фильтров Баттерворта;

–для фильтров Чебышева,

где

3. Вычисляются координаты нулей и полюсов передаточной характеристики ФПНЧ. Затем по таблице 9.7 эти координаты пересчитываются для проектируемого типа фильтра.

4. В соответствии с полученными координатами полюсов конструируется теоретическая функция передачи фильтра, которая представляется в виде произведения функций не выше второго порядка.

5. Выбирается схема реализации звеньев фильтра и рассчитываются элементы схемы.

6. Затем выбираются номиналы элементов схемы и осуществляется АЧХ фильтра.

Текст программного модуля расчета нч arc-фильтра

Рис. 9.60 Полюса и нули

Рис. 9.61 Коэффициент передачи фильтра

Рис. 9.62Затухание фильтра

Рис 9.63 Модуль коэффициента передачи фильтра