6.10.6 Пример записи целевой функции при синтезе фильтров

Проектирование фильтра осуществляется путем процедуры синтеза, включающего два этапа – аппроксимацию и реализацию, исходя из заданных полос пропускания и заграждения, и потерь в них. На первом этапе – аппроксимации – производится замена требуемой характеристики затухания фильтра функцией Чебышева или Баттерворта, либо иной зависимостью отвечающей условиям физической реализуемости. На втором этапе – реализация – определяется структура и параметры элементов фильтра.

Применение компьютера позволило изменить данный подход к синтезу фильтров, имеющих ряд ограничений, и повысить точность расчетов за счет возможности учета ряда факторов.

При компьютерном подходе аппроксимация и реализация заменяются процедурой оптимизации. Производится непосредственный расчет характеристик фильтра на основе определенных рекуррентных соотношений. Осуществляется перебор нескольких типовых структур фильтров и оптимизации параметров в каждом варианте на основе поисковых методов глобального и локального минимума целевой функции.

При таком подходе процедура синтеза представляется как множество вариантов анализа с поиском наилучшего из них согласно определенному критерию. Такая методика предусматривает огромный объем рутинных вычислений, поэтому практическая реализация возможна только с применением компьютера.

При составлении программы параметрического синтеза фильтра функция цели, подлежащая минимизации, может быть представлена в следующем виде:

f_n1..f_n2 – полоса пропускания;

f_m1..f_m2 – полоса заграждения;

f_S1..f_S2 – полоса частот фазовой характеристики;

B_п(f_k) – полученное затухание фильтра в полосе пропускания на частоте f_k ;

B_п.тр(f_k) – требуемое затухание фильтра в полосе пропускания;

B_з(f_k) – полученное затухание фильтра в полосе заграждения на частоте f_k ;

B_з.тр(f_k) – требуемое затухание фильтра в полосе заграждения;

φ (f_k) – полученное значение ФЧХ на частоте f = f_k;

φ_тр (f_k) – требуемое значение ФЧХ на той же частоте f = f_k;

V₁, V₂, V₃ – коэффициенты веса, определяющие соотношение требований по затуханию, предъявляющих к полосам пропускания и заграждения, а также другим параметрам.

В качестве примера можно привести задачу минимизации порядка фильтра, обеспечивающего требуемые значения затухания в полосах пропускания и заграждения, а также группового времени запаздывания в полосе пропускания для ФНЧ Баттерворта.

Введем обозначения:

A_min – требуемое затухание фильтра в полосе заграждения;

A_max – требуемое затухание (допустимая неравномерность) фильтра в полосе пропускания;

Ω – текучая частота;

Ω_z – нормированная частота среза (отношение граничной частоты полосы заграждения к граничной частоте полосы пропускания);

Н_Аb(Ω) – амплитудно-частотная характеристика ФНЧ;

L_Аb(Ω) – рабочие затухание ФНЧ;

β_b (Ω) – фазо-частотная характеристика ФНЧ;

τ_b(Ω) – групповое время запаздывания;

Пусть заданы значения:

A_max : ≤ 2; A_min : ≥ 20 ; Ω_z : = 1.6;

Задаем пределы изменения и шаг изменения текущей частоты:

Ω : = 0.2 * Ωz/100 … 2 * Ωz

Wzcp – нормированная частота среза (fгрпн/fв)

Nb – порядок аналогового ФНЧ Баттерворта

Nc – порядок цифрового ФНЧ Чбышева

w – текущая частота

Hb(w) – АЧХ ФНЧ Баттерворта

Нс(w ) – ФЧХ ФНЧ Чебышева

τb(w) – групповое время запаздывания ФНЧ Баттерворта

τс(w) – групповое время запаздывания ФНЧ Чебышева

Amin1 – требуемое рабочее ослабление на частоте среза для фильтра Баттерворта

Amin2 – требуемое рабочее ослабление на частоте среза для фильтра Чебышева

Amax1 и Amax2 – допустимые неравномерности в полосе пропускания фильтров Баттерворта и Чебышева

Задание начальных данных

Допустимые значения группового времени запаздывания (ГВЗ) ФНЧ для аудиосогналов (из норм для трактов звукового вещания)

Fb – верхняя частота в спектре звукового сигнала

Amin – рабочее затухание на частоте среза (граничная частота полосы заграждения)

Amax – неравномерность в полосе пропускания

Допустимая неравномерность группового времени запаздывания τd(w)

Fb:=10000

w1	40/ Fb = 4×10-3	τd(w1)	55 мс
w2	75/ Fb = 7,5×10-3	τd(w2)	24 мс
w3	100/ Fb = 0,01	τd(w3)	20 мс
w4	6400/ Fb = 0,64	τd(w4)	5 мс
w5	7000/ Fb = 0,7	τd(w5)	10 мс
w6	14000/ Fb = 1,4	τd(w6)	8 мс
w7	15000/ Fb = 1,5	τd(w7)	12 мс

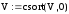
Рис. 6.53 Нормы на ГВЗ

Запишем выражения, необходимые для определения τb(w). Сначала определяется минимально необходимый порядок фильтра, удовлетворяющий заданным параметрам.

То есть требуется ФНЧ Баттерворта 6-го порядка. Далее следует определить наибольший порядок фильтра, удовлетворяющий требованиям по групповой задержке.

Запишем функцию цели для нахождения максимального порядка ФНЧ, удовлетворяющего требованиям по τ. Нормированные частоты выбраны 0,64 (по минимально допустимому значению групповой задержки) и 1 (соответствет Fb). Будем искать минимум функции цели, при котором задержка не превышает допустимого значения.

Введем пределы варьируемых параметров с помощью ключевого слова Given:

Поскольку N – целое число и N может быть меньше 6 для удовлетворения требований по затуханию чем меньше N, тем меньше получается значение τb , то принимаем N=6 и производим проверку на требуемых частотах:

Таким образом, допустимо использование ФНЧ Баттерворта порядка 7, а требуется Nb=6. Следовательно, для Фнч Баттерворта следует принять порядок фильтра равным 6.

Определим теперь требуемый порядок ФНЧ Чебышева:

То есть требуется ФНЧ Чебышева 4-го порядка. Для него произведем проверку получаемого времени задержки на нормированных частотах 0.64 и 1.

Задание начальных значений параметров

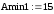
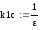
Рис 6.54 Групповое время запаздывания (в мс )

Таким образом ФНЧ Чебышева 4-го порядка удовлетворяет всем предъявляемым требованиям.

Рис. 6.55 АЧХ ФНЧ Чебышева 4-го порядка

Рис 6.56 Зависимости допустимой и полученных групповых задержек

Вопросы для самоконтроля

1. Понятие оптимизациив расчетах РЭА

2. Понятие функции цели

3. Меры расхождения при определении функции цели

4. Методы поиска экстремума функции цели

5. Пример записи функции цели при синтезе фильтров