6.6 Анализ линейных устройств
Определяющим свойством линейных устройств является независимость их параметров, характеристик и свойств от амплитуды сигнала.
Иногда нелинейные устройства могут рассматриваться как линейные при относительно малой амплитуде входного сигнала (не выходит за пределы линейных характеристик).
Математической основой анализа линейных устройств является система линейных дифференциальных уравнений.
Поиск решений базируется на преобразовании Лапласа (временный подход), или Фурье (спектральный анализ).
6.6.1 Передаточная функция, коэффициент передачи, временные и частотные характеристики
Работу линейного устройства определяют два вида характеристик – временные и частотные.
Передаточная функция устройства K(p), позволяющая найти временные характеристики определяется согласно преобразованию Лапласа.
Согласно преобразованию Фурье определяется коэффициент передачи K(jω), определяющий частотные свойства объекта.
Между K(p) и K(jω) существует прямая связь, позволяющая от временных характеристик перейти к частотным и обратно.
Элементарным звеном линейной системы является четырехполюсник (рис. 6.31).
Рис.6.31 Четырехполюсник
Свойства линейного четырехполюсника можно описать с помощью линейного дифференциального уравнения n-й степени:
где X(t) – входной сигнал, а Y(t) – выходной.
Согласно преобразованию Лапласа-Карсона:
где φ(p) – изображение оригинала ψ(t) (значение ψ(t)=0 при t<0).
Уравнение (1) можно записать в операционной форме:
из которой получим передаточную функцию устройства:
или при разложении числителя и знаменателя на множители (n≤m):
где
pa1,
pa2,
pan
– корни уравнения
,
называемые нулями передаточной функцииK(p);
pb1,
pb2,
pbm
- корни уравнения
,
называемые полюсами передаточной
функцииK(p).
В устойчивой системе все полюсы оператора K(p) располагаются в левой полуплоскости комплексного переменного:
т.е. действительные части всех полюсов
Re(pbk)<0, где k=0,1,2….m
6.6.2 Коэффициент передачиK(jω)
,
где
и
– спектральные плотности выходного и
входного сигнала (определяются как
преобразование Фурье отY(t)
и X(t)).
Учитывая, что интеграл Фурье есть частный случай преобразования Лапласа при p=jω из передаточной функции путем подстановки получим комплексный коэффициент передачи устройства:
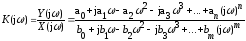
Это выражение можно представить в виде:
,
где модуль и фазу коэффициента передачи можно выразить через действительную и мнимую части комплексного числа:
,
С помощью приведенных выражений можно определить частотные и временные характеристики линейного устройства.
6.6.3 Амплитудно-частотная характеристика (ачх)
Это зависимость модуля комплексного коэффициента передачи от частоты:
Определение АЧХ с помощью пакета программ MathCAD для электрической цепи 2-ого порядка (рис. 6.32).
Рис.6.32 Электрическая цепь 2-ого порядка
Для коэффициента передачи цепи запишем следующее выражение:
,
где
,
,
,
,
.
Примем в программе следующие обозначения:
fp – резонансная частота (Гц);
tk – время (сек);
Q – добротность цепи;
K(f) – комплексный коэффициент передачи K(jω);
A(f) – модуль комплексного коэффициента передачи (в градусах) (ФЧХ);
D(f) – действительная часть комплексного коэффициента передачи;
M(f) – мнимая часть комплексного коэффициента передачи;
NT – число точек отсчета по оси времени;
TH – шаг этого отсчета;
Vb – верхний предел интегрирования по частоте;
Vn – нижний предел интегрирования по частоте;
Фk– переходная характеристика Ф(t);
Нk– импульсная характеристика H(t);
Нижний предел интегрирования не берут равным 0, а принимают равным какому-либо малому значению, например, 0,0001, чтобы избежать деления на 0 при определении переходной характеристики.
Программа расчета частотных характеристик цепи
fp:=10 Q:=5
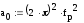
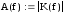
Далее определяются АЧХ и ФЧХ и строятся их графики
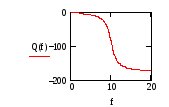
Рис.6.33 График АЧХ Рис.6.34 График ФЧХ