6.4.5 Правила просмотра участков двумерных графиков

Некоторые графики представляют собой довольно сложные кривые. Для детального просмотра любого участка графика следует выделить график, поместить в него указатель мыши и щелкнуть правой клавишей. В появившемся контекстном меню следует выбрать команду Zoom(масштаб). Это ведет к открытию диалогового окнаX-YZoom, с помощью которого можно увеличить любой участок графика. Для того, чтобы воспользоваться этим окном, необходимо предварительно выделить фрагмент графика функции (рис. 6.30).

Рис.6.30 Просмотр участков

При этом в окне просмотра отображаются минимальные и максимальные значения XиY, определяющие область просмотра.

Кнопки Zoom,Unzoom,FullViewпозволяют увеличить выделенную часть графика, снять выделение и вернуться к просмотру всего графика.

Вопросы для самоконтроля

1. Правила построения графиков в декартовой системе координат

2. Правила построения графиков в полярной системе координат

3. Изменение формата графиков

4. Правила трассировки графиков

5. Правила просмотра участков двумерных графиков

6.5 Правила вычислений в среде «MathCad»

Возможны два типа вычислений в среде MathCAD, осуществляемые с помощью формульного редактора:

• численный;

• символьный.

При первом типе результат получается в виде числа, при втором – в форме математического выражения.

Реализация численногоспособа осуществляется:

1. путем обращения к панелям математических инструментов из меню «Вид» (View);

2. путем обращения к встроенным функциям f(x) из меню «Вставка» (Insert);

3. с помощью клавиатуры.

Реализация символьного способа, при котором происходит преобразование одного математического выражения в другое, осуществляется:

1. путем обращения к меню «Символы» (Symbolics);

2. путем обращения к панели математических инструментов «Символы» из меню «Вид»;

3. с помощью клавиатуры.

Запись математических выражений в составляемую программу осуществляется с помощью:

1. математических инструментальных панелей;

2. путем обращения к встроенным функциям f(x);

3. с помощью клавиатуры.

В том месте рабочей области текстового окна, где установлен курсор – стрелка, после щелчка левой клавиши «Мыши» возникает визир в форме значка + красного цвета.

На месте установки визира отражается результат той или иной команды или операции и происходит ввод в программу требуемого математического выражения.

После ввода первого символа визир преобразуется в две линии – горизонтальную и вертикальную – синего цвета.

Перемещение визира осуществляется с помощью мыши при нажатой клавише или клавиш клавиатуры, ответственных за перемещение курсора.

Правила численного и символьного методов решения математических задач в среде «MathCAD»

Правило 1– связано с обращением к панелям математических инструментов из меню «Вид»: «Арифметика», «Матрицы» и «Математический анализ» или «Исчисления».

Оно позволит получить результат в виде числа.

Сначала щелчком вызывается соответствующая панель инструментов, а затем производится щелчок по требуемой пиктограмме (кнопке), после чего в рабочей области текстового окна в месте установки красного визира появляется определенное выражение. Вписывание в него исходных данных и ввод знака равенства дает числовой результат.

Примеры

1. Вычислить косинус угла, равного 0,5 радиана.

Вызываем панель «Арифметика», щелчок по кнопке «cos». В рабочей области текстового окна появляется выражение:

cos ( )

Вписывается внутрь скобок число 0,5 – получаем:

cos (0.5)

Вводим знак ( = ), после чего автоматически получаем результат:

cos (0.5) = 0.878

В меню математика должен стоять автоматический расчет (либо щелкнуть «вычисление») (автоматическое вычисление).

2. Вычислить определенный интеграл от функции sin²(x) в пределах изменения аргумента от 0,5 до 2.

Вызываем панель «Матанализ» («Исчисления»), щелчок по пиктограмме, на которой изображен определенный интеграл.

В рабочей области текстового окна в месте установки красного визира появляется выражение:

Вписываем в него значения верхнего и нижнего пределов интегрирования, а под знаком интеграла заданную функцию, вводим знак =, после чего автоматически получаем результат:

3. Получить из заданной матрицы размером 3х3 транспонированную матрицу.

Вызываем панель инструментов «Матрица» (меню «Вид» → подменю математика).

На ней делаем щелчок по пиктограмме, на которой изображена матрица.

В рабочей области текстового окна в месте установки красного визира появляется диалоговое окно, в котором после слов «строки» и «столбцы» вписываем заданные числа: 3 и 3.

После нажатия на кнопку «ОК» или «Вставить» в тексте программы появляется матрица выбранной размерности. Вписываем в ячейки матрицы требуемые числа.

Обрамляем с помощью курсора всю запись пунктирной линиейи щелкаем по пиктограммеM^Т, означающей выполнение операции по транспонированию матрицы.

Вводим знак равенства, после чего автоматически получаем результат:

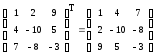
Вызов матрицы можно также произвести путем обращения к подменю «Матрица» из меню «Вставка».

Правило 2– связанное с обращением к встроенным функциямf(x) из меню «Вставка», либо к пиктограмме «Встроенная функцияf(x)» на 2-ой строке текстового окна – стандартной линейке.

Результат будет получен в виде числа.На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбирается определенное имя, тип функции, а в разделе «Название функции» - требуемая функция

После нажатия на кнопку «ОК» или «Вставить» в рабочей области текстового окна появляется выбранная функция, в которую вписываются заданные числа, и вводится знак «=», после чего автоматически получается результат.

Пример

Вычислить функцию Бесселя 1-ого рода 1-ого порядка при аргументе 5.

Обращаемся к пиктограмме встроенная функция f(x) на 2-ой строке текстового окна – стандартной линейке.

На появившемся после щелчка диалоговом окне в разделе «Категория функций» выбираем строку с надписью «Бесселя», а в разделе» Название функций» - I 1.

После нажатия на кнопку «ОК» или «Вставить» в рабочей области текстового окна в месте установки красного визира появляется выражение I 1 ( ■ ).

Вписываем внутрь скобок заданное значение аргумента – I 1 (5) – и вводим знак =, после чего автоматически получаем результат: I 1 (5) = 24.336

Правило 3

Это правило связано с вводом необходимых знаков с помощью клавиатуры. Оно позволяет получить результат, как в численном виде, так и в символьном виде.

Данное правило, по существу, аналогично двум предыдущим.

Только здесь все знаки – числа, арифметические действия и латинские обозначения – вводятся в текст составляемой программы с помощью клавиатуры.

Возможен ввод и специальных операторов при символьных вычислениях путем одновременного нажатия двух или трех клавиш.

Рассмотрим некоторые примеры по вводу специальных знаков:

1. для ввода оператора 1-ой производной следует одновременно нажать на две клавиши: shift+?;

2. для ввода оператора n-ой производной следует одновременно нажать при клавиши: ctrl+shift+?;

3. для ввода знака неопределенного интеграла следует нажать на две клавиши: ctrl+I;

4. для ввода знака определенного интеграла следует нажать две клавиши: shift+&;

5. исполнение символьных операций дифференцирования и интегрирования осуществляется нажатием двух клавиш: shift+F9;

Правило 4

Оно связано с обращением к математической панели инструментов «Символы» (в меню «Вид» →Панели инструментов→Символы) и позволяет получить результат как в символьном, так и численном виде.

1. Математическое выражение, подлежащее преобразованию, записывается в рабочей области текстового окна и с помощью курсора обрамляется рамкой.

2. Далее в зависимости от вида преобразования выбирается соответствующее ключевое слово:

• Ряд – при разложении функции в степенной ряд Маклорена по выбранной переменной;

• Расширить – при разложении в степенной ряд выражений типа бинома Ньютона;

• Комплекс – при преобразовании комплексных чисел;

• Mт→, M-1→, |М|→, - при транспонировании, обращении (инвертировании) матриц и расчете их определителя;

• Символьный знак равенства → - при дифференцировании и т.д.

1. После щелчка по выбранному ключевому слову к записи автоматически добавляется это слово и символический знак равенства →.

2. После второго щелчка вне рамки записи автоматически появляется результат в виде нового символьного выражения, полученного из исходного в результате преобразования.

Примеры

1. 

2. 

3. 

4. 

5. 

6. 

Правило 5

Правило связано с обращением к меню «Символы», подменю «расчеты». Оно позволяет произвести символьные вычисления, в том числе и в комплексной области.

Математические выражения, связанные между собой определенными операциями, записываются в рабочей области текстового окна, и с помощью курсора обрамляются рамкой.

Далее щелчком производится обращение к строке «символические» при дифференцировании функций и других операциях, а при работе с комплексными выражениями – к строке «комплексные».

После щелчка на рабочем столе появляется результат в виде нового выражения, располагаемого под исходной записью.

Примеры

1. 

Используется подменю «Расчеты», опция «символические»

2. 

Используется подменю «Расширить»

3. 

4. 

Используется опция «Символические»

Правило 6

Оно также связано с обращением к меню «Символы».

Позволяет произвести разнообразные символьные преобразования, записав в рабочей области текстового окна подлежащее преобразованию выражение.

При обращении к подменю «Переменные» в этом выражении необходимо выделить (затемнить ■) один символ – переменную – путем протаскивания курсора.

Далее с помощью подменю «Переменные» можно выполнить следующие операции:

• найти корни алгебраического и трансцендентного уравнений (опция «Вычислить»);

• произвести дифференцирование функции (строка «Дифференциалы»);

• произвести интегрирование функции (строка «Интеграция»);

• разложить функцию в степенной ряд Маклорена (строка «Преобразовать в частичные доли»).

При обращении к подменю «Матрица» следует обрамить рамкой все выражение. Это подменю позволяет осуществить транспонирование и обращение (инвертирование) матрицы и найти ее определитель.

При обращении к подменю «Преобразования» можно произвести прямое и обратное преобразования: Фурье, Лапласа и типаZ.

Вопросы для самоконтроля

1. Первое правило решения математических задач в среде MathCAD

2. Второе правило решения математических задач в среде MathCAD

3. Третье правило решения математических задач в среде MathCAD

4. Четвертое правило решения математических задач в среде MathCAD

5. Пятое правило решения математических задач в среде MathCAD

6. Шестое правило решения математических задач в среде MathCAD