10

Министерство Российской Федерации

по связи и информатизации

Сибирский государственный университет

телекоммуникаций и информатики

Кафедра физики

Методические указания

к лабораторной работе по теме

«Исследование биений в связанной системе»

Разработчик: ст. преподаватель Стрельцов А. И.

Новосибирск

2005

Лабораторная работа 5.2.

Исследование биений в связанной системе

Цель работы:

1. Познакомиться со свободными колебаниями механической системы с двумя степенями свободы.

2. Исследовать биения между двумя нормальными модами колебаний двух слабо связанных одинаковых маятников.

Теоретическое введение

Колебаниями называются любые процессы в природе, периодически повторяющиеся во времени.

По своей физической природе колебания могут быть механическими, электромагнитными или электромеханическими. По характеру зависимости амплитуды от времени колебания можно разделить на незатухающие и затухающие. В данной работе нас будут интересовать гармонические колебания в механической колебательной системе.

Процессы, изменение колеблющейся физической величины в которых зависит от времени по закону синуса (или косинуса), называются гармоническими.. Гармонические колебания являются идеализацией, поскольку в реальных колебательных системах всегда существуют силы сопротивления. Поэтому колебания либо затухают, либо требуют для поддержания постоянства амплитуды сообщения энергии извне. Первый случай соответствует свободным затухающим колебаниям, второй – вынужденным колебаниям.

Положение, в котором колебательная система может оставаться в покое неограниченно долго в отсутствие внешних воздействий, называется положением равновесия. Для возбуждения колебаний систему необходимо хотя бы один раз вывести из положения равновесия.

Для гармонических колебаний характерны следующие параметры:

1. Амплитуда – максимальное отклонение колеблющейся величины от положения равновесия. Амплитуда всегда положительна и имеет ту же размерность, что и колеблющаяся величина. Например, амплитуда колебаний напряжения будет измеряться в вольтах.

2. Частота – число полных колебаний за единицу времени. За полное колебание считается два ближайших следующих друг за другом перехода системы через положение равновесия в одном направлении. В системе СИ частота колебаний измеряется в герцах (Гц).

3. Циклическая (круговая) частота – число полных колебаний за 2π единиц времени. Размерность циклической частоты – обратные секунды (с^-1).

4. Период – время одного полного колебания. Измеряется в секундах (с).

5. Фаза – величина, характеризующая значение колеблющейся величины относительно положения равновесия в текущий момент времени. В решении дифференциального уравнения гармонического колебательного процесса фаза – это величина, стоящая под знаком синуса или косинуса. Размерность фазы – радианы.

6. Начальная фаза – значение фазы колебания в момент начала отсчета времени.

Мы будем изучать колебания, происходящие в системе из двух слабо связанных маятников (рисунок 1). Колебания происходят в одной плоскости (в плоскости рисунка). Для полного количественного описания такого колебательного процесса достаточно двух независимых переменных, поэтому говорят о двух степенях свободы рассматриваемой колебательной системы. В качестве таких переменных можно взять любые величины, мы выбрали угловые координаты φ₁ и φ₂.

Рисунок 1. Система связанных маятников.

Рассмотрим случай малых колебаний. Колебания маятников можно считать малыми, если угол их отклонения от положения равновесия стремится к нулю. В этом случае уравнения движения колебательной системы будут линейными, наиболее простыми для решения. При линейных уравнениях движения наиболее общее движение является суперпозицией двух независимых простых гармонических движений, происходящих одновременно. Эти два простых гармонических движения называются нормальными колебаниями или нормальными модами колебаний. В нашей системе возможны два вида колебаний: синфазные и противофазные.

Синфазными называются колебания, разность фаз которых равна нулю (рисунок 2). Такие колебания можно получить в нашей системе двух маятников, отклонив каждый из них в одну и ту же сторону на одинаковый угол и одновременно отпустив.

Противофазными называются колебания, разность фаз которых составляет π радиан (рисунок 3). Их можно получить, отклонив маятники в противоположные стороны на одинаковый угол и также одновременно отпустив.

Рисунок 2. Синфазные колебания. Рисунок 3. Противофазные колебания.

Найдем частоты нормальных колебаний обоих типов.

При синфазных колебаниях длина пружины неизменна, воздействие пружины на маятники будет отсутствовать. Сила, возвращающая маятник к положению равновесия есть составляющая силы тяжести маятника и равна:

(1)

так как угол отклонения маятника от вертикальной оси весьма невелик (случай малых колебаний). Используя определение синуса угла, получим:

(2)

где x – линейное смещение маятника, l – его длина. Из второго закона Ньютона получим дифференциальное уравнение движения маятника:

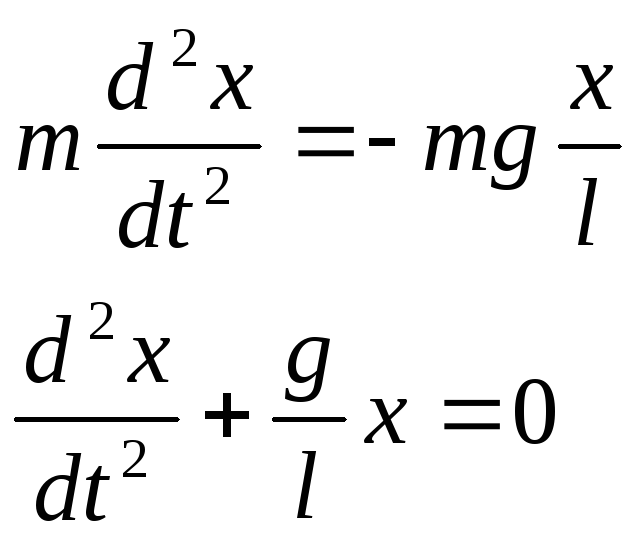(3)

Полученное уравнение является однородным линейным дифференциальным уравнением второго порядка вида

,(4)

где ω₁ – круговая частота синфазных колебаний, l – длина маятника, g – ускорение свободного падения, α – угловое смещение маятника от положения равновесия. В соответствии с принятыми начальными условиями нормальные колебания каждого маятника описываются одним уравнением:

(5)

где α_m- амплитуда углового смещения.

Нормальные противофазные колебания отличаются от синфазных колебаний тем, что в любой момент времени угловые смещения β₁ и β₂ хотя и равны по величине, но противоположны по знаку: β₁= - β₂. Индексы 1 и 2 относятся к первому и второму маятникам. Практически удобно создать такие начальные условия, при которых в момент времени t = 0 маятники имеют наибольшее смещение и скорость, равную нулю, то есть:

Для первого маятника: ,(6)

Для второго маятника: ,(7)

Возвращающая сила, вызванная растянутой или сжатой пружиной, для каждого маятника определяется законом Гука:

(8)

Двойка в законе Гука для упругой деформации здесь появилась потому, что деформация пружины равна

(9)

Возвращающая сила, обусловленная силой тяжести, равна

(10)

Обе эти силы имеют одинаковый знак, поэтому их надо сложить и приравнять к произведению массы маятника на его ускорение. Дифференциальное уравнение с угловым смещением β в качестве переменной имеет вид:

, (11)

где ω₂ – круговая частота нормальных противофазных колебаний, l₁ – расстояние от точки укрепления пружины до точки подвеса маятника, k- жесткость пружины, m – масса маятника.

Приведенные расчеты верны для случая малых колебаний, то есть, малых величин α и β, когда возвращающая сила линейна. Поэтому при выполнении измерений не следует сильно раскачивать маятник, так как при больших углах отклонения выведенные формулы могут оказаться несправедливыми и результат вычислений будет далек от теоретически ожидаемого.

Решения уравнения нормальных противофазных колебаний представляют собой две гармонические функции, характеризующие колебания первого и второго маятников, происходящие в противофазе (разность фаз равна π), что соответствует начальным условиям:

(12)

(13)

Так как , то, то есть, числовые значения β не зависят от времени.

В общем случае движение каждого маятника будет суперпозицией двух нормальных синфазных и противофазных колебаний. Угловые смещения маятников можно определить из соотношений:

для первого маятника (14)

для второго маятника (15)

Биения

Биения – это результат суперпозиции двух гармонических колебаний, имеющих обязательно различные, но близкие по величине частоты.

Эффект биений будет наибольшим, если амплитуды складываемых колебаний одинаковы. Поэтому положим:

,

тогда имеем:

, (16)

. (17)

Перепишем одно из выражений в несколько ином виде. Введем два понятия: «средняя частота» и «частота модуляции»:

, . (18)

А теперь выразим второе выражение через частоты среднюю и модуляции:

, (19)

то есть

, (20)

где

. (21)

Полученное решение является уравнением биений. Это колебание не будет точно гармоническим, так как амплитуда A_мод не постоянна, а лишь почти постоянна, то есть, очень мало изменяется за один цикл колебаний, происходящих с частотой ω_ср.

Рисунок 4. Биения в связанной системе двух маятников.

Понятие периода биений вводится на основе анализа следующих физических процессов. Согласно графикам биений на рисунке 4, построенных в соответствии с уравнением биений, в момент начала отсчета времени вся энергия колебаний системы сосредоточена в первом маятнике. При дальнейшем рассмотрении процесса амплитуда и энергия этого маятника начинают убывать. Энергия колебаний передается от первого маятника ко второму и возвращается обратно. Период биений – это время полного оборота энергии между маятниками. Обратная величина называется частотой биений.

Цикл модуляции в два раза дольше периода биений:

(22)

Заменив значение ω_мод в уравнение, получим выражение для амплитуды биений в виде:

. (23)

И так как , то получим формулу связи значений частот нормальных колебаний с частотой биений:

. (24)

Тогда период биений можно будет вычислить так:

(24’)

где ω₂ –циклическая частота противофазных колебаний, ω₁ –циклическая частота синфазных колебаний.

Схема лабораторной установки

Лабораторная установка представляет собой два маятника, связанных между собой пружиной (рисунок 1). Каждый маятник состоит из стержня, на верхнем конце которого укреплена опорная призма. Груз может быть установлен в любом месте на стержне маятника. Расстояние l₂ отсчитывается от нижней грани опорной призмы маятника до центра масс груза. Концы пружины крепятся на стержнях маятников с помощью муфт с винтами на требуемом расстоянии l₁ от нижней грани призмы.

Для измерения линейного смещения маятника используется масштабная линейка. Время колебательных процессов измеряется электронным секундомером (на рисунке 1 измерительные приборы не показаны). Угловое смещение маятников рассчитывается из геометрических соображений.