
- •5 Основные сведения о программе
- •5.2 Структура интерфейса программы micro-cap 9 и основное меню
- •5.2.1 Интерфейс программы мс9
- •5.2.2 Основные команды меню
- •Component:
- •Options:
- •Analysis:
- •Desing:
- •5.2.3 Создание схемы
- •5.2.4 Представление чисел, переменных и математических выражений
- •Переменные
- •Математические выражения и функции
- •5.2.5. Расчет режима по постоянному току Dynamic dc
- •5.2.6 Расчет передаточных функций по постоянному току dc
- •5.2.7 Расчет переходных процессов transient
- •5.2.8. Анализ частотных характеристик ac
- •5.2.9 Синтез аналоговых фильтров
- •5.2.10 Расчет уровня внутреннего шума
- •5.2.11 Многовариантный анализ
- •5.2.12 Параметрическая оптимизация
- •5.2.13 Функции раздела performance
- •5.2.14 Просмотр и обработка результатов моделирования
- •5.2.15 Трехмерные графики
- •5.2.16 Моделирование цифровых устройств
- •5.2.17 Моделирование функциональных схем
- •5.2.18 Применение программы мс9 для научных исследований
5.2.8. Анализ частотных характеристик ac
В режиме АС сначала рассчитывается режим схемы по постоянному току, затем линеаризуются все нелинейные компоненты и выполняется расчет комплексных амплитуд узловых потенциалов и токов ветвей. При линеаризации цифровые компоненты заменяются их входными и выходными комплексными сопротивлениями, передача сигналов через них не рассматривается.
Ко входу схемы должен быть подключен источник синусоидального или импульсного сигнала PULSE. Этот источник в режиме AC задает место подключения гармонического возмущения с переменной частотой.
При расчете частотных характеристик комплексная амплитуда этого сигнала по умолчанию автоматически полагается равной 1 В, начальная фаза нулевая, а частота меняется в пределах, задаваемых в меню AC Analysis Limits.
Если имеется один источник сигнала, то выходные напряжения будут совпадать с частотными характеристиками устройства. Если же источников сигнала несколько, то отклики от каждого сигнала будут складываться как комплексные величины.
После перехода в режим анализа частотных характеристик программа МС9 проверяет правильность составления схемы. При отсутствии ошибок в схеме программа открывает окно задания параметров моделирования AC Analysis Limits (рисунок 5.22).
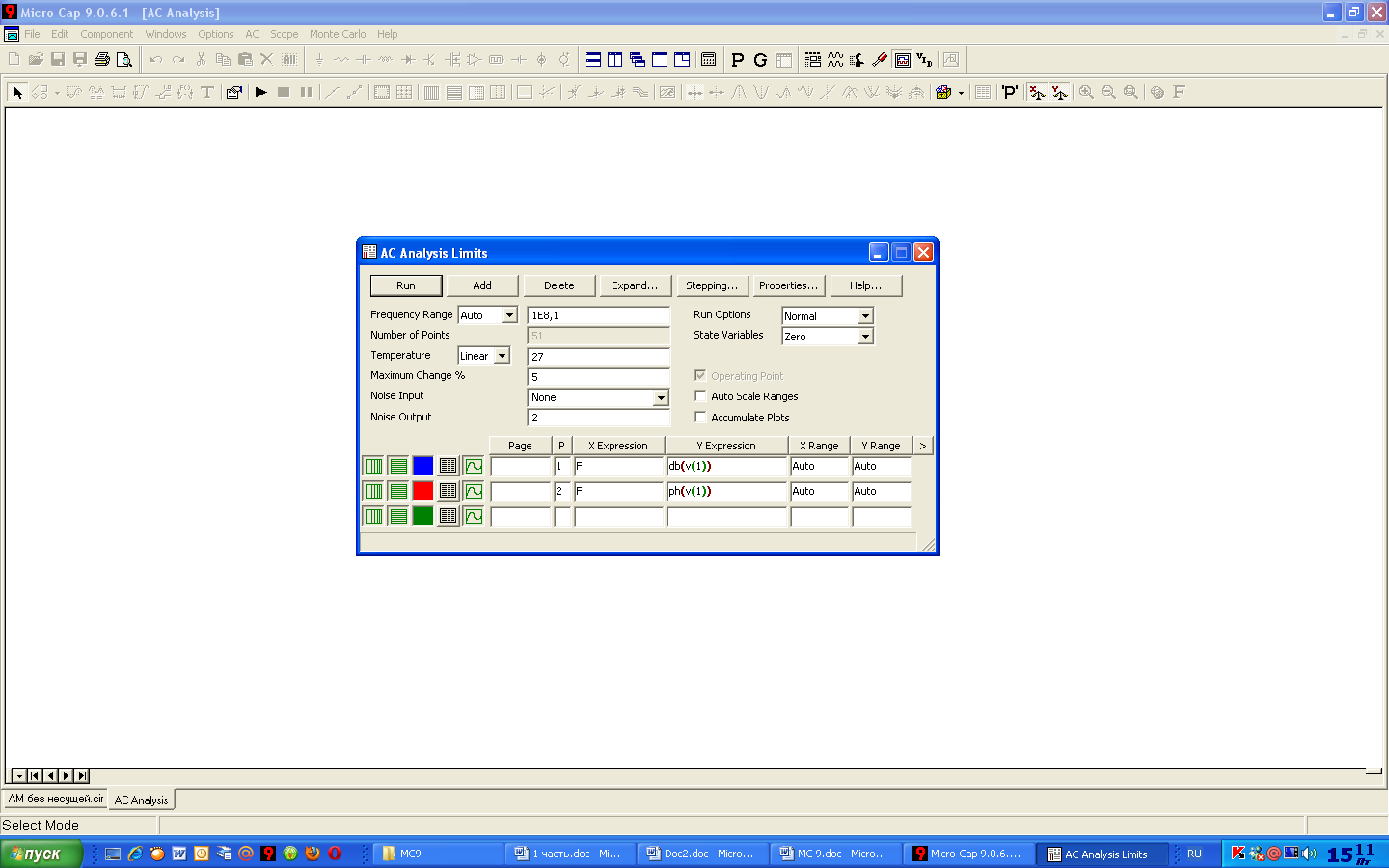
Рисунок 5.22 – Окно задания параметров моделировании в режиме AC.
Как видно из рисунка, набор команд практически не отличается от аналогичных, соответствующих режиму Transient.
Формат задания диапазона частот Frequence Range — fmax[,fmin]. Кроме того, здесь можно выбрать метод вычисления следующей расчетной точки по частоте — Auto, Linear, Log, List.
X Expression — имя переменной, откладываемой по оси X. Обычно при анализе частотных характеристик по этой оси откладывается частота (переменная F), однако это не обязательно. Так при расчете импульсной характеристики с помощью преобразования Фурье по этой оси откладывается время (переменная Т), а при построении годографа для анализа устойчивости по методу Найквиста — действительная составляющая комплексного сигнала.
Y Expression — математическое выражение для переменной, откладываемой по оси Y. Это может быть простая переменная типа напряжения в узле V(5), падение напряжения на двухполюсном компоненте V(L1) или тока ветви I(2,3), I(L1), произведения комплексных величин, например V(VCC)*I(VCC), и другие выражения.
X Range — максимальное и минимальное значение переменной Х на графике по формату High[,Low]. Если минимальное значение Low равно нулю, его можно не указывать. Для автоматического выбора диапазона переменных в этой графе указывается Auto. В этом случае сначала выполняется моделирование, в процессе которого графики строятся в стандартном масштабе и затем автоматически перестраиваются. Удобно также использовать Fmax,Fmin, в этом случае не надо дублировать диапазон, указанный в Frequency Range.
Y Range — максимальное и минимальное значение переменной Y на графике; если минимальное значение равно нулю, его можно не указывать. Для автоматического выбора диапазона переменных в этой графе указывается Auto.
Еще
одной особенностью режима AC
является возможность вывода графиков
как в прамоугольной системе координат
![]() ,
полярной системе координат
,
полярной системе координат![]() ,
а также круговой системе координат
,
а также круговой системе координат![]() т.н. диаграмме Смита.
т.н. диаграмме Смита.
Последовательность вычислений, выполняемая при проведении анализа частотных характеристик, следующая:
1. Рассчитывается режим работы схемы по постоянному току, исходя из величин постоянных источников напряжения и тока в схеме, а также значений постоянных составляющих источников сигнала схемы (атрибут DC для SINE SOURCE и PULSE SOURСE).
2. Составляется линейная эквивалентная схема замещения каждого прибора на переменном токе в окрестности рассчитанного режима по постоянному току.
3. Составляется полная линеаризованная схема замещения анализируемой схемы по переменному току в окрестности рассчитанного режима по постоянному току (ей соответствует система линейных дифференциальных уравнений).
4. Все источники сигнала схемы принимаются синусоидальными с частотой f = fmin и амплитудой А=1 и нулевой начальной фазой .
5. Анализируется схема и находятся отклики в виде комплексных величин узловых потенциалов и токов схемы для линеаризованной схемы на заданной частоте.
6. Для заданной переменной и для заданных величин (Re, Im, Mag, PHASE и пр.) на графиках строятся точки.
7. Увеличивается частота f на заданный шаг и снова производится расчет. Если частота превысила значение fmax, то расчет завершается.
Пример.
Рассчитаем частотные характеристики однокаскадного резонансного усилителя на биполярном транзисторе. На вход усилителя подается сигнал от генератора V1. В качестве источника питания используется батарея V2. Схема и результаты расчетов показаны на рисунке 5.23.
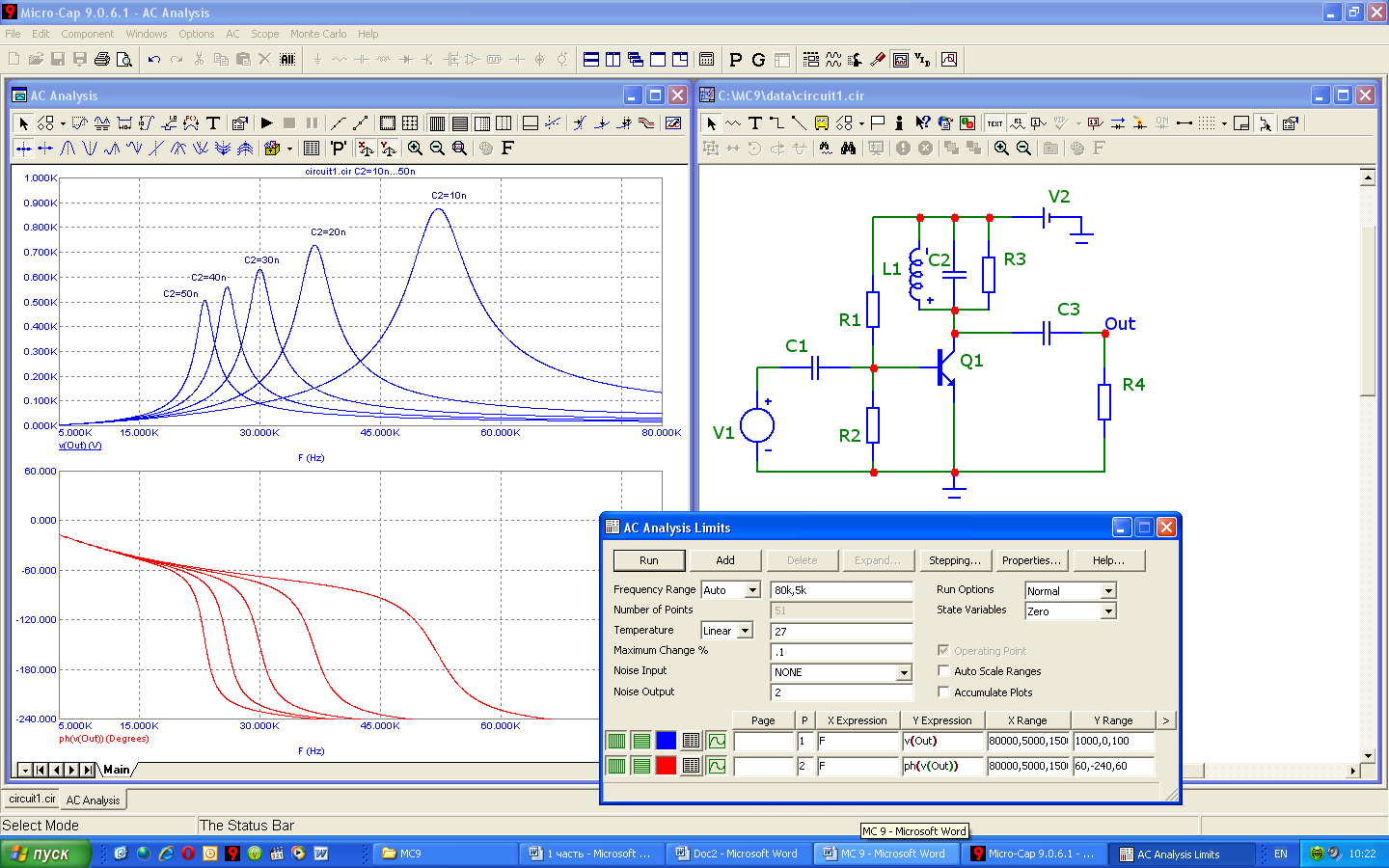
Рисунок 5.23 – АЧХ и ФЧХ резонансного усилителя
Здесь показаны графики проведения многовариантного (пошагового) анализа при изменении номинального значения конденсатора C2. Текстовые надписи соответствующих кривых выполняются по команде Scope > Label Branches .
Пример.
Рассмотрим пример замены некоторого фильтра эквивалентным зависимым источником, задаваемым передаточной функцией.
Пусть задан фильтр в виде следующей принципиальной схемы.
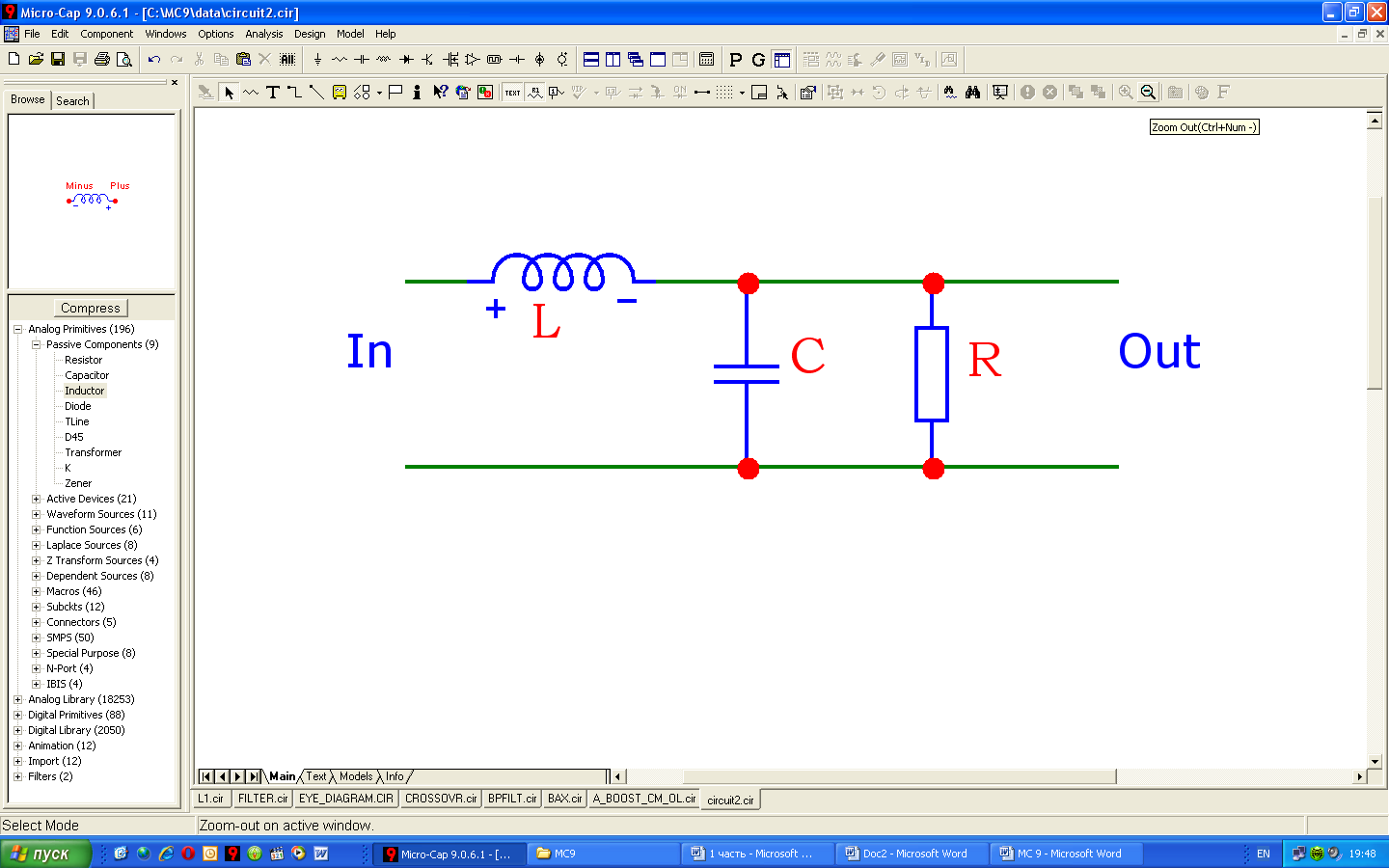
С помощью несложных преобразований можно записать передаточную функцию для заданной схемы в операторной форме:

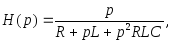
где p — переменная Лапласа.
Теперь создадим в программе МС9 две схемы (рисунок 5.24) — принципиальную схему фильтра, показанную выше, и линейный управляемый источник напряжения заданный передаточной функцией H(p).
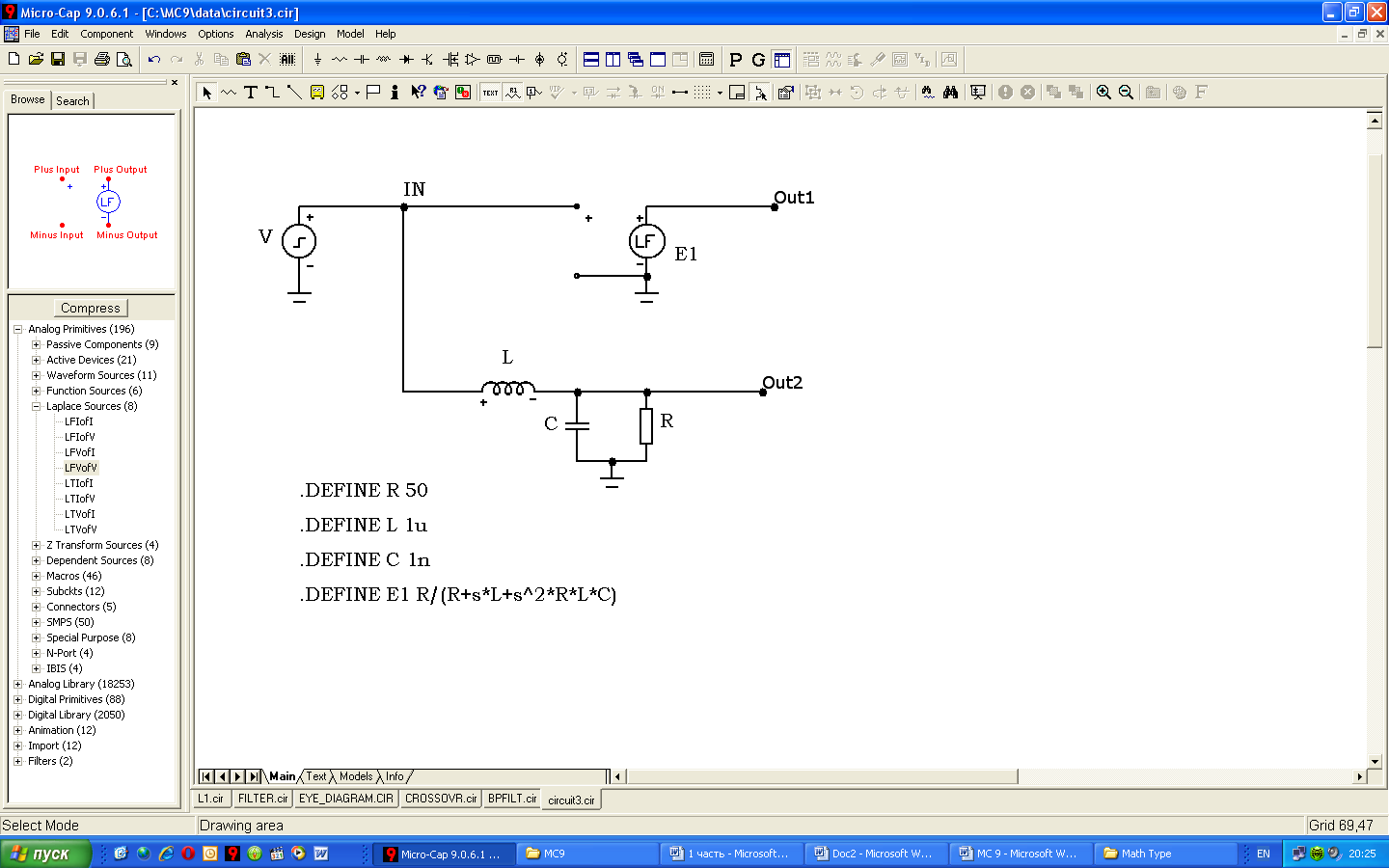
Рисунок 5.24 – Пример замены фильтра управляемым источником
Отметим, что при описании передаточной функции источника напряжения, в качестве переменной Лапласа используется идентификатор s , так как именно он используется для этих целей в европейских странах.
Поведем анализ частотных характеристик представленных устройств — рассчитаем АЧХ для узлов Out1 и Out2. Результаты показаны на рисунке 5.25. Как и следовало ожидать, частотные характеристики совершенно одинаковы. Это дает основания при необходимости заменять принципиальные схемы фильтров их аналогами в виде управляемых источников, что в некоторых случаях существенно облегчает решение задач.
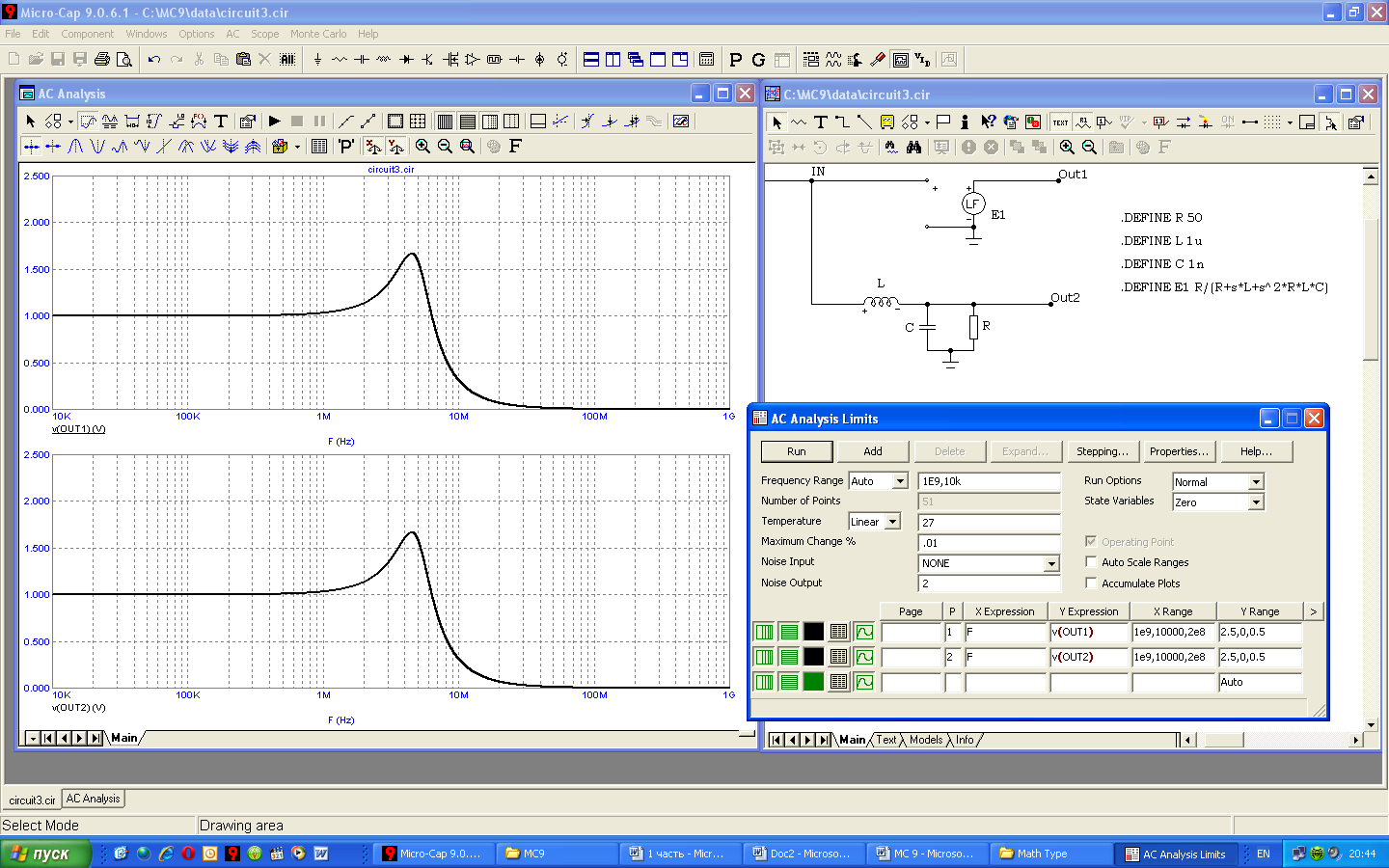
Рисунок 5.25 – Сравнение частотных характеристик
Пример.
Рассмотрим процедуру параметрической оптимизации в режиме анализа частотных характеристик.
Пусть имеется схема, состоящая из трех компонентов – рисунок 5.26. Здесь же приведена АЧХ, рассчитанная для указанных на схеме номинальных значениях компонентов.
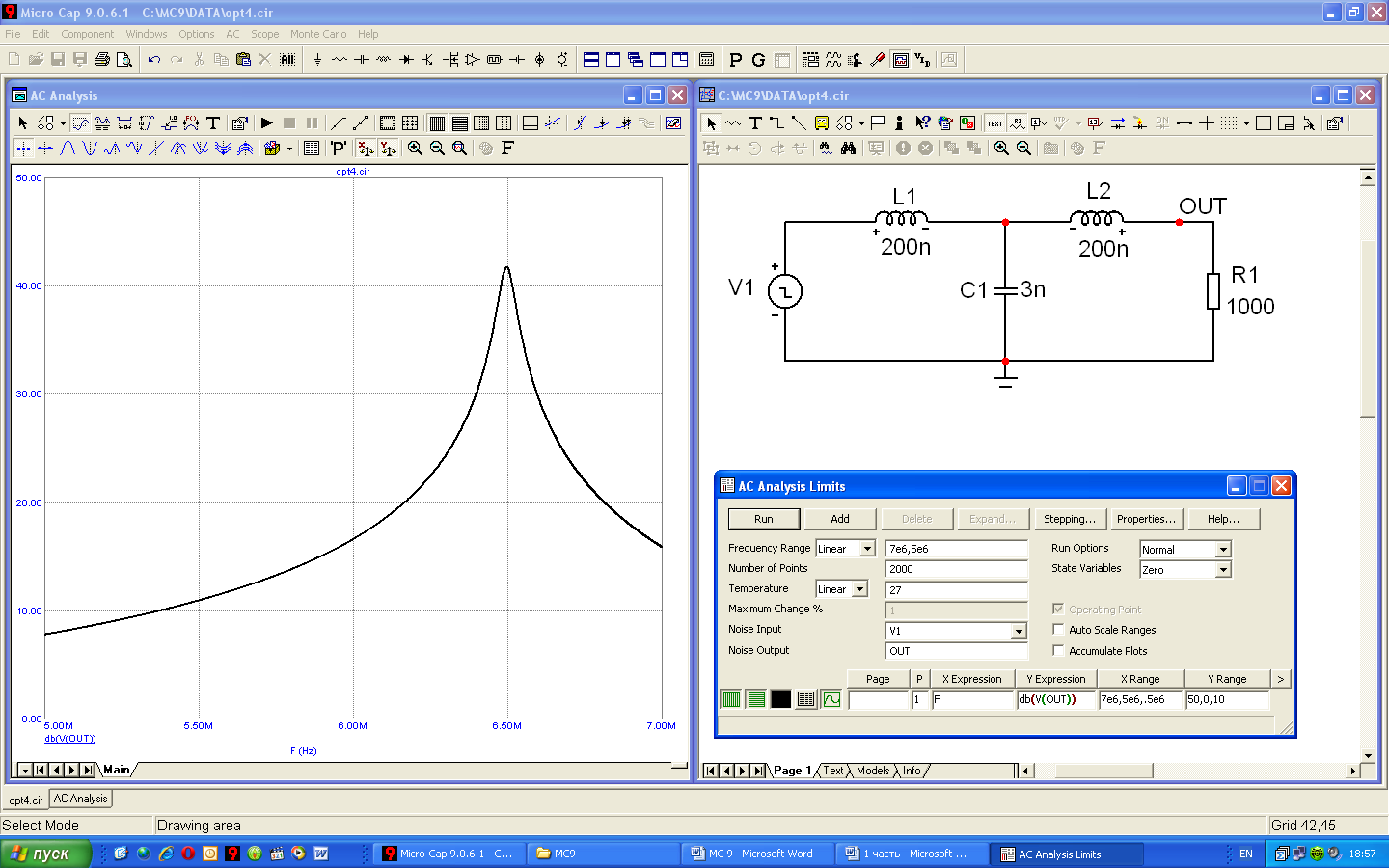
Рисунок 5.26 – Схема и ее АЧХ к примеру 3
Как видно, АЧХ имеет выраженный максимум на частоте 6.5 МГц. Пусть необходимо так подобрать номинальные значения реактивных компонентов, чтобы выполнить три условия:
обеспечить значение коэффициента передачи на частоте 6 МГц не меньшим 50дБ;
обеспечить значение коэффициента передачи на частоте 5.5 МГц не большим 5дБ;
обеспечить значение коэффициента передачи на частоте 6 МГц не большим 3дБ.
Воспользуемся
опцией параметрической оптимизации
Optimize.
Для этого
нажатием иконки
![]() вызываем окно задания параметров
оптимизации (рисунок 5.27), в котором
перечисляем оптимизируемые компоненты
(L1,
L2,
C1),
задаем их минимальные и максимальные
границы, а также записываем условия
определения оптимума — желательные
значения коэффициента передачи на
обозначенных выше частотах. После
проведения оптимизации, присваиваем
компонентам рассчитанные значения и
вновь запускаем расчет АЧХ.
вызываем окно задания параметров
оптимизации (рисунок 5.27), в котором
перечисляем оптимизируемые компоненты
(L1,
L2,
C1),
задаем их минимальные и максимальные
границы, а также записываем условия
определения оптимума — желательные
значения коэффициента передачи на
обозначенных выше частотах. После
проведения оптимизации, присваиваем
компонентам рассчитанные значения и
вновь запускаем расчет АЧХ.
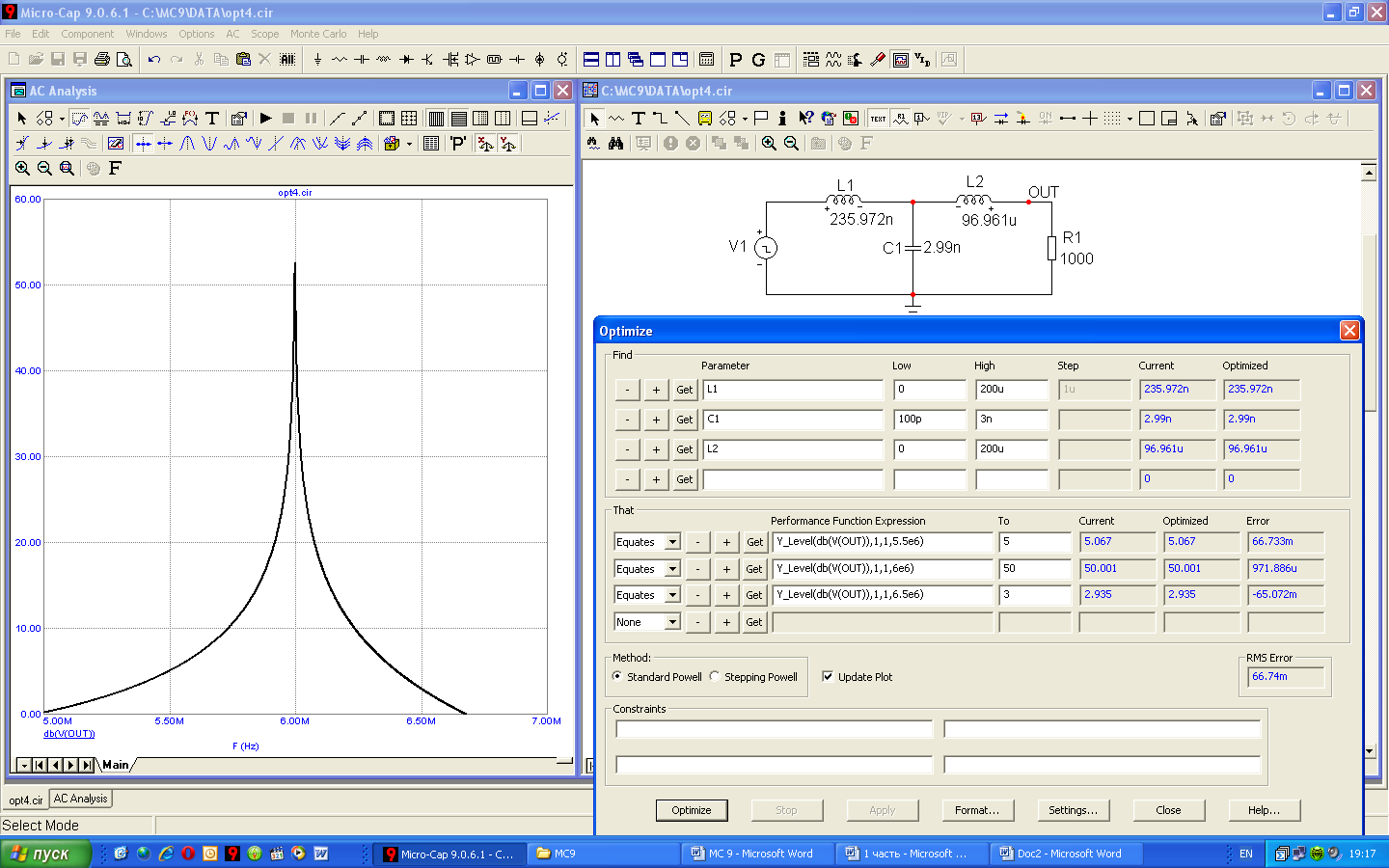
Рисунок 5.27 – АЧХ схемы примера 3 после оптимизации
Как видно из рисунке 5.28 заданные требования к АЧХ выполняются с высокой точностью.
