Формула 2 — определяет модуль вектора dB

 

где альфа это угол между векторами элементарного участка цепи dl и радиус-вектором r.

• Магнитное поле движущегося заряда

Как известно, электрический ток – упорядоченное движение зарядов, а, как мы доказали только что, магнитное поле порождается движущимися зарядами. Найдем магнитное поле, создаваемое одним движущимся зарядом (рис. 1.5).

Рис. 1.5

В уравнении (1.2.2) заменим ток I на jS, где j – плотность тока. Векторы иимеют одинаковое направление, значит

Если все заряды одинаковы и имеют заряд q, то

,

(1.3.1)

где n – число носителей заряда в единице объема; – дрейфовая скорость зарядов.

Если заряды положительные, то иимеют одно направление (рис. 1.4). Подставив (1.3.1) в (1.2.2), получим:

,

(1.3.2)

Обозначим – число носителей заряда в отрезке. Разделив (1.3.2) на это число, получим выражение дляиндукции магнитного поля, создаваемого одним зарядом, движущимся со скоростью :

,

(1.3.3)

В скалярной форме индукция магнитного поля одного заряда в вакууме определяется по формуле:

,

• Вихревой характер магнитного поля

Линии магнитной индукции непрерывны: они не имеют ни начала, ни конца. Это имеет место для любого магнитного поля, вызванного какими угодно контурами с током. Векторные поля, обладающие непрерывными линиями, получили название вихревых полей. Мы видим, что магнитное поле есть вихревое поле. В этом заключается существенное отличие магнитного поля от электростатического

Вихревое электрическое поле.

Другой механизм появления ЭДС индукции связан с тем, что изменение магнитного поля во времени приводит к возникновению электрического поля и ЭДС индукции и объясняется на основе закона сохранения энергии. Принципиальное отличие возникающего электрического поля от поля, создаваемого неподвижными зарядами, в том, что работа по переносу заряженной частицы по замкнутому контуру отлична от нуля, т.е. это поле не потенциальное. Силовые линии этого поля не связаны с зарядами, они замкнуты. Такое поле называется вихревым электрическим полем (в отличие от электростатического поля).

• Магнитный поток

В однородном магнитном поле, модуль вектора индукции которого равен В, помещен плоский замкнутый контур площадью S. Нормаль n к плоскости контура составляет угол a с направлением вектора магнитной индукции В.

Магнитным потоком через поверхность называется величина Ф, определяемая соотношением:

Φ = B · S · cos α

Единица измерения магнитного потока в систем СИ - 1 Вебер (1 Вб).

1 Вб = 1 Тл · 1 м²

Магнитный поток через контур максимален, если плоскость контура перпендикулярна магнитному полю. Значит угол a равен 0⁰ .

Тогда магнитный поток рассчитывается по формуле:

Φ_max = B · S

Магнитный поток через контур равен нулю, если контур располагается параллельно магнитному полю.

Значит угол a равен 90⁰ .

• Циркуляция вектора магнитной индукции

    Возьмем контур l (рис. 2.8), охватывающий прямой ток I, и вычислим для него циркуляцию вектора магнитной индукции , т.е..

Рис. 2.8

      Вначале рассмотрим случай, когда контур лежит в плоскости перпендикулярно потоку (ток I направлен за чертеж). В каждой точке контура вектор направлен по касательной к окружности, проходящей через эту точку (линиипрямого тока – окружности).

      Воспользуемся свойствами скалярного произведения векторов.

       где – проекция dl на вектор ,  но, гдеR – расстояние от прямой тока I до dl.

.

      Отсюда

,

(2.6.1)

      это теорема о циркуляции вектора  :  циркуляция вектора магнитной индукции равна току, охваченному контуром, умноженному на магнитную постоянную.

      Иначе обстоит дело, если ток не охватывается контуром (рис. 2.9).

      При обходе радиальная прямая поворачивается сначала в одном направлении (1–2), а потом в другом (2–1). Поэтому , и следовательно

,

(2.6.2)

Рис. 2.9

      Итак,    ,  гдеI – ток, охваченный контуром L.

      Эта формула справедлива и для тока произвольной формы, и для контура произвольной формы.

      Если контур охватывает несколько токов, то

,

(2.6.3)

т.е. циркуляция вектора равна алгебраической сумме токов, охваченных контуром произвольной формы.

      Теорема о циркуляции вектора индукции магнитного поля позволяет легко рассчитать величинуВ от бесконечного проводника с током (рис. 2.10):    .

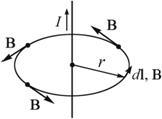
Рис. 2.10

      Итак, циркуляция вектора магнитной индукции отлична от нуля, если контур охватывает ток (сравните с циркуляцией вектора:).

Такие поля, называются вихревыми или соленоидальными.

      Магнитному полю нельзя приписывать потенциал, как электрическому полю. Этот потенциал не был бы однозначным: после каждого обхода по контуру он получал бы приращение .

      Линии напряженности электрического поля начинаются и заканчиваются на зарядах. А магнитных зарядов в природе нет. Опыт показывает, что линии всегда замкнуты (см. рис. 1.2. и 1.7). Поэтому теорема Гаусса для вектора магнитной индукции записывается так:

 

• Действие магнитного поля на движущийся заряд . Сила Лоренца

Сила Лоренца - сила, действующая со стороны магнитного поля на движущуюся электрически заряженную частицу.

где q - заряд частицы; V - скорость заряда;  B - индукции магнитного поля; a - угол между вектором скорости заряда и вектором магнитной индукции.

• Действие магнитного поля на проводники с током. Сила Ампера

Сила Ампера это та сила, с которой магнитное поле действует на проводник, с током помещённый в это поле. Величину этой силы можно определить с помощью закона Ампера. В этом законе определяется бесконечно малая сила для бесконечно малого участка проводника. Что дает возможность применять этот закон для проводников различной формы.

 

Формула 1 — Закон Ампера

 

B индукция магнитного поля, в котором находится проводник с током

I сила тока в проводнике

dl бесконечно малый элемент длинны проводника с током

альфа угол между индукцией внешнего магнитного поля и направлением тока в проводнике

 Направление силы Ампера находится по правилу левой руки.

 Из закона Ампера следует, что сила Ампера будет равна нулю, если угол между линией магнитной индукции поля и током будет равен нулю. То есть проводник будет располагаться вдоль такой линии. И сила Ампера будет иметь максимально возможное значение для этой системы, если угол будут составлять 90 градусов. То есть ток будет перпендикулярен линии магнитной индукции.

 С помощью закона Ампера можно найти силу, действующую в системе из двух проводников. Представим себе два бесконечно длинных проводника, которые находятся на расстоянии друг от друга. По этим проводникам протекают токи. Силу, действующую со стороны поля создаваемого проводником с током номер один на проводник номер два можно представить в виде.

Формула 2 — Сила Ампера для двух параллельных проводников.

• Контур с током в магнитном поле

Рис. 4.13

Пусть в однородное магнитное поле помещена рамка с током (рис. 4.13). Тогда силы Ампера, действующие на боковые стороны рамки, будут создавать вращающий момент, величина которого пропорциональна магнитной индукции, силе тока в рамке, ее площади S и зависит от угла a между вектором и нормалью к площади:

.

Направление нормали выбирают так, чтобы в направлении нормали перемещался правый винт при вращении по направлению тока в рамке.

Максимальное значение вращательный момент имеет тогда, когда рамка устанавливается перпендикулярно магнитным силовым линиям:

.

Это выражение также можно использовать для определения индукции магнитного поля:

.

Величину, равную произведению , называют магнитным моментом контураР_т. Магнитный момент есть вектор, направление которого совпадает с направлением нормали к контуру. Тогда вращательный момент можно записать

.

При угле a = 0 вращательный момент равен нулю. Значение вращательного момента зависит от площади контура, но не зависит от его формы. Поэтому на любой замкнутый контур, по которому течет постоянный ток, действует вращательный момент М, который поворачивает его так, чтобы вектор магнитного момента установился параллельно вектору индукции магнитного поля.

• Магнитный момент контура с током

Опыт показывает, что электрические токи взаимодействуют между собой, напрмер, токи Iпритягиваются, а токи Iотталкиваются. Взаимодействие токов осуществляется через поле, которое называется магнитным. Следовательно, движущиеся заряды (токи ) изменяют свойства окружающего их пространства - создают в нем магнитное поле. Это поле проявляется в том, что на движущиеся в нем заряды (токи) действуют силы. Подобно тому, как для исследования электрического поля мы использовали пробный заряд, применим для исследования магнитного поля пробный ток, циркулирующий в плоском замкнутом контуре очень малых размеров . Будем называть такой контур пробным контуром.

Ориентацию его в пространстве характеризует направление нормали к контуру, восстанавливаемой по правилу правого буравчика: вращаем рукоятку правого буравчика по направлению тока в контуре, тогда направление его поступательного движения даст направление нормали (см. рис. 1). Помещая пробный контур в магнитное поле, обнаружим, что поле стремится повернуть контур (нормаль) в определенном направлении.

Вращающий момент, действующий на контур, зависит как от свойств магнитного поля в данной точке, так и от свойств контура. Оказывается, что максимальная величина вращающего момента пропорциональна IS, т.е. M ~ IS, где I -ток контуре, S - площадь контура с током, (рис. 1). Векторную величину (1)

называют магнитным моментом контура, который в СИ измеряется в А×м².

На пробные контуры с разными р_m, помещаемыми в данную точку магнитного поля, будут действовать разные по величине максимальные вращающие моменты М, но отношение М / рбудет для всех контуров одинаково, оно будет являться силовой характеристикой магнитного поля, которая называется магнитной индукцией

В = М /р. (2)

Магнитная индукция есть вектор, направление которого совпадает с направлением нормали контура с током, свободно установившегося во внешнем магнитном поле(см.рис.2)

Поле вектора В можно представить с помощью силовых линий, (см. рис. 2), как и поле вектора ; таким образом В является аналогом Е.Магнитная индукция в СИ измеряется в теслах: 1 Тл=1 Нм/1 А×м². Тесла равен магнитной индукции однородного поля, в котором на плоский контур с током, который имеет магнитный момент 1 А м², действует максимальный вращающий момент, равный 1 Нм.

На контур с током, помещенный в магнитное поле с индукцией , действует вращающий момент . (3)

Величина его M = 

при имеем М = M= pB , при = 0 или = , M= 0.

• Работа по перемещения проводника с током в постоянном магнитном поле

Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле , перпендикулярном к плоскости контура. При показанном на рисунке направлении токаI, вектор сонаправлен с.

Рис. 2.17

      На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо:

      Пусть проводник l переместится параллельно самому себе на расстояние  dx. При этом совершится работа:

      Итак,

,

(2.9.1)

      Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.

      Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.

      Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.

      Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток , пронизывающий контур, направлен по нормалик контуру, поэтому.

Рис. 2.18

      Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и  новый контур будет пронизан магнитным потоком .

      Площадка 4-3-2'-1'-4, расположенная между старым и новым контуром, пронизывается потоком .

      Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:

где ,  равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).

 .

      Провод 1–2 перерезает поток ( ), но движется против сил действия магнитного поля.

 .

      Тогда общая работа по перемещению контура

  или

,

(2.9.2)

здесь  – это изменение магнитного потока, сцепленного с контуром.

      Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром.

      Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле

,

(2.9.5)

      Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины dФ различен.

      Соотношение (2.9.5), выведенное нами для простейшего случая, остаётся справедливым для контура любой формы в произвольном магнитном поле. Более того, если контур неподвижен, а меняется , то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу

• Взаимодействие двух параллельных проводников с током

 Пусть b – расстояние между двумя параллельными, бесконечно длинными проводниками (рис. 2.2). Задачу следует решать так: один из проводников создаёт магнитное поле, второйнаходится в этом поле.

            Магнитная индукция, создаваемая током на расстоянииb от него:

,

(2.2.1)

      

Рис. 2.2

      Если илежат в одной плоскости, то угол междуипрямой, следовательно.  Тогда сила, действующая на элементтока,

,

(2.2.2)

      На каждую единицу длины проводника действует сила

,

(2.2.3)

(разумеется, со стороны первого проводника на второй действует точно такая же сила).

      Результирующая сила равна одной из этих сил. Если эти два проводника будут воздействовать на третий, тогда их магнитные поля и  нужно сложить векторно.

• Явление электромагнитной индукции

Явление электромагнитной индукции заключается в возникновении электрического тока в замкнутом проводнике при изменении магнитного потока, пронизывающего охваченную проводником площадь.

Закон Фарадея

Согласно закону электромагнитной индукции Фарадея (в СИ):

где

—электродвижущая сила, действующая вдоль произвольно выбранного контура,

—магнитный поток через поверхность, натянутую на этот контур.

Знак «минус» в формуле отражает правило Ленца.

Индукционный ток, возникающий в замкнутом проводящем контуре, имеет такое направление, что создаваемое им магнитное поле противодействует тому изменению магнитного потока, которым был вызван данный ток.

Для катушки, находящейся в переменном магнитном поле, закон Фарадея можно записать следующим образом:

Где — электродвижущая сила,— число витков,— магнитный поток через один виток,— потокосцепление катушки.

• Правило Ленца

Физическая суть правила

Согласно закону электромагнитной индукции Фарадея при изменении магнитного потока , пронизывающего электрический контур, в нём возбуждается ток, называемый индукционным. Величина электродвижущей силы, ответственной за этот ток, определяется уравнением^[1]:

где знак «минус» означает, что ЭДС индукции действует так, что индукционный ток препятствует изменению потока. Этот факт и отражён в правиле Ленца.

Правило Ленца носит обобщённый характер и справедливо в различных физических ситуациях, которые могут отличаться конкретным физическим механизмом возбуждения индукционного тока. Так, если изменение магнитного потока вызвано изменением площади контура (например, за счёт движения одной из сторон прямоугольного контура), то индукционный ток возбуждается силой Лоренца, действующей на электроны перемещаемого проводника в постоянном магнитном поле. Если же изменение магнитного потока связано с изменением величины внешнего магнитного поля, то индукционный ток возбуждается вихревым электрическим полем, появляющимся при изменении магнитного поля. Однако в обоих случаях индукционный ток направлен так, чтобы скомпенсировать изменение потока магнитного поля через контур.

Если внешнее магнитное поле, пронизывающее неподвижный электрический контур, создаётся током, текущим в другом контуре, то индукционный ток может оказаться направлен как в том же направлении, что и внешний, так и в противоположном: это зависит от того, уменьшается или увеличивается внешний ток. Если внешний ток увеличивается, то растёт создаваемое им магнитное поле и его поток, что приводит к появлению индукционного тока, уменьшающего это увеличение. В этом случае индукционный ток направлен в сторону, противоположную основному. В обратном случае, когда внешний ток уменьшается со временем, уменьшение магнитного потока приводит к возбуждению индукционного тока, стремящегося увеличить поток, и этот ток направлен в ту же сторону, что и внешний ток.

• Явление самоиндукции

Самоиндукция — это явление возникновения ЭДС индукции в проводящем контуре при изменении протекающего через контур тока.

При изменении тока в контуре пропорционально меняется^] и магнитный поток через поверхность, ограниченную этим контуром. Изменение этого магнитного потока, в силу закона электромагнитной индукции, приводит к возбуждению в этом контуре индуктивной ЭДС.

Величина ЭДС самоиндукции пропорциональна скорости изменения силы тока :

.

Коэффициент пропорциональности называется коэффициентом самоиндукции или индуктивностью контура (катушки).

Самоиндукция и синусоидальный ток

В случае синусоидальной зависимости тока, текущего через катушку, от времени, ЭДС самоиндукции в катушке отстает от тока по фазе на (то есть на 90°), а амплитуда этой ЭДС пропорциональна амплитуде тока, частоте и индуктивности (). Ведь скорость изменения функции — это её первая производная, а .

• Энергия магнитного поля

Работа электрического поля по перемещению заряда

Понятие работы электрического поля по перемещению заряда вводится в полном соответствии с определением механической работы:

где  — разность потенциалов (также употребляется термин напряжение).

Во многих задачах рассматривается непрерывный перенос заряда в течение некоторого времени между точками с заданной разностью потенциалов , в таком случае формулу для работы следует переписать следующим образом:

где  — сила тока.

Мощность электрического тока в цепи

Мощность электрического тока для участка цепи определяется обычным образом, как производная от работы по времени, то есть выражением:

Это наиболее общее выражение для мощности в электрической цепи.

С учётом закона Ома

электрическую мощность, выделяемую на сопротивлении , можно выразить как через ток

,

так и через напряжение:

Соответственно, работа (выделившаяся теплота) является интегралом мощности по времени:

Энергия электрического и магнитного полей

Для электрического и магнитного полей их энергия пропорциональна квадрату напряжённости поля. Строго говоря, термин «энергия электромагнитного поля» является не вполне корректным. Вычисление полной энергии электрического поля даже одного электрона приводит к значению, равному бесконечности, поскольку соответствующий интеграл (см. ниже) расходится. Бесконечная энергия поля вполне конечного электрона составляет одну из теоретических проблем классической электродинамики. Вместо него в физике обычно используют понятие плотности энергии электромагнитного поля (в определённой точке пространства). Общая энергия поля равняется интегралу плотности энергии по всему пространству.

Плотность энергии электромагнитного поля является суммой плотностей энергий электрического и магнитного полей.

В системе СИ:

В вакууме (а также в веществе при рассмотрении микрополей):

где E — напряжённость электрического поля, B — магнитная индукция, D — электрическая индукция, H — напряжённость магнитного поля, с — скорость света,  — электрическая постоянная и  — магнитная постоянная. Иногда для констант и  — используют термины диэлектрическая проницаемость и магнитная проницаемость вакуума, — которые являются крайне неудачными, и сейчас почти не употребляются.

В системе СГС