
- •Физика экзамен т.1 Основы классической механики Кинематика.
- •Механика
- •Т.2 Основы статистической физики и термодинамики Статистическая физика
- •Взаимосвязь кинетической энергии движения молекул и температур Основы термодинамики
- •Т.3 Электростатика
- •Теорема Гаусса для электрической индукции (электрического смещения)
- •Теорема Гаусса для электрической индукции (электрического смещения)[
- •Теорема Гаусса для магнитной индукции
- •Теорема Гаусса для ньютоновской гравитации
- •Т.4 Постоянный электрический ток
- •Т.5 Электромагнетизм
- •Формула 1 — Закон Био Савара Лапласа
- •Формула 2 — определяет модуль вектора dB
- •Т.6. Основы теории Максвелла
- •Т. 7. Физика колебательных процессов
- •§1.1. Механические гармонические колебания.
- •§1.2. Зависимость амплитуды и начальной фазы колебаний от начальных условий.
- •§1.3. Свободные гармонические колебания в lc-контуре.
- •§1.4. Графическое изображение гармонических колебаний. Векторная диаграмма.
- •Глава 2. Сложение гармонических колебаний
- •§2.1. Сложение гармонических колебаний одного направления.
- •§2.2. Сложение взаимно перпендикулярных колебаний.
- •Глава 3. Затухающие колебания.
- •§3.1. Механические затухающие колебания.
- •§3.2. Электромагнитные затухающие колебания.
- •§3.3. Характеристики затухающих колебаний.
- •Глава 4. Вынужденные колебания.
- •§4.1. Общие признаки вынужденных механических и электромагнитных колебаний.
- •§4.2. Зависимости амплитуды вынужденных колебаний и сдвига фаз от частоты внешнего воздействия. Резонанс.
Теорема Гаусса для электрической индукции (электрического смещения)
Для поля в диэлектрической среде электростатическая теорема Гаусса может быть записана еще и иначе (альтернативным образом) — через поток вектора электрического смещения(электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:
|
СГС |
СИ |
|
|
|
В дифференциальной форме:
|
СГС |
СИ |
|
|
|
Теорема Гаусса для электрической индукции (электрического смещения)[
Для поля в диэлектрической среде электростатическая теорема Гаусса может быть записана еще и иначе (альтернативным образом) — через поток вектора электрического смещения(электрической индукции). При этом формулировка теоремы выглядит следующим образом: поток вектора электрического смещения через замкнутую поверхность пропорционален заключённому внутри этой поверхности свободному электрическому заряду:
|
СГС |
СИ |
|
|
|
В дифференциальной форме:
|
СГС |
СИ |
|
|
|
Теорема Гаусса для магнитной индукции
Поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

или в дифференциальной форме
![]()
Это эквивалентно тому, что в природе не существует «магнитных зарядов» (монополей), которые создавали бы магнитное поле, как электрические заряды создают электрическое поле[5]. Иными словами, теорема Гаусса для магнитной индукции показывает, что магнитное поле является (полностью) вихревым.
Теорема Гаусса для ньютоновской гравитации
Для напряжённости поля ньютоновской гравитации (ускорения свободного падения) теорема Гаусса практически совпадает с таковой в электростатике, за исключением только констант (впрочем, всё равно зависящих от произвольного выбора системы единиц) и, главное, знака[6]:

![]()
где g — напряжённость гравитационного поля, M — гравитационный заряд (то есть масса) внутри поверхности S, ρ — плотность массы, G — ньютоновская константа.
Проводники в электрическом поле. Поле внутри проводника и на его поверхности.
Проводниками называют тела, через которые электрические заряды могут переходить от заряженного тела к незаряженному. Способность проводников пропускать через себя электрические заряды объясняется наличием в них свободных носителей заряда. Проводники - металлические тела в твердом и жидком состоянии, жидкие растворы электролитов. Свободные заряды проводника, внесенного в электрическое поле, под его действием приходят в движение. Перераспределение зарядов вызывает изменение электрического поля. Когда напряженность электрического поля в проводнике становится равной нулю, электроны прекращают движение. Явление разделения разноименных зарядов в проводнике, помещенным в электрическое поле называется электростатической индукцией. Внутри проводника электрического поля нет. Это используют для электростатической защиты - защиты с помощью металлических проводников от электрического поля. Поверхность проводящего тела любой формы в электрическом поле является эквипотенциальной поверхностью.
Конденсаторы
Для получения устройств, которые при небольшом относительно среды потенциале накапливали бы на себе (конденсировали) заметные по величине заряды используют тот факт, что электроемкость проводника возрастает при приближении к нему других тел. Действительно, под действием поля, создаваемого заряженными проводниками, на поднесенном к нему теле возникают индуцированные (на проводнике) или связанные (на диэлектрике) заряды (рис.15.5). Заряды, противоположные по знаку заряду проводника q располагаются ближе к проводнику, чем одноименные с q, и, следовательно, оказывают большое влияние на его потенциал.

Поэтому
при поднесении к заряженному проводнику
какого либо тела напряженность
поля ![]() уменьшается,
а, следовательно, уменьшается потенциал
проводника. Согласно уравнение
уменьшается,
а, следовательно, уменьшается потенциал
проводника. Согласно уравнение ![]() это
означает увеличение емкости проводника.
это
означает увеличение емкости проводника.

Конденсатор состоит из двух проводников (обкладок) (рис.15.6), разделенных прослойкой диэлектрика. При приложении к проводнику некоторой разности потенциалов его обкладки заряжаются равными по величине зарядами противоположного знака. Под электроемкостью конденсатора понимается физическая величина, пропорциональная заряду q и обратно пропорциональна разности потенциалов между обкладками
![]()
Определим емкость плоского конденсатора.
Если площадь обкладки S , а заряд на ней q, то напряженность поля между обкладками
![]()
С
другой стороны разность потенциалов
между обкладками ![]() откуда
откуда![]()
Энергия системы точечных зарядов, заряженного проводника и конденсатора.
Всякая система зарядов обладает некоторой потенциальной энергией взаимодействия, которая равна работе, затраченной на создание этой системы. Энергия системы точечных зарядов q1, q2, q3,… qN определяется следующим образом:
![]() ,
,
где φ1 – потенциал электрического поля, создаваемого всеми зарядами кроме q1 в той точке, где находится зарядq1 и т.д. Если изменяется конфигурация системы зарядов, то изменяется и энергия системы. Для изменения конфигурации системы необходимо совершение работы.
Потенциальную
энергию системы точечных зарядов можно
рассчитать другим способом. Потенциальная
энергия двух точечных зарядов q1, q2
на расстоянии ![]() друг
от друга равна
друг
от друга равна .
Если зарядов несколько, то потенциальную
энергию этой системы зарядов можно
определить как сумму потенциальных
энергий всех пар зарядов, которые можно
составить для этой системы. Так, для
системы трех положительных зарядов
энергия системы равна
.
Если зарядов несколько, то потенциальную
энергию этой системы зарядов можно
определить как сумму потенциальных
энергий всех пар зарядов, которые можно
составить для этой системы. Так, для
системы трех положительных зарядов
энергия системы равна
 .
.
|
Электрическое
поле точечного заряда q0 на
расстоянии
|
Потенциал – скаляр, его знак зависит от знака заряда, создающего поле. |
|
Электрическое
поле равномерно заряженной сферы
радиуса
|
Вне сферы:
Потенциал
внутри сферы постоянен и равен а напряженность внутри сферы равна нулю
|
|
Электрическое поле равномерно заряженной бесконечной плоскости с поверхностной плотностью σ(см. рисунок 3.1.5).
|
Поле, напряженность которого во всех точках одинакова, называется однородным. Поверхностная
плотность σ –
заряд единицы поверхности ( |
|
Электрическое поле плоского конденсатора с одинаковыми по величине, но противоположными по знаку зарядами на пластинах (см. рисунок 3.1.6).
|
Напряженность
между обкладками плоского конденсатора Разность
потенциалов uмежду
пластинами (обкладками) конденсатора: Поверхностная
плотность заряда |
Энергия заряженного уединенного проводника и конденсатора
Если
уединенный проводник имеет заряд q, то
вокруг него существует электрическое
поле, потенциал которого на поверхности
проводника равен ![]() ,
а емкость - С. Увеличим заряд на величину
dq. При переносе заряда dq из бесконечности
должна быть совершена работа равная
,
а емкость - С. Увеличим заряд на величину
dq. При переносе заряда dq из бесконечности
должна быть совершена работа равная ![]() .
Но потенциал электростатического поля
данного проводника в бесконечности
равен нулю
.
Но потенциал электростатического поля
данного проводника в бесконечности
равен нулю ![]() .
Тогда
.
Тогда
![]()
При переносе заряда dq с проводника в бесконечность такую же работу совершают силы электростатического поля. Следовательно, при увеличении заряда проводника на величину dq возрастает потенциальная энергия поля, т.е.
![]()
Проинтегрировав данное выражение, найдем потенциальную энергию электростатического поля заряженного проводника при увеличении его заряда от нуля до q:

Применяя
соотношение ![]() ,
можно получить следующие выражения для
потенциальной энергии W:
,
можно получить следующие выражения для
потенциальной энергии W:
![]()
Для
заряженного конденсатора разность
потенциалов (напряжение) равна ![]() поэтому
соотношение для полной энергии его
электростатического поля имеют вид
поэтому
соотношение для полной энергии его
электростатического поля имеют вид
![]()





 Рисунок
3.1.3
Рисунок
3.1.3 ;
; 
 Рисунок
3.1.4.
Рисунок
3.1.4. ;
; 
 ,
,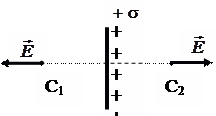 Рисунок
3.1.5.
Рисунок
3.1.5. Рисунок
3.1.6
Рисунок
3.1.6 ,
вне конденсатораЕ=0.
,
вне конденсатораЕ=0.