§3.1. Механические затухающие колебания.

Механическая система: пружинный маятник с учетом сил трения. Силы, действующие на маятник:

1.       Упругая сила. , где  k – коэффициент жесткости пружины, х – смещение маятника от положения равновесия.

2.       Сила сопротивления. Рассмотрим силу сопротивления, пропорциональную скорости v движения (такая зависимость характерна для большого класса сил сопротивления): . Знак «минус» показывает, что направление силы сопротивления противоположно  направлению скорости движения тела. Коэффициент сопротивления r численно равен силе сопротивления, возникающей при единичной скорости движения тела:

 

.

 

Закон движения пружинного маятника – это второй закон Ньютона: ma = F_упр. + F_сопр. Учитывая, что

 

 и , запишем второй закон Ньютона в виде:.

 

 

Разделив все члены уравнения на m, перенеся их все  в правую часть, получим дифференциальное уравнение затухающих колебаний:

 

.

 

Обозначим ,  где β – коэффициент затухания,, где  ω₀ – частота незатухающих свободных колебаний в отсутствии потерь энергии в колебательной системе. В новых обозначениях дифференциальное уравнение затухающих колебаний имеет вид:

 

.

 

Это линейное дифференциальное уравнение второго порядка. Уравнение затухающих колебаний  есть решение такого дифференциального уравнения:

 

, .

 

В приложении 1 показано получение решения дифференциального уравнения затухающих колебаний методом замены переменных. Частота затухающих колебаний:

(физический смысл имеет только вещественный корень, поэтому ).

Период затухающих колебаний:

 

.

 

Смысл, который вкладывался в понятие периода для незатухающих колебаний, не подходит для затухающих колебаний, так как колебательная система никогда не возвращается в исходное состояние из-за потерь колебательной энергии. При наличии трения колебания идут медленнее: .

Периодом затухающих колебаний называется минимальный промежуток времени, за который система проходит дважды положение равновесия в одном направлении. Для механической системы пружинного маятника имеем:

 

,    .

 

 

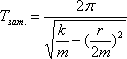Амплитуда затухающих колебаний:

 

,     для пружинного  маятника  .

 

Амплитуда затухающих колебаний – величина не постоянная, а изменяющаяся со временем  тем быстрее, чем больше коэффициент β. Поэтому определение для амплитуды, данное ранее для незатухающих свободных колебаний, для затухающих колебаний надо изменить: при небольших затуханиях амплитудой затухающих колебаний называется наибольшее отклонение от положения равновесия за период.

Графики зависимости смещения от времени    и амплитуды от времени   представлены на Рисунках 3.1 и 3.2.

Рисунок 3.1 – Зависимости амплитуды      Рисунок 3.2 – Зависимость смещения от времени для затухающих колебаний.

 

 

§3.2. Электромагнитные затухающие колебания.

Электромагнитные затухающие колебания возникают в  электромагнитной колебательной систему, называемой  LCR – контур (Рисунок 3.3).

 

 

 

Рисунок 3.3.

Дифференциальное уравнение получим с помощью второго закона Кирхгофа для замкнутого LCR – контура: сумма падений напряжения на активном сопротивлении (R) и конденсаторе (С) равна ЭДС индукции, развиваемой в цепи контура:  

Падение напряжения: - на активном сопротивлении:  , где I – сила тока в контуре; на конденсаторе (С):  , где q – величина заряда  на одной из обкладок конденсатора.

ЭДС, развиваемая в контуре – это ЭДС индукции, возникающая в катушке индуктивности при изменении тока в ней, а следовательно, и магнитного потока сквозь ее сечение:

 

 

(закон Фарадея). Подставим значения U_R, U_C,  в уравнение, отражающее второе правило Кирхгофа, получим:

 

.

 

Сила тока определяется как производная от заряда  ,  тогда  , и дифференциальное уравнение примет вид:

 

.

 

Обозначим  , , получим в этих обозначениях дифференциальное уравнение затухающих колебаний в виде:

 

.

Решение дифференциального уравнения или  уравнение колебаний для заряда на обкладках конденсатора имеет вид:

 

 или .

 

Амплитуда затухающих колебаний  заряда имеет вид:

 

, где .

 

Частота затухающих колебаний в LCR – контуре:

 

.

 

Период затухающих электромагнитных колебаний:

.

 

 

Возьмем уравнение для заряда в виде , тогда уравнение для напряжения на обкладках конденсатора можно записать так

 

.

 

Величина  называется амплитудой напряжения на конденсаторе.

 

Ток в контуре меняется со временем. Уравнение для силы тока в контуре можно получить, используя соотношение  и векторную диаграмму. Окончательное уравнение для силы тока  таково:

 

,

 

где  - начальная фаза. Она не равна α, так как сила тока изменяется не по синусу, что дала бы производная от заряда, а по косинусу.

 

Энергия колебаний в контуре складывается из энергии электрического поля

 

 

и энергии магнитного поля

 

 

Полная энергия в любой момент времени:

 

 

где  W₀ – полная энергия контура в момент времени t=0.