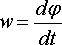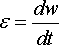- •Физика экзамен т.1 Основы классической механики Кинематика.
- •Механика
- •Т.2 Основы статистической физики и термодинамики Статистическая физика
- •Взаимосвязь кинетической энергии движения молекул и температур Основы термодинамики
- •Т.3 Электростатика
- •Теорема Гаусса для электрической индукции (электрического смещения)
- •Теорема Гаусса для электрической индукции (электрического смещения)[
- •Теорема Гаусса для магнитной индукции
- •Теорема Гаусса для ньютоновской гравитации
- •Т.4 Постоянный электрический ток
- •Т.5 Электромагнетизм
- •Формула 1 — Закон Био Савара Лапласа
- •Формула 2 — определяет модуль вектора dB
- •Т.6. Основы теории Максвелла
- •Т. 7. Физика колебательных процессов
- •§1.1. Механические гармонические колебания.
- •§1.2. Зависимость амплитуды и начальной фазы колебаний от начальных условий.
- •§1.3. Свободные гармонические колебания в lc-контуре.
- •§1.4. Графическое изображение гармонических колебаний. Векторная диаграмма.
- •Глава 2. Сложение гармонических колебаний
- •§2.1. Сложение гармонических колебаний одного направления.
- •§2.2. Сложение взаимно перпендикулярных колебаний.
- •Глава 3. Затухающие колебания.
- •§3.1. Механические затухающие колебания.
- •§3.2. Электромагнитные затухающие колебания.
- •§3.3. Характеристики затухающих колебаний.
- •Глава 4. Вынужденные колебания.
- •§4.1. Общие признаки вынужденных механических и электромагнитных колебаний.
- •§4.2. Зависимости амплитуды вынужденных колебаний и сдвига фаз от частоты внешнего воздействия. Резонанс.
Физика экзамен т.1 Основы классической механики Кинематика.
В кинематике дается математическое описание механического движения тел безотносительно к причинам, обеспечивающим осуществление каждого конкретного вида движения.
Перемещение, скорость и ускорение.
S – Перемещение. Вектор соединяющий, начальную и конечную точки движения.
L – Длина траектории. L и S могут не совпадать
V – Скорость равномерного движения, мгновенная скорость, конечная скорость в равноускоренном движении.
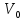 –Начальная
скорость в равноускоренном движении
–Начальная
скорость в равноускоренном движении
А – Ускорение.
S=vt Перемещение при равноМерном движении.
Перемещение при равноУскоренном движении.
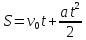


Другие
формулы, где встречается перемещение:
 - Скорость при равноМерном движении.A=FScosa
- Работа силы
- Скорость при равноМерном движении.A=FScosa
- Работа силы
Кинематическое уравнения поступательного движения
При движении тела относительно выбранной системы координат его положение изменяется с течением времени. Движение материальной точки будет полностью определено, если заданы непрерывные и однозначные функции координат от времени: x=x(t), y=y(t), z=z(t) . Эти уравнения называются кинематическими уравнениями движения в координатном виде.
Кинематическое
уравнение движения в векторном виде:  ,
оно
эквивалентно трем координатным
уравнениям. Координатные и векторные
уравнения движения связаны между собой,
т.к. радиус–вектор можно представить
в виде
,
оно
эквивалентно трем координатным
уравнениям. Координатные и векторные
уравнения движения связаны между собой,
т.к. радиус–вектор можно представить
в виде
 .
.
Модуль
радиус–вектора равен 
|
|
Вектором перемещения тела за промежуток времени Δt = t2– t1 называется вектор, проведенный из положения тела в момент времени t1 (точка А на рисунке 1.1.2) в положение в момент времениt2 (точка С). Вектор перемещения равен приращению радиус–вектора за рассматриваемый промежуток времени:
где Δx, Δy, Δz – приращения (изменения) координат точки за рассматриваемый промежуток времени. Модуль вектора приращения равен .
Длина
вектора перемещения
|
|
| |
Рассмотрим
движение материальной точки по
криволинейной плоской траектории. Вектор
скорости в любой точке траектории
направлен по касательной к ней. Допустим,
что в т.М траектории скорость была ![]() ,
а в т.М1 стала
,
а в т.М1 стала ![]() .
При этом считаем, что промежуток времени
при переходе точки на пути
.
При этом считаем, что промежуток времени
при переходе точки на пути![]() из
М в М1 настолько
мал, что изменением ускорения по величине
и направлению можно пренебречь. Для
того, чтобы найти вектор изменения
скорости
из
М в М1 настолько
мал, что изменением ускорения по величине
и направлению можно пренебречь. Для
того, чтобы найти вектор изменения
скорости ![]() ,
необходимо определить векторную
разность:
,
необходимо определить векторную
разность:![]() Для этого перенесем
Для этого перенесем![]() параллельно
самому себе, совмещая его начало с точкой
М. Разность двух векторов равна вектору,
соединяющему их концы
параллельно
самому себе, совмещая его начало с точкой
М. Разность двух векторов равна вектору,
соединяющему их концы![]() равна
стороне АС
равна
стороне АС![]() МАС,
построенного на векторах скоростей,
как на сторонах. Разложим вектор
МАС,
построенного на векторах скоростей,
как на сторонах. Разложим вектор![]() на
две составляющих АВ и АД, и обе
соответственно через
на
две составляющих АВ и АД, и обе
соответственно через![]() и
и![]() .
Таким образом вектор изменения
скорости
.
Таким образом вектор изменения
скорости![]() равен
векторной сумме двух векторов:
равен
векторной сумме двух векторов:
![]()
По
определению:
![]()
Тангенциальное
ускорение ![]() характеризует
быстроту изменения скорости движения
по численному значению и направлена по
касательной к траектории.
характеризует
быстроту изменения скорости движения
по численному значению и направлена по
касательной к траектории.
Следовательно
![]()
Нормальное
ускорение ![]() характеризует
быстроту изменения скорости по
направлению. Вычислим вектор:
характеризует
быстроту изменения скорости по
направлению. Вычислим вектор:
![]()
Для
этого проведем перпендикуляр через
точки М и М1 к касательным к траектории
(рис. 1.4) Точку пересечения обозначим
через О. При достаточно малом ![]() участок
криволинейной траектории можно считать
частью окружности радиуса R. Треугольники
МОМ1 и МВС подобны, потому, что являются
равнобедренными треугольниками с
одинаковыми углами при вершинах. Поэтому:
участок
криволинейной траектории можно считать
частью окружности радиуса R. Треугольники
МОМ1 и МВС подобны, потому, что являются
равнобедренными треугольниками с
одинаковыми углами при вершинах. Поэтому:
![]() или
или
![]() Но
Но![]() ,
тогда:
,
тогда:![]()
Переходя
к пределу при ![]() и
учитывая, что при этом
и
учитывая, что при этом![]() ,
находим:
,
находим:
![]() ;
;
![]()
Полное ускорение определяется векторной суммой тангенциального нормального ускорений. Так как векторы этих ускорений взаимноперпендикулярны, то модуль полного ускорения равен:
![]()
Направление
полного ускорения определяется углом
между векторам ![]() и
и![]() :
:
Вращательное движение
Ускорение вращательного движения тела (угловое ускорение) равно e = dw/dt
Если ускорение с течением времени не изменяется, то e = Dw/Dt, где Dw = w - w0 - разность угловых скоростей в произвольный момент времени t и в момент времени t = 0.
Кинематические угловые характеристики вращательного движения
Вектор углового перемещения.
Вращательное движение абсолютно твердого тела относительно неподвижной оси – движение, при котором все точки тела движутся по окружностям, центры которых лежат на прямой линии, называемой осью вращения. При вращательном движении точки тела, находящиеся на разном расстоянии от оси вращения за одинаковые промежутки времени имеют разные перемещения и имеют разные скорости и ускорения.

В то же время радиус-вектор, соединяющий точки тела с осью вращения, за одинаковые промежутки времени поворачиваются на один и тот же угол Δφ.
Введем понятие вектора углового перемещения. Вектор углового
перемещения Δϕ r - это вектор, определяющий, как вращается твердое тело. Направление вектора Δϕ r определяется правилом правого винта: если головку винта вращать в направлении вращении тела, то направление поступательного движения винта совпадает с направлением вектора Δϕ r.
Если
время вращения бесконечно мало, угловое
перемещение будет dϕ
d – векторная величина (псевдовектор, аксиальный вектор).
Модуль dϕ равен углу поворота.
Направление dϕ определяется правилом правого винта.
Угловая скорость.
Средняя
угловая скорость. 
Пусть
за время Δt тело повернулось на угол Δϕ
. Средняя
угловая скорость – это физическая
величина равная отношению вектора
углового перемещения к промежутку
времени, за который это перемещение
произошло:
![]() Средняя
угловая скорость – это вектор, направление
которого совпадает с вектором Δϕ. Значит,
вектор средней угловой скорости направлен
по оси вращения и определяется правилом
правого винта.
Средняя
угловая скорость – это вектор, направление
которого совпадает с вектором Δϕ. Значит,
вектор средней угловой скорости направлен
по оси вращения и определяется правилом
правого винта.
Угловое ускорение.
Вращение с постоянной угловой скоростью ω = const называется равномерным.
Если угловая скорость ω ≠ const , то тело вращается с угловым ускорением.
Среднее
угловое ускорение
– это физическая величина, равная
отношению вектора изменения угловой
скорости к промежутку времени, за который
это изменение произошло:
![]()
Среднее угловое ускорение – это вектор, направление которого совпадает с направлением Δω .

Мгновенное угловое ускорение – это угловое ускорение вращающегося тела в данный момент времени. Мгновенное угловое ускорение – это физическая величина, равная отношению вектора элементарного изменения угловой скорости к промежутку времени, за который это изменение произошло. Если время движения бесконечно мало 0 t →Δ , то вектор изменения угловой скорости Δω→dω , значит, мгновенное угловое ускорение – это предел, к которому стремится
среднее угловое ускорение при Δt → 0

Таким образом, угловым ускорением называется векторная величина, численно равная первой производной от угловой скорости по времени. Вектор углового ускорения ε направлен вдоль оси вращения в ту сторону, что и ω при ускоренном вращении и в противоположную сторону при замедленном вращении.
Аналогия между поступательным и вращательным движениями
Между движением твердого тела вокруг неподвижной оси и движением отдельной материальной точки (или поступательным движением тела) существует тесная и далеко идущая аналогия. Каждой линейной величине из кинематики точки соответствует подобная величина из кинематики вращения твердого тела. Координате s соответствует угол φ , линейной скорости v - угловая скорость w , линейному (касательному) ускорению а - угловое ускорение ε .
Сравнительные параметры движения:
|
Поступательное движение |
Вращательное движение | |||
|
Перемещение |
S |
Угловое перемещение |
φ | |
|
Линейная скорость |
|
Угловая скорость |
| |
|
Ускорение |
|
Угловое ускорение |
| |
|
Масса |
m |
Момент инерции |
I | |
|
Импульс |
|
Момент импульса |
| |
|
Сила |
F |
Момент силы |
M | |
Работа
|
|
|
Кинетическая энергия
|
|
|
Выражения для вращательного движения напоминают соответствующие выражения поступательного движения. Они получаются из последних формальной заменой m → I , v → w , p → L
Выражения имеют не просто формальное сходство. Поступательное движение можно рассматривать, как вращательное, с радиусом вращения, стремящимся к бесконечности, и угловой скоростью, стремящейся к нулю.


 Рисунок
1.1.2. – Траектория, путь и вектор
перемещения.
Рисунок
1.1.2. – Траектория, путь и вектор
перемещения.

 отличается
при криволинейном движении от длины
пути
отличается
при криволинейном движении от длины
пути тем
больше, чем больше промежуток времениΔt.
При Δt→0
в пределе величина перемещения равна
пути, т.е. Δr→Δs.
тем
больше, чем больше промежуток времениΔt.
При Δt→0
в пределе величина перемещения равна
пути, т.е. Δr→Δs.