fiz / 25-29

25. Зако́н Ампе́ра  — закон взаимодействия электрических токов. Впервые был установлен Андре Мари Ампером в 1820 для постоянного тока. Из закона Ампера следует, что параллельные проводники с электрическими токами, текущими в одном направлении, притягиваются, а в противоположных — отталкиваются. Законом Ампера называется также закон, определяющий силу, с которой магнитное поле действует на малый отрезок проводника с током. Выражение для силы , с которой магнитное поле действует на элемент объёма  проводника с током плотности , находящегося в магнитном поле с индукцией , в Международной системе единиц (СИ) имеет вид:

.

Если ток течёт по тонкому проводнику, то , где  — «элемент длины» проводника — вектор, по модулю равный  и совпадающий по направлению с током. Тогда предыдущее равенство можно переписать следующим образом:

Сила , с которой магнитное поле действует на элемент  проводника с током, находящегося в магнитном поле, прямо пропорциональна силе тока  в проводнике и векторному произведению элемента длины  проводника на магнитную индукцию :

• Ампер есть сила неизменяющегося тока, который при прохождении по двум параллельным прямолинейным проводникам бесконечной длины и ничтожно малой площади кругового поперечного сечения, расположенным в вакууме на расстоянии 1 метр один от другого, вызвал бы на каждом участке проводника длиной 1 метр силу взаимодействия, равную 2·10⁻⁷ ньютона.

Магнитное поле движущегося заряда может возникать вокруг проводника с током. Так как в нем движутся электроны, обладающие элементарным электрическим зарядом. Также его можно наблюдать и при движении других носителей зарядов. Например, ионов в газах или жидкостях. Это упорядоченное движение носителей зарядов, как известно, вызывает в окружающем пространстве возникновение магнитного поля. Таким образом, можно предположить, что магнитное поле независимо от природы тока его вызывающего возникает и вокруг одного заряда находящегося в движении.

 Общее же поле в окружающей среде формируется из суммы полей создаваемых отдельными зарядами. Этот вывод можно сделать исходя из принципа суперпозиции. На основании различных опытов был получен закон, который определяет магнитную индукцию для точечного заряда. Это заряд свободно перемещается в среде с постоянной скоростью.

• 

Формула 1 — закон электромагнитной индукции для движущегося точечного заряда

•  

Где r радиус-вектор, идущий от заряда к точке наблюдения

 Q заряд

 V вектор скорости движения заряда

• 

Формула 2 — модуль вектора индукции

Где альфа это угол между вектором скорости и радиус вектором

 Эти формулы определяют магнитную индукцию для положительного заряда. Если ее необходимо рассчитать для отрицательного заряда то нужно подставить заряд со знаком минус. Скорость движения заряда определяется относительно точки наблюдения.

 Чтобы обнаружить магнитное поле при перемещении заряда можно провести опыт. При этом заряд не обязательно должен двигаться под действием электрических сил. Первая часть опыта состоит в том, что по проводнику круговой формы проходит электрический ток. Следовательно, вокруг него образуется магнитное поле. Действие, которого можно наблюдать при отклонении магнитной стрелки находящейся рядом с витком.

• 

• Рисунок 1 — круговой виток с током воздействует на магнитную стрелку

•  

На рисунке изображён виток с током, слева показана плоскость витка справа плоскость перпендикулярная ей.

Во второй части опыта мы возьмем сплошной металлический диск, закрепленный на оси от которой он изолирован. При этом диску сообщен электрический заряд, и он способен быстро вращаться вокруг своей оси. Над диском закреплена магнитная стрелка. Если раскрутить диск с зарядом, то можно обнаружить что стрелка вращается. Причем это движение стрелки будет таким же, как при движении тока по кольцу. Если при этом изменить заряд диска или направление вращения, то и стрелка будет отклоняться в другую сторону.

• 

Рисунок 2 — вращающийся проводящий заряженный диск

•  

  Из этих опытов можно сделать вывод, что независимо от природы возникновения электрического тока. А также от носителей зарядов, которые его обеспечивают. Магнитное поле возникает вокруг всех движущихся зарядов.

Сила Лоренца — сила, с которой электромагнитное поле согласно классической (неквантовой) электродинамике действует на точечнуюзаряженную частицу. Иногда силой Лоренца называют силу, действующую на движущийся со скоростью  заряд  лишь со стороны магнитного поля, нередко же полную силу — со стороны электромагнитного поля вообще^[1], иначе говоря, со стороны электрического  и магнитного полей. В Международной системе единиц (СИ) выражается как:

26. Циркуляция магнитного поля постоянных токов по всякому замкнутому контуру пропорциональна сумме сил токов, пронизывающих контур циркуляции.

,

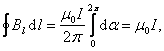 разделе “Электростатика” было доказано, что циркуляция вектора напряженности электростатического поля вдоль замкнутого контура равна нулю, откуда следует потенциальный характер электростатического поля. Одним из основных отличий магнитного поля от электростатического поля является его непотенциальность. Для доказательства этого рассмотрим линейный интеграл от В по замкнутому пути в магнитном поле, создаваемом током, т.е.

где – вектор элемента длины контура, направленный вдоль обхода контура; Вℓ – проекция вектора  на направление касательной к контуру. Данный интеграл называется циркуляцией вектора  по заданному замкнутому контуру ℓ.

27. Соленоид представляет цилиндрический каркас, на который намотаны витки проволоки. Рассмотрим бесконечно длинный соленоид, т.е. соленоид у которого ? >> d, где ? - длина, d – диаметр соленоида. Внутри такого соленоида магнитное поле однородно. Однородным называется поле, силовые линии которого параллельны и густота их постоянна.

 

Применим закон полного тока для вычисления напряженности магнитного поля соленоида. Представим контур L, по которому рассматривается циркуляция вектора , состоящим из четырех связанных участков 1-2; 2-3; 3-4; 4-1. Тогда циркуляция вектора  по выбранному нами контуру L будет равна

.

, т.к.   и, следовательно, ,

, т.к.  мы выбрали участок 3-4 достаточно далеко от соленоида и можно считать, что поле вдали от соленоида равно нулю,

, т.к.   и, следовательно, .

L охватываетN токов, где N – число витков соленоида, тогда по закону полного тока

 ;

 - магнитное поле бесконечно длинного соленоида

n – плотность намотки – число витков на единицу длины .

Тороид – тор, с намотанными на него витками проволоки. В отличие от соленоида, у которого магнитное поле имеется как внутри, так и снаружи, у тороида магнитное поле полностью сосредоточено внутри витков, т.е. нет рассеивания энергии магнитного поля.

,

где .

 – магнитное поле тороида.

Если R >>R_витка, то R ≈r и H = n?.

28.

Магни́тный пото́к — поток  как интеграл вектора магнитной индукции  через конечную поверхность . Определяется через интеграл по поверхности

при этом векторный элемент площади поверхности определяется как

где  — единичный вектор, нормальный к поверхности.

Также магнитный поток можно рассчитать как скалярное произведение вектора магнитной индукции на вектор площади:

где α — угол между вектором магнитной индукции и нормалью к плоскости площади.

Магнитный поток через контур также можно выразить через циркуляцию векторного потенциала магнитного поля по этому контуру:

Теорема гауса:

В соответствии с теоремой Гаусса для магнитной индукции поток вектора магнитной индукции через любую замкнутую поверхность равен нулю:

Или, в дифференциальной форме — дивергенция магнитного поля равна нулю:

Это означает, что в классической электродинамике невозможно существование магнитных зарядов, которые создавали бы магнитное поле подобно тому, как электрические заряды создают электрическое поле.

29.

Рассмотрим контур с током, образованный неподвижными проводами и скользящей по ним подвижной перемычкой длиной l (рис. 2.17). Этот контур находится во внешнем однородном магнитном поле  , перпендикулярном к плоскости контура. При показанном на рисунке направлении тока I, вектор   сонаправлен с  .

Рис. 2.17

      На элемент тока I (подвижный провод) длиной l действует сила Ампера, направленная вправо:

      Пусть проводник l переместится параллельно самому себе на расстояние  dx. При этом совершится работа:

      Итак,

,

   Работа, совершаемая проводником с током при перемещении, численно равна произведению тока на магнитный поток, пересечённый этим проводником.

      Формула остаётся справедливой, если проводник любой формы движется под любым углом к линиям вектора магнитной индукции.

      Выведем выражение для работы по перемещению замкнутого контура с током в магнитном поле.

 Рассмотрим прямоугольный контур с током 1-2-3-4-1 (рис. 2.18). Магнитное поле направлено от нас перпендикулярно плоскости контура. Магнитный поток , пронизывающий контур, направлен по нормали  к контуру, поэтому .

Рис. 2.18

      Переместим этот контур параллельно самому себе в новое положение 1'-2'-3'-4'-1'. Магнитное поле в общем случае может быть неоднородным и  новый контур будет пронизан магнитным потоком .

      Полная работа по перемещению контура в магнитном поле равна алгебраической сумме работ, совершаемых при перемещении каждой из четырех сторон контура:

 равны нулю, т.к. эти стороны не пересекают магнитного потока, при своём перемещение (очерчивают нулевую площадку).

      Провод 1–2 перерезает поток ( ), но движется против сил действия магнитного поля.

      Тогда общая работа по перемещению контура

      Работа, совершаемая при перемещении замкнутого контура с током в магнитном поле, равна произведению величины тока на изменение магнитного потока, сцепленного с этим контуром.

      Элементарную работу по бесконечно малому перемещению контура в магнитном поле можно найти по формуле

,

(2.9.5)

      Выражения (2.9.1) и (2.9.5) внешне тождественны, но физический смысл величины dФ различен.

      Соотношение (2.9.5), выведенное нами для простейшего случая, остаётся справедливым для контура любой формы в произвольном магнитном поле. Более того, если контур неподвижен, а меняется , то при изменении магнитного потока в контуре на величину dФ, магнитное поле совершает ту же работу