1) Механика – раздел физики изучающий механические движения, а также причины вызывающие или изменяющие эти движения. Механическое движение - это изменение положения тела с течением времени.

Система отсчёта — это совокупность тела отсчета, связанной с ним системы координат и системы отсчёта времени, по отношению к которым рассматривается движение (или равновесие) каких-либо материальных точек или тел.

Траектория материальной точки - линия в пространстве, представляющая собой множество точек, в которых находилась, находится или будет находиться материальная точка при своём перемещении в пространстве относительно выбранной системы отсчёта.  Если траектория - прямая линия, то движение называется прямолинейным, в противном случае - криволинейным.

Радиус-вектор - вектор, задающий положения точки в пространстве относительно некоторой заранее фиксированной точки, называемой началом координат.

Перемещение - изменение местоположения физического тела в пространстве относительно выбранной системы отсчёта. Также перемещением называют вектор, характеризующий это изменение.

Путь - длина участка траектории материальной точки. (Путь, пройденный за единицу времени).

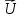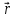Скорость - векторная физическая величина, характеризующая быстроту перемещения и направление движения материальной точки относительно выбранной системы отсчёта. (По определению, равна производной радиус-вектора точки по времени). (=d/dt)

Ускорение - векторная величина, характеризующая быстроту изменения скорости точки по её численному значению и по направлению. (=d/dt)

2) Угловое перемещение - векторная величина, характеризующая изменение угловой координаты в процессе её движения.

Угловая скорость - векторная величина, характеризующая быстроту вращения материальной точки. Вектор направлен вдоль оси вращения таким образом, чтобы, смотря с его конца, вращение казалось происходящим против часовой стрелки. (=dφ/dt)

Угловое ускорение - псевдовекторная физическая величина, характеризующая быстроту изменения угловой скорости материальной точки.(=d/dt)

Аналогия и взаимосвязь хар-ки поступательного и вращательного движения:

Поступательное Вращательное Взаимосвязь

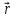, dr d

S φ S=Rφ

=d/dt =d/dt =[, ]

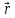U=dS/dt ω=dφ/dt U=ω

=d/dt =d/dt =[;]+[;]

a=dU/dt β=dω/dt a=Rβ

a_n=[;]

3)

4) Первый закон Ньютона - всякое тело пребывает в состоянии покоя или равномерного прямолинейного движения до тех пор, пока действующие на него силы не изменят это состояние.

Второй закон Ньютона - ускорение, приобретаемое телом в результате воздействия на него, прямо пропорционально силе или равнодействующей сил этого воздействия и обратно пропорционально массе тела. (=/m, где - ускорение тела, - сила, приложенная к телу, m – масса материальной точки)

Формулировка Второго закона Ньютона с использованием импульса - в инерциальных системах отсчёта производная импульса материальной точки по времени равна действующей на него силе. (d/dt=F, где =m импульс, – скорость, t - время)

Третий закон Ньютона - силы, с которыми два тела действуют друг на друга, равны по величине и противоположны по направлению. (F₁=-F₂)

Импульс - векторная физическая величина, равная произведению массы этого тела на его скорость.

Импульс силы — это векторная физическая величина, равная произведению силы на время её действия, мера воздействия силы на тело за данный промежуток времени (в поступательном движении)(=).

Сила — векторная физическая величина, являющаяся мерой интенсивности воздействия на данное тело других тел, а также полей, в результате которого тело приобретает ускорение или изменяет свою форму или размеры.

Масса - скалярная физическая величина, являющаяся одной из характеристик материи определяющая её инерционный и гравитационные свойства.

5) Момент силы - векторная физическая величина, равная векторному произведению радиус-вектора, на вектор этой силы. (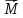=[ x ], - сила, действующая на частицу, - радиус-вектор частицы)

Момент импульса - векторное произведение радиус-вектора материальной точки на её импульс. (=[ x ])

6) Моментом инерции механической системы относительно неподвижной оси («осевой момент инерции») называется величина J_a, равная сумме произведений масс всех n материальных точек системы на квадраты их расстояний до оси. (J_a=)

Теорема Гюйгенса - Штейнера - момент инерции J тела относительно произвольной оси равен сумме момента инерции этого тела J_c относительно параллельной ей оси, проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния d между осями. (J=J_c+md²⁾

Где J_c — известный момент инерции относительно оси, проходящей через центр масс тела, J — искомый момент инерции относительно параллельной оси, m — масса тела, d — расстояние между указанными осями.

Основной закон динамики вращательного движения - произведение момента инерции на угловое ускорение равно результирующему моменту сил, действующих на материальную точку. (dt=d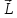, изменение момента количества движения твердого тела d, равно импульсу момента dt всех внешних сил, действующих на это тело)

7)1. Если на тело действует постоянная сила F, и это приводит к перемещению ∆ r тела, то элементарной работой ∆А постоянной силы называется скалярное произведение вектора силы F и вектора перемещения ∆r.(∆А = (F∙∆r) = ½ F½½∆ r½ cos·a, где a - угол между направлениями векторов силы F и перемещения ∆r, (F∙ ∆r) – скалярное произведение двух векторов).

Работа ∆А - скаляр. Если угол a - острый, то ∆А положительная величина, и говорят, что сила совершает работу. Если угол a - тупой, то ∆А - отрицательная величина, и говорят, что работа совершается против действия силы. Если a = 90⁰, т.е. направления силы и перемещения взаимно перпендикулярны, то такая сила работы не совершает ∆А = 0. Такая сила не может изменить величину скорости тела, но она меняет направление скорости.

2. Работа переменной силы. Если сила или равнодействующая сил изменяет свою величину или направление (движение по криволинейной траектории, причем угол α ≠ 90⁰), то работа ∆А, совершаемая переменной силой F (или Fрез) на конечном участке траектории вычисляется следующим образом. На рисунке представлен график зависимости силы F от пути S. Разобьем весь путь на N участков. Перемещение и действующая сила на каждом участке соответственно равны F _i и ∆ r _i. Тогда работа А, совершаемая силой F, равна алгебраической сумме работ, совершаемых каждой из сил F _i на своем малом участке:

А = ∆А₁ + ∆А₂ +....+ ∆А _N = ( F₁∙∆ r₁) + (F ₂∙∆ r₂) + ...+( F _N∙∆ r_N) =  ( F_i∙∆ r_i), где i = 1,2...... N - номер элементарного участка траектории. На участке ∆r _i силу F_i можно считать постоянной, тогда элементарная работа ∆А_i на участке ∆r _iравна ∆А_i= F_i∙∆ r _i и равна площади заштрихованной фигуры на рисунке.А=∆А_i - это работа силы F на участке r, равна она численно площади S фигуры, ограниченной кривой зависимости F(х) и осью Х.

3. Рассмотрим действие внешней силы , приложенной к точке массой . За время  элементарная масса  проходит путь  Работа силы  на этом пути определяется проекцией силы на направление перемещения, которая очевидно, равна тангенциальной составляющей  силы.

Но  равна модулю момента  силы  относительно оси вращения. Работа , и будет положительна, если  имеет такое же направление, как и  отрицательное, если направление векторов  и  противоположны.

С учетом, что  то

Работа всех сил, приложенных к телу

Полная работа

8) Кинетическая энергия - энергия механической системы, зависящая от скоростей движения её точек в выбранной системе отсчёта.

Кин. Энергия вращ. Тела: Кинетическая энергия тела, движущегося произвольным образом, равна сумме кинетических энергий всех n материальных точек па которые это тело можно разбить:

Если тело вращается вокруг неподвижной оси с угловой скоростью , то линейная скорость i-ой точки равна , где , - расстояние от этой точки до оси вращения. Следовательно.

где  - момент инерции тела относительно оси вращения.

В общем случае движение твердого тела можно представить в виде суммы двух движений - поступательного со скоростью, равной скорости  центра инерции тела, и вращения с угловой скоростью вокруг мгновенной оси, проходящей через центр инерции. При этом выражение для кинетической энергии тела преобразуется к виду

где  - момент инерции тела относительно мгновенной оси вращения, проходящей через центр инерции.

 Теперь рассмотрим связь кинетической энергии с работой.         Если постоянная сила действует на тело, то оно будет двигаться в направлении силы. Тогда элементарная работа по перемещению тела из точки 1 в точку 2, будет равна произведению силы F на перемещение dr :

dA = F dr,  отсюда  ,         ,

Окончательно получаем:

.

Следовательно, работа силы, приложенной к телу на пути r, численно равна изменению кинетической энергии этого тела: A=ΔK

Или изменение кинетической энергии dK равно работе внешних сил: dK = dA.

9) Консервативные силы (потенциальные силы) - это силы, работа которых не зависит от вида траектории точки приложения этой силы и закона её движения и определяется только начальным и конечным положением этой точки. Равносильным определением является и следующее: консервативные силы - это такие силы, работа которых по любой замкнутой траектории равна 0.

Потенциальная энергия - скалярная физическая величина, представляющая собой часть полной механической энергии системы, находящейся в поле консервативных сил. Зависит от положения материальных точек, составляющих систему, и характеризует работу, совершаемую полем при их перемещении.

Связь потенциальной энергии и консервативной силы: F = -grad(U) (Где F - консервативная сила, U - потенциальная энергия.)

10) Электрический заряд (q) — это физическая скалярная величина, определяющая способность тел быть источником электромагнитных полей и принимать участие в электромагнитном взаимодействии.

Закон сохранения электрического заряда: Электрический заряд замкнутой системы сохраняется во времени и квантуется - изменяется порциями, кратными элементарному электрическому заряду, то есть, другими словами, алгебраическая сумма электрических зарядов тел или частиц, образующих электрически изолированную систему, не изменяется при любых процессах, происходящих в этой системе.

В рассматриваемой системе могут образовываться новые электрически заряженные частицы, например, электроны - вследствие явления ионизации атомов или молекул, ионы - за счёт явления электролитической диссоциации и др. Однако, если система электрически изолирована, то алгебраическая сумма зарядов всех частиц, в том числе и вновь появившихся в такой системе, всегда равна нулю.

Закон Кулона: Сила взаимодействия двух точечных зарядов в вакууме направлена вдоль прямой, соединяющей эти заряды, пропорциональна их величинам и обратно пропорциональна квадрату расстояния между ними. Она является силой притяжения, если знаки зарядов разные, и силой отталкивания, если эти знаки одинаковы.

Важно отметить, что для того, чтобы закон был верен, необходимы:

1. Точечность зарядов, то есть расстояние между заряженными телами должно быть много больше их размеров. Впрочем, можно доказать, что сила взаимодействия двух объёмно распределённых зарядов со сферически симметричными непересекающимися пространственными распределениями равна силе взаимодействия двух эквивалентных точечных зарядов, размещённых в центрах сферической симметрии;

2. Их неподвижность. Иначе вступают в силу дополнительные эффекты: магнитное поле движущегося заряда и соответствующая ему дополнительная сила Лоренца, действующая на другой движущийся заряд;

3. Расположение зарядов в вакууме.

Векторный вид:

где  — сила, с которой заряд 1 действует на заряд 2;  - величина зарядов;  — радиус-вектор (вектор, направленный от заряда 1 к заряду 2, и равный, по модулю, расстоянию между зарядами — );  — коэффициент пропорциональности.

Взаимодействие зарядов: Электрические заряды взаимодействуют между собой, т.е. одноименные заряды взаимно отталкиваются, а разноименные при­тягиваются. Силы взаимодействия электрических зарядов определяются законом Кулона и направлены по прямой линии, соединяю­щей точки, в которых сосредоточены заряды.

Согласно закону Кулона, сила взаимодействия двух точечных электрических зарядов прямо пропорциональна произведению количеств электричества в этих зарядах, обратно пропорциональна квадрату расстояния между ними и зависит от среды, в которой находятся заряды:

 

где F — сила взаимодействия зарядов, н (ньютон),

q₁,  q₂, — количество  электричества   каждого  заряда, к (кулон),

r — расстояние между зарядами, м,

e_a— абсолютная   диэлектрическая проницаемость   среды   (ма­териала); эта величина характеризует электрические свой­ства той среды, в которой находятся взаимодействующие заряды.

Напряженность- векторная физическая величина, характеризующая электрическое поле в данной точке и численно равная отношению силы  действующей на неподвижный пробный заряд, помещенный в данную точку поля, к величине этого заряда q: =/q

11) Принцип суперпозиции - Напряжённость поля, создаваемого системой неподвижных точечных зарядов q₁, q₂, q₃, ¼, q_n, равна векторной сумме напряжённостей электрических полей, создаваемых каждым из этих зарядов в отдельности:                                           

(где r_i – расстояние между зарядом q_i и рассматриваемой точкой поля)

Напряженность поля точечного заряда. Используя закон Кулона найдем выражение для напряжённости электрического поля, создаваемого точечным зарядом q в однородной изотропной среде на расстоянии r от заряда:

  

В этой формуле r – радиус-вектор, соединяющий заряды q и q_пр. Из формулы выше следует, что напряжённость E поля точечного заряда q во всех точках поля направлена радиально от заряда при q > 0 и к заряду при q < 0.

Эквипотенциальные поверхности: Поверхность, во всех точках которой потенциал электрического поля имеет одинаковые значения. Между двумя любыми точками на эквипотзенциальной поверхности разность потенциалов равна нулю, поэтому работа сил электрического поля при любом перемещении заряда по эквипотенциальной поверхности равна нулю. Это означает, что вектор силы 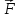 в любой точке траектории движения заряда по эквипотенциальной поверхности перпендикулярен вектору скорости. Следовательно, линии напряженности электростатического поля перпендикулярны эквипотенциальной поверхности.

Эквипотенциальными поверхностями поля точечного электрического заряда являются сферы, в центре которых расположен заряд (рис. 112).

Эквипотенциальные поверхности однородного электрического поля представляют собой плоскости, перпендикулярные линиям напряженности (рис. 113).