Билет 23

Магни́тное по́ле — силовое поле, действующее на движущиеся электрические заряды и на тела, обладающие магнитным моментом, независимо от состояния их движения^[1], магнитная составляющая электромагнитного поля^[2].

Магнитное поле может создаваться током заряженных частиц и/или магнитными моментами электронов в атомах (и магнитными моментами других частиц, хотя в заметно меньшей степени) (постоянные магниты).

Кроме этого, оно появляется при наличии изменяющегося во времени электрического поля.

Основной силовой характеристикой магнитного поля является вектор магнитной индукции  (вектор индукции магнитного поля)^[3][4]. С математической точки зрения  — векторное поле, определяющее и конкретизирующее физическое понятие магнитного поля. Нередко вектор магнитной индукции называется для краткости просто магнитным полем (хотя, наверное, это не самое строгое употребление термина).

Ещё одной фундаментальной характеристикой магнитного поля (альтернативной магнитной индукции и тесно с ней взаимосвязанной, практически равной ей по физическому значению) является векторный потенциал.

• Нередко в литературе в качестве основной характеристики магнитного поля в вакууме (то есть в отсутствие магнитной среды) выбирают не вектор магнитной индукции 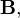а вектор напряжённости магнитного поля , что формально можно сделать, так как в вакууме эти два вектора совпадают^[5]; однако в магнитной среде вектор  не несет уже того же физического смысла^[6], являясь важной, но всё же вспомогательной величиной. Поэтому при формальной эквивалентности обоих подходов для вакуума, с систематической точки зрения следует считать основной характеристикой магнитного поля именно 

Магнитное поле можно назвать особым видом материи^[7], посредством которого осуществляется взаимодействие между движущимися заряженными частицами или телами, обладающими магнитным моментом.

Магнитные поля являются необходимым (в контексте специальной теории относительности) следствием существования электрических полей.

Вместе, магнитное и электрическое поля образуют электромагнитное поле, проявлениями которого являются, в частности, свет и все другие электромагнитные волны.

Единицы измерения

Величина B в системе единиц СИ измеряется в теслах, в системе СГС в гауссах.

Векторное поле H измеряется в амперах на метр (А/м) в системе СИ и в эрстедах в СГС. Эрстеды и гауссы являются тождественными величинами, их разделение является чисто терминологическим.

Вектор магнитной индукции

Магни́тная инду́кция  — векторная величина, являющаяся силовой характеристикой магнитного поля (его действия на заряженные частицы) в данной точке пространства. Определяет, с какой силой  магнитное поле действует на заряд , движущийся со скоростью .

Более конкретно,  — это такой вектор, что сила Лоренца , действующая со стороны магнитного поля^[1] на заряд , движущийся со скоростью , равна

где косым крестом обозначено векторное произведение, α — угол между векторами скорости и магнитной индукции (направление вектора  перпендикулярно им обоим и направлено по правилу буравчика).

Также магнитная индукция может быть определена^[2] как отношение максимального механического момента сил, действующих на рамку с током, помещенную в однородное поле, к произведению силы тока в рамке на её площадь.

Является основной фундаментальной характеристикой магнитного поля, аналогичной вектору напряжённости электрического поля.

В системе СГС магнитная индукция поля измеряется в гауссах (Гс), в системе СИ — в теслах (Тл)

1 Тл = 10⁴ Гс

Магнитометры, применяемые для измерения магнитной индукции, называют тесламетрами.

Основные уравнения

Поскольку вектор магнитной индукции является одной из основных фундаментальных физических величин в теории электромагнетизма, он входит в огромное множество уравнений, иногда непосредственно, иногда через связанную с нимнапряженность магнитного поля. По сути, единственная область в классической теории электромагнетизма, где он отсутствует, это пожалуй разве только чистая электростатика.

• (Здесь формулы приведем в системе единиц СИ, в виде для вакуума^[3], где есть варианты для вакуума — для среды; запись в другом виде и подробности — см. по ссылкам).

В магнитостатике

В магнитостатическом пределе^[4] наиболее важными являются:

• Закон Био-Савара — занимающий в магнитостатике место, занимаемое в электростатике законом Кулона:

• Теорема Ампера о циркуляции магнитного поля^[5]:

В общем случае

Основные уравнения (классической) электродинамики общего случая (то есть независимо от ограничений магнитостатики), в которых участвует вектор магнитной индукции :

• Три из четырех уравнений Максвелла (основных уравнений электродинамики)

• а именно:

• Закон Гаусса для магнитного поля,

• Закон электромагнитной индукции:

• Закон Ампера - Максвелла.

• Формула силы Лоренца

• Следствия из неё, такие как

  • Выражение для силы Ампера, действующей со стороны магнитного поля на ток (участок провода с током)

• выражение для вращающего момента, действующего со стороны магнитного поля на магнитный диполь (виток с током, катушку или постоянный магнит):

• выражение для потенциальной энергии магнитного диполя в магнитном поле:

• а также следующих из них выражения для силы, действующей на магнитный диполь в неоднородном магнитном поле и т. д..

• Выражение для силы, действующей со стороны магнитного поля на точечный магнитный заряд:

• (это выражение, точно соответствующее обычному закону Кулона, широко используется для формальных вычислений, для которых ценна его простота, несмотря на то, что реальных магнитных зарядов в природе не обнаружено; также может прямо применяться к вычислению силы, действующей со стороны магнитного поля на полюс длинного тонкого магнита или соленоида).

• Выражение для плотности энергии магнитного поля

• Оно в свою очередь входит (вместе с энергией электрического поля) и в выражение для энергии электромагнитного поля и в лагранжиан электромагнитного поля и в его действие. Последнее же с современной точки зрения является фундаментальной основой электродинамики (как классической, так в принципе и квантовой).

Напряжённость магни́тного по́ля 

Напряжённость магни́тного по́ля (стандартное обозначение Н) — векторная физическая величина, равная разности вектора магнитной индукции B и вектора намагниченности M.

В Международной системе единиц (СИ):  где  — магнитная постоянная.

В системе СГС: 

• В простейшем случае изотропной (по магнитным свойствам) среды и в приближении достаточно низких частот изменения поля B и H просто пропорциональны друг другу, отличаясь просто числовым множителем (зависящим от среды) B = μ H в системе СГС или B = μ₀μ H в системе СИ (см. Магнитная проницаемость, также см. Магнитная восприимчивость).

В системе СГС напряжённость магнитного поля измеряется в эрстедах (Э), в системе СИ — в амперах на метр (А/м). В технике эрстед постепенно вытесняется единицей СИ — ампером на метр.

1 Э = 1000/(4π) А/м ≈ 79,5775 А/м.

1 А/м = 4π/1000 Э ≈ 0,01256637 Э.