2.5.7 Импульсные трансформаторы

Особенностью работы импульсных трансформаторов является то, что входной сигнал – однополярные импульсы и, в отличие от широкополосных трансформаторов, сердечник работает с постоянным подмагничиванием. Рассмотрим работу импульсного трансформатора, схема включения которого приведена на рис.2.39а, а на рис 2.39б – наиболее характерные эпюры.

Рисунок 2.39 – Схема включения (а) и эпюры для (б) импульсного

трансформатора

Если на вход поступает сигнал е(t), то индукция линейно нарастает на интервале и спадает на интервале () со скоростью, определяемой постоянной времени . Перепад индукции в сердечнике равен

(2.51)

Рабочая точка на петле гистерезиса перемещается по частному циклу перемагничивания, как показано на рисунке 2.40.

Рисунок 2.40 – Перемещение рабочей точки в сердечнике импульсного

трансформатора

Напряжение на нагрузке U₂ имеет отрицательный выброс, так как в сердечнике накапливается энергия (ток намагничивания ). Ток первичной обмотки – трапецеидальный, поскольку к прямоугольному току нагрузки добавляется линейный ток намагничивания сердечника.

На интервале напряжение на входе постоянно и равно . Тогда

, (2.52)

где – потокосцепление

s – сечение магнитопровода.

Так как производная неизменна, то индукция нарастает линейно. Переходим к конечным приращениям и получаем

, (2.53)

где

Тогда выражение (2.53) переписываем в виде

. (2.54)

Выражение (2.54) показывает площадь импульса, передаваемого в нагрузку – основной параметр импульсного трансформатора и чем она больше, тем лучше. Поэтому, чем больше перепад индукции , тем больше площадь импульса.

Индуктивность первичной обмотки определяется магнитной проницаемостью

; (2.55)

Она и определяет основную индуктивность трансформатора. Поэтому на кривой намагничивания предпочтительным является участок с максимальным μ_а. Остаточная индукция В_r должна быть возможно меньшей. Из магнитных материалов лучше всего подходят тонкие ленты трансформаторных сталей и пермаллой с малым коэффициентом прямоугольности . Реже используются ферриты, поскольку они обладают низкой индукцией, хотя и малыми динамическими потерями.

2.6 Примеры задач с решениями

Пример 2.6.1

Исходные данные: Индукция в сердечнике трансформатора В_m =1,0 Тл, число витков первичной обмотки W₁ =1000, приложенное напряжение – меандр U₁ =100 В с частотой 1кГц.

Определите необходимую площадь сечения магнитопровода.

Решение. Воспользуемся уравнением трансформаторной ЭДС для прямоугольной формы напряжения: . Откуда находим

Пример 2.6.2

Исходные данные: Максимальная индукция в сердечнике из феррита равна В_m =0,38 Тл при напряженности Н = 25 А/м, число витков первичной обмотки W =800, поперечное сечение магнитопровода s_с=0,19 см², средняя длина магнитной силовой линии ,частота приложенного напряжения (меандра) f =10 кГц,.

Определите предельные значения тока холостого хода I₁₀ , напряжения U₁ и изобразите зависимость .

Решение. Из уравнения трансформаторной ЭДС следует: . Предельное значение тока холостого хода –

.

Учитывая характер и то, что , а , зависимость намагничивающего тока трансформатора от приложенного напряжения имеет примерно квадратичный характер (рисунок 2.41).

Рисунок 2.41 – Зависимость тока намагничивания от напряжения

Пример 2.6.3

Исходные данные: Зависимость магнитного потока от времени Ф(t) показана на рисунке 2.42.

Рисунок 2.42 – Зависимость магнитного потока от времени Ф(t)

Изобразите зависимость ЭДС от времени.

Решение. Учитывая закон электромагнитной индукции , определим Е(t) раздельно по участкам. На участке [0…t₁] функция линейна и скорость (производная) постоянна: . Тогда . На участке [t₁…t₂] поэтому . На интервале [t₂…t₃], повторяется участок [0…t₁], но с другим знаком. На участке [t₃…t₄] имеет место гармонический закон изменения потока, поэтому получаем ортогональную функцию. Результирующая зависимость Е(t) изображена на рисунке 2.43.

Рисунок 2.43 – Зависимость ЭДС от времени

Пример 2.6.4

Исходные данные: ЭДС первичной обмотки трансформатора изменяется во времени, как показано на рисунке 2.44.

Рисунок 2.44 – Зависимость ЭДС от времени

Изобразите временную зависимость магнитного потока Ф(t).

Решение. Согласно закону электромагнитной индукции для конечных приращенийнаходим: . На участке [t₀…t₁] с учётом знака ЭДС, график будет убывающим. Таким образом, кривая магнитного потока Ф(t) имеет вид, как показано на рисунке 2.45.

Рисунок 2.45 –Зависимость магнитного потока от времени

Пример 2.6.5.

Исходные данные: В однофазном трансформаторе при КПД=0,95 и коэффициенте загрузки , выходная мощностьP₂ =190 Вт.

Определите потери в обмотках.

Решение. КПД трансформатора . При оптимальном коэффициенте загрузки, P_C = P_ОБ (рис.2.28). Решим относительно Р_ОБ.

Следовательно,

Пример 2.6.6

Исходные данные: В результате проведения опыта короткого замыкания трансформатора с отношением витков W₁/W₂=5, найдено Rкз = 10 Ом.

Определите сопротивления потерь первичной и вторичной обмоток.

Решение. Схема замещения трансформатора в опыте КЗ имеет вид, как показано на рисунке 2.46.

Рисунок 2.46 – Схема замещения трансформатора в опыте КЗ

Из определения коэффициента трансформации следует, что W₁/W₂= n=5.

В оптимальном трансформаторе имеет место: Следовательно, .

Пример 2.6.7

Исходные данные: В схеме замещения трансформатора (рисунок 2.47) имеет место U_1ном=141В, U_кз=10%, , .

Определите номинальный ток первичной обмотки трансформатора.

Рисунок 2.47 – Схема замещения трансформатора

Решение. Определим внутреннее сопротивление трансформатора:

, ,.

В опыте КЗ на вход подаётся пониженное напряжение: . Тогда номинальный ток равен .

Пример 2.6.8

Исходные данные: Трансформатор выполнен на броневом сердечнике (рисунок 2.48). Все обмотки равны W₁=W₂=W₃. К обмотке W₁ подведено напряжение U₁=100В.

Определите напряжения U₂ и U₃._.

Рисунок 2.48 – Трансформатор

Решение. В сердечнике трансформатора основной магнитный поток делится на две части, которые пронизывают свои обмотки W₂ и W₃. Из уравнения трансформаторной ЭДС: следует, что основной магнитный поток прямо пропорционален напряжению, следовательно,U₂ =U₃ =

= 50 В.

Пример 2.6.9

Исходные данные: В стержневой однофазный трансформатор (рисунок 2.49) вводится магнитный шунт.

Определите как изменится выходное напряжение трансформатора (U₂) на холостом ходу при введении магнитного шунта.

Рисунок 2.49 – Введение магнитного шунта

Решение. Вследствие введения магнитного шунта, появляется ещё один путь для магнитного потока (см. рисунок 2.50), что приведёт к уменьшению потока Ф ₀ и уменьшению напряжения U₂ пропорционально магнитным сопротивлениям.

Рисунок 2.50 – Влияние магнитного шунта

Пример 2.6.10

Исходные данные: Потери в магнитопроводе трансформатора составляют Pст = 10 Вт; соотношение витков – W1/W2= 1; активные сопротивления обмоток r₁ = r₂ = 0,2 Ом.

Определите при каком токе нагрузки I₂ КПД трансформатора будет максимальным?

Решение. КПД трансформатора максимален, когда Р_СТ =Р_ОБ . Коэффициент трансформации n=1. Поэтому Р_СТ =I₂²*r_к , где . Тогда.

Пример 2.6.11

Исходные данные: Из опыта холостого хода трансформатора получено: U₁хx=220В; I₁xx=0,4A; P₁xx=16Вт.

Определите активное сопротивление цепи намагничивания в схеме замещения трансформатора.

Решение. В опыте холостого хода схема замещения трансформатора имеет вид (рисунок 2.51):

Рисунок 2.51 – Схема замещения трансформатора в опыте ХХ

Пренебрегая потерями и индуктивностью рассеяния, получим

.

Пример 2.6.12

Исходные данные: В трансформаторе при питании от сети с напряжением 220 В и частотой сети f=50 Гц потери в магнитопроводе составляют Р_СТ =20 Вт.

Определите потери в магнитопроводе, если этот трансформатор включить в сеть с частотой 400 Гц и напряжением 110 В (зависимость потерь от частоты и индукции принять квадратичной).

Решение. Магнитная индукция пропорциональна напряжению, а потери зависят от индукции и частоты согласно выражению (2.2) . Следовательно,

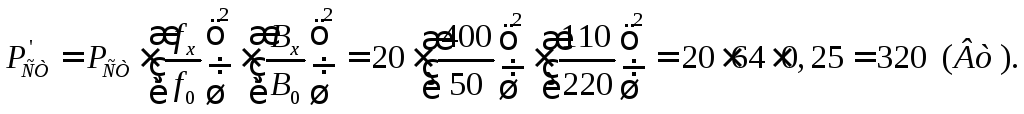
Пример 2.6.13

Исходные данные: Первичная обмотка трёхфазного трансформатора соединена звездой.

Определите во сколько раз изменятся потери в магнитопроводе, если первичную обмотку трёхфазного трансформатора переключить на треугольник.

Решение. При соединении обмоток треугольником к каждой фазной обмотке трансформатора прикладывается линейное напряжение (U_л), которое больше фазного (Uф) в раз.

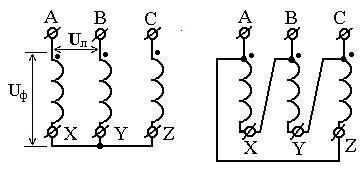
Рисунок 2.52 – Схема соединения обмоток звездой и треугольником

Потери в магнитопроводе зависят от индукции и частоты согласно выражению (2.2 ) .

При переходе на соединение треугольником напряжение, прикладываемое к фазной обмотке увеличивается в раз, что приведёт к увеличению магнитной индукции в раз, а потери возрастут в 3 раза.