
- •Оглавление
- •Предисловие
- •1. Множества. Числa. Действия над числами Множества. Операции над множествами
- •A и b - граничные точки конечного интервалаТабл. 6
- •Сокращение и расширение дроби:
- •Разделение отрезка длиной а на два отрезка х и а – х называется золотым сечением, если х – среднее геометрическое между а и а – х: ;
- •2. Степени, корни, многочлены
- •Операции со степенями и их свойства Табл. 12
- •Операции с корнями и их свойстваТабл. 13
- •3. Последовательности и суммы
- •4. Логарифмирование
- •Десятичные и натуральные логарифмы
- •5. Уравнения
- •6. Неравенства
- •7. Тригонометрия
- •2) ; 3) .
- •Приведение обратных тригонометрических функций:
- •Простейшие тригонометрические уравнения и их решение
- •8. Функции
- •9. Планиметрия
- •Подобия в прямоугольном треугольнике: ;;
- •С Рис. 39войства трапеции:
- •10. Стереометрия
- •Правильные многогранники
2) ; 3) .
П роизведение
тригонометрических функций:
роизведение
тригонометрических функций:
|
|
|
|
| |
|
|
|
|
| |
Обратные тригонометрические функции
Определение обратных тригонометрических функций Табл. 29
|
Наименование |
Обозначение |
Область определения |
Множество значений |
Равносильное равенство |
|
Арксинус |
|
|
|
|
|
Арккосинус |
|
|
|
|
|
Арктангенс |
|
|
|
|
|
Арккотангенс |
|
|
|
|
Основные значения обратных тригонометрических функций Табл. 30
|
a |
0 |
|
|
|
1 |
|
a |
0 |
|
1 |
|
|
arcsin a |
0 |
|
|
|
|
|
arctg a |
0 |
|
|
|
|
arccos a |
|
|
|
|
0 |
|
arcctg a |
|
|
|
|
Приведение обратных тригонометрических функций:
|
|
|
|
|
|
Связь
между обратными тригонометрическими
функциями (при
![]() ):
):
-
 ;
; ;
; ;
; ;
;При
 :
: ;
; .
.
Простейшие тригонометрические уравнения и их решение
![]() -
целое число (
-
целое число (![]() )Табл.
31
)Табл.
31
|
Уравнение |
|
Решение |
Частные случаи | |
|
|
|
|
|
|
|
|
| |||
|
|
| |||
|
|
Нет решений | |||
|
|
|
|
|
|
|
|
| |||
|
|
| |||
|
|
Нет решений | |||
|
|
a – любое число |
|
|
|
|
|
| |||
|
|
| |||
|
|
a – любое число |
|
|
|
|
|
| |||
|
|
| |||
8. Функции
Определение и основные свойства функций
Функция
![]() есть соответствие между множествомХ
и множеством
есть соответствие между множествомХ
и множеством
![]() ,
при котором каждому элементу
,
при котором каждому элементу![]() соответствует единственный элемент
соответствует единственный элемент![]() .
.
X – область определения функции; Y – область изменения функции;
x – аргумент функции; y – значение функции.
Способы задания функции: аналитический, табличный, графический.
График
функции
![]() есть множество точек на плоскости,
есть множество точек на плоскости,
координаты
которых удовлетворяют соотношению
![]() .
.
Простейшие свойства функций Табл. 32
|
Наименование |
Содержание |
|
Четность |
|
|
Нечетность |
|
|
Периодичность |
|
|
Ограниченность |
|
Основные элементарные функции
Классификация основных элементарных функций Табл. 33
|
Название |
Формула |
Частные случаи |
|
Постоянная |
|
|
|
Степенная функция |
|
|
|
Показательная функция |
|
|
|
Логарифмическая функция |
|
|
|
Тригонометрические функции |
| |
|
Обратные тригонометрические функции |
| |
Линейная функция
О бщий
случай:
бщий
случай:![]() .
.
График функции – прямая линия.
![]() - угловой коэффициент
прямой
- угловой коэффициент
прямой
![]() ,
,
![]() - угол, образованный
осью Ox
и прямой,
- угол, образованный
осью Ox
и прямой,
b – отрезок, отсекаемый прямой на оси Oy.
Простейший
случай
![]() .
.
О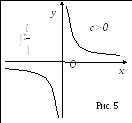
 братная
пропорциональность
братная
пропорциональность
О
Рис.
4![]() .
.
График функции – гипербола.
Квадратичная функция
Общий
вид ![]()
График
функции – парабола.
![]() - дискриминант
- дискриминант
|
Случай
|
|
|
|
|
Случай
|
Рис.
7 |
|
|
Простейший
случай:
![]()
 Рис. 8
Рис. 8
Показательная и логарифмическая функции
Показательная
функция: ![]() .
.
График функции – экспонента.
|
|
|
Логарифмическая
функция: ![]() .
.
График функции – логарифмика.
|
|
|
|
Рис. 11 |
Рис. 12 |
Тригонометрические функции
|
x y
|
|
|
Обратные тригонометрические функции
|
График
арксинуса
Рис. 15 |
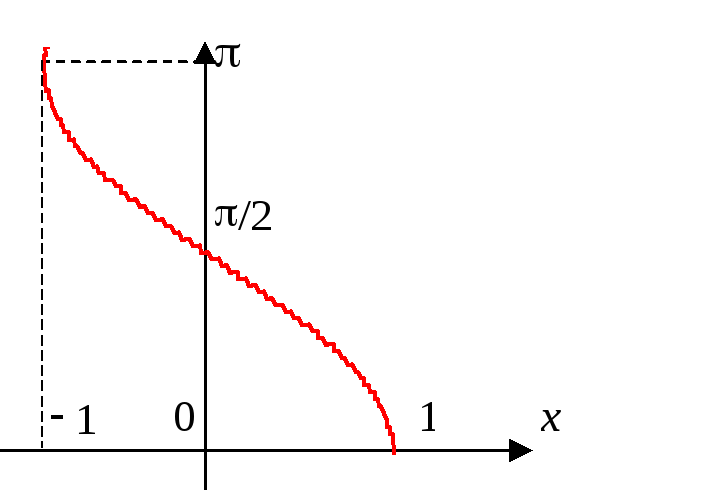
График
арккосинуса
Рис. 16 |
|
График
арктангенса
Р |
График
арккотангенса
Р |

 ;
; ;
; .
.








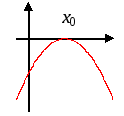
 Рис.
9
Рис.
9 Рис.
10
Рис.
10


 Рис.
14
Рис.
14
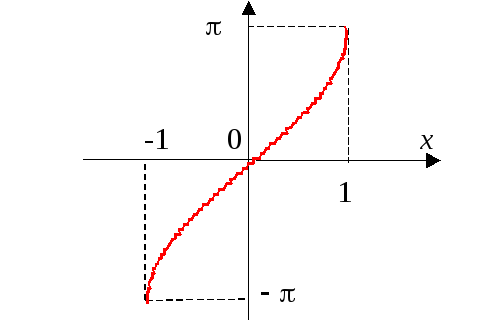
 ис.
17
ис.
17 ис.
18
ис.
18