
- •Оглавление
- •Предисловие
- •1. Множества. Числa. Действия над числами Множества. Операции над множествами
- •A и b - граничные точки конечного интервалаТабл. 6
- •Сокращение и расширение дроби:
- •Разделение отрезка длиной а на два отрезка х и а – х называется золотым сечением, если х – среднее геометрическое между а и а – х: ;
- •2. Степени, корни, многочлены
- •Операции со степенями и их свойства Табл. 12
- •Операции с корнями и их свойстваТабл. 13
- •3. Последовательности и суммы
- •4. Логарифмирование
- •Десятичные и натуральные логарифмы
- •5. Уравнения
- •6. Неравенства
- •7. Тригонометрия
- •2) ; 3) .
- •Приведение обратных тригонометрических функций:
- •Простейшие тригонометрические уравнения и их решение
- •8. Функции
- •9. Планиметрия
- •Подобия в прямоугольном треугольнике: ;;
- •С Рис. 39войства трапеции:
- •10. Стереометрия
- •Правильные многогранники
Десятичные и натуральные логарифмы
|
Десятичные логарифмы (основание a = 10): |
|
|
Натуральные логарифмы (основание a = e = 2,71828…): |
|
|
Соотношения между десятичными и натуральными логарифмами: |
|
5. Уравнения
Уравнение – равенство, содержащее одну или несколько неизвестных.
Решение (корень) уравнения – значение неизвестной, при которой уравнение превращается в верное числовое равенство.
Линейное уравнение
Общий
вид:
![]() .
Корень (решение)
.
Корень (решение)![]() .
.
Квадратное уравнение
Общий
вид: ![]() ;a
0.
;a
0.
Приведенное
квадратное уравнение: ![]() .
.
Неполные квадратные уравнения:
![]() ;
; ![]() ;
;![]() .
.
|
Дискриминант квадратного уравнения: |
|
Корни квадратного уравнения Табл. 18
|
Вид уравнения |
Дискриминант |
Корни |
|
Общий вид |
D > 0 |
Два различных корня
|
|
D = 0 |
Один
двукратный корень
| |
|
D < 0 |
Нет действительных корней. | |
|
Приведенное уравнение |
D* > 0 |
Два различных корня
|
|
D* = 0 |
Один
двукратный корень
| |
|
D* < 0 |
Нет действительных корней. |
Корни неполных квадратных уравнений Табл. 19
|
Вид уравнения |
Корни |
|
ax2 + c = 0 |
При
|
|
ax2 + bx = 0 |
|
|
ax2 = 0 |
|
Разложение квадратного трехчлена на множители Табл. 20
|
Случай |
Дискриминант |
Формула |
|
Общий случай |
|
|
|
|
| |
|
|
не раскладывается | |
|
Приведенный случай |
|
|
|
|
| |
|
|
не раскладывается |
Теорема Виета
|
для полного квадратного уравнения: |
x1
+ x2
=
|
|
для приведенного квадратного уравнения: |
x1 + x2 = p, x1 x2 = q. |
Биквадратное уравнение
Общий
вид:
![]() ,
a
0.
,
a
0.
Корни уравнения:
 ;
;
 ,
где
,
где![]() - дискриминант
- дискриминант
Приведенное кубическое уравнение
Общий
вид:
![]()
Корни уравнения (формула Кардано):
|
|
Система двух линейных уравнений с двумя неизвестными
|
Общий вид: |
|
где x и y - неизвестные, a1, b1, a2, b2 – коэффициенты при неизвестных |
Решение системы:
|
|
Иррациональные уравнения
|
Иррациональное уравнение – уравнение, содержащее неизвестное под знаком корня. |
Уравнение с нечетным показателем корня:
![]() равносильно уравнению:
равносильно уравнению:![]() ,
,![]() .
.
Уравнение с четным показателем корня:
![]() равносильно
уравнению
равносильно
уравнению
![]() при условии
при условии .
.
Устранение иррациональности в знаменателе при решении уравнений и преобразовании выражений:
|
|
|
Показательные уравнения
|
Показательное уравнение – уравнение, содержащее неизвестное в показателе степени. |
Уравнение
![]() (при
(при
![]() )
)
равносильно
уравнению
![]() .
.
Уравнение
![]() равносильно уравнению
равносильно уравнению![]()
при условии
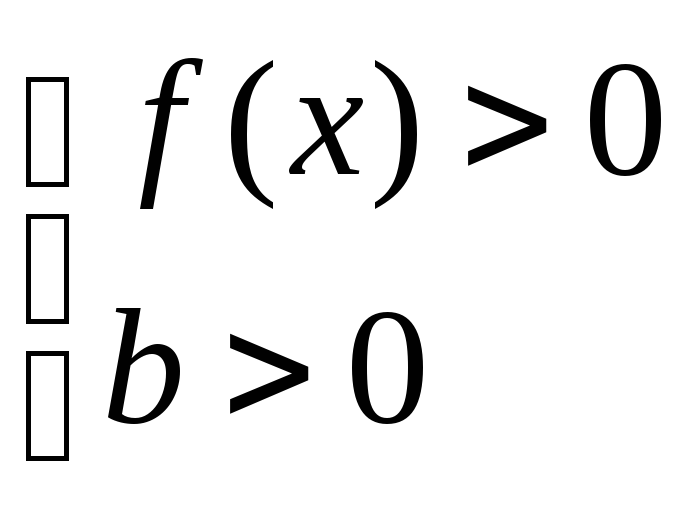 для любого числаа
(
для любого числаа
(![]() ).
).
Логарифмические уравнения
|
Логарифмическое уравнение – уравнение, содержащее неизвестное под знаком логарифма или в основании логарифма. |
Уравнение
![]() (при
(при![]() )
)
равносильно
уравнению
![]() при условии
при условии
 .
.
Уравнение
![]()
равносильно
уравнению
![]() при условии
при условии

 ;
;
 .
. ,
, .
При
.
При ,
где
,
где
 - дискриминант
- дискриминант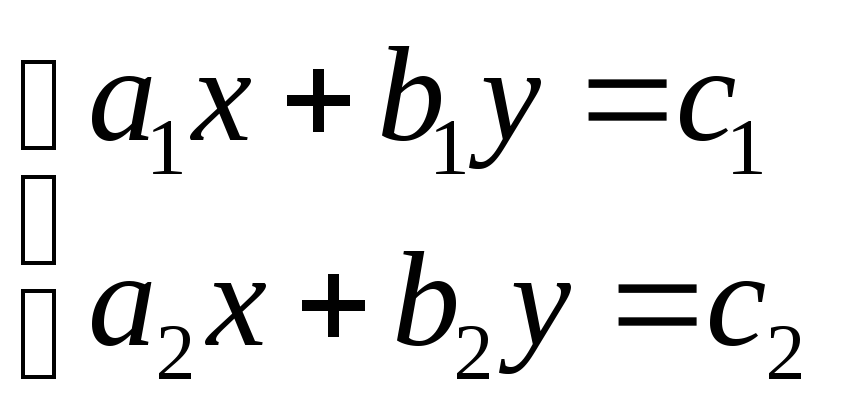
 ,
,
 ,
при
a1b2
a2b1
0.
,
при
a1b2
a2b1
0.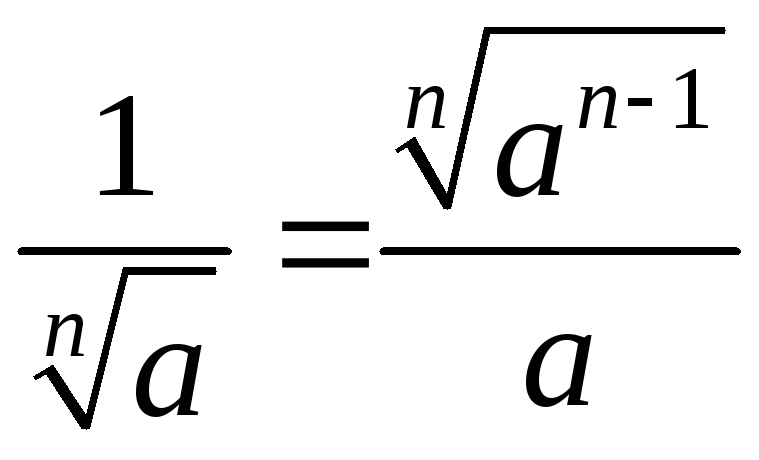 ;
; .
.