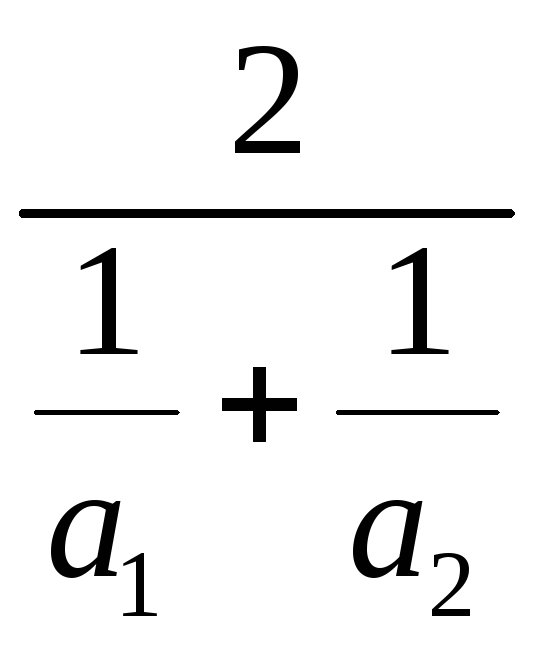Сокращение и расширение дроби:

Сокращение:

Расширение: ,k  0

Сложение и вычитание дробей:

с одинаковыми знаменателями:

;

с разными знаменателями:

.

Умножение и деление дробей:

Умножение	дроби на дробь:	;
	дроби на число:	;
Деление	дроби на дробь:	;
	числа на дробь:	;
	дроби на число:	.

Примечание. После умножения и деления дробь целесообразно сократить.

Пропорции и пропорциональности

Пропорция есть равенство двух отношений:
, где a, d - крайние члены, b, c - средние члены пропорции

Основное свойство пропорции:

.

Нахождение членов пропорции:

;

;

;

.

Другие свойства пропорции:

;

;

;

;

;

.

Представление пропорциональностей.

Прямая пропорциональность (прямая пропорциональная зависимость):	или .
Обратная пропорциональность (обратная пропорциональная зависимость):	или ;
где с – коэффициент пропорциональности

Средние значения Табл. 11

Наименование среднего	для двух чисел	для nчисел
Среднее арифметическое
Среднее геометрическое
Среднее гармоническое

Золотое сечение

Разделение отрезка длиной а на два отрезка х и а – х называется золотым сечением, если х – среднее геометрическое между а и а – х: ;

;;

2. Степени, корни, многочлены

Возведение в степень

Обозначение: , гдеb - основание степени,

n - показатель степени,

c - значение степени,

- степень.

Частные случаи.

Возведение в квадрат:	.	Возведение в степень нуля:		0n = 0.
Возведение в куб:	.	Возведение в степень единицы:		1n = 1.
Возведение в нулевую степень:			a0 = 1, a  0.

Операции со степенями и их свойства Табл. 12

Наименование	Формула
Умножение степеней с одинаковыми показателями (степень произведения)
Деление степеней с одинаковыми показателями (степень частного )
Умножение степеней с одинаковыми основаниями
Деление степеней с одинаковыми основаниями
Возведение степени в степень
Возведение в отрицательную степень

Извлечение корня

Обозначение: , где - знак корня,

a - подкоренное выражение,

n - показатель корня,

b - значение корня,

- корень степениn из числа a.

Равносильное равенство: .

Частные случаи

Квадратный корень из числа а: .

Кубический корень из числа а: .

Операции с корнями и их свойстваТабл. 13

Наименование	Формула
Корень как степень с дробным показателем
Умножение корней с одинаковыми показателями (корень из произведения)
Деление корней с одинаковыми показателями (корень из частного)
Возведение корня в степень
Извлечение корня из корня
Корни с четным показателем	, n  N
Деление корней с разными показателями и с разными подкоренными числами
Корни с нечетным показателем	, n  N
Умножение корней с разными показателями и с разными подкоренными числами
Корень из степени как степень с дробным показателем

Многочлены

Многочлен по одной переменной – алгебраическое выражение вида

,

где - коэффициенты многочлена (),х – переменная.

Степень многочлена . Корень многочлена, если.

Многочлен есть алгебраическая сумма одночленов: .

Разложение многочлена на множители:

,

где - корни многочлена (возможно, комплексные).

Разложение многочлена с действительными коэффициентами на линейные и неприводимые квадратные множители с действительными коэффициентами:

,

где - кратность корня;- кратность квадратного множителя;.

Дробно-рациональная функция (рациональная дробь) есть отношение многочленов

.

Рациональная дробь -правильная, если .

Представление рациональной дроби в виде суммы многочлена (целой части) и правильной дроби (остатка) :

.

Типы простейших дробей Табл. 14

I тип	II тип	III тип	IV тип

Здесь , - неприводимый квадратный трёхчлен.

Разложение правильной дроби со знаменателем в сумму простейших дробей:

,

где - действительные коэффициенты.