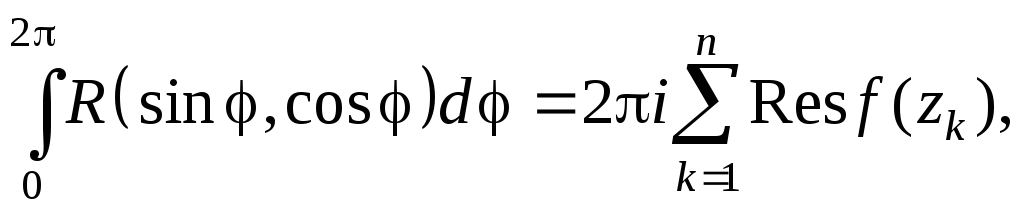Вычисление вычетов Табл. 97
|
Тип точки zo |
Формула для вычета |
|
Устранимая особая точка |
|
|
Простой полюс (полюс первого порядка) функции
|
а)
б)
|
|
Полюс порядка n |
|
|
Существенно особая точка |
(коэффициент ряда Лорана функции f(z) в окрестности точки zo) |
0
Вычисление интегралов с помощью вычетов Табл. 98
|
Наименование |
Формула |
|
Основная теорема Коши о вычетах |
|
|
|
|
|
Интеграл от рациональной функции от тригонометрических функций |
где
zk
- особые точки функции F(z)
в области |z|<1,
|
|
Несобственный интеграл |
где
zk
- особые точки функции f(z)
в верхней полуплоскости;
|
Интеграл
по замкнутому контуру ( f(z)
- аналитическая внутри контура) 
23. Теория вероятностей
Случайные события
Основные соединения Табл. 99
|
Определение |
Число соединений |
Пример. Даны три элемента: 1, 2, 3. |
|
Перестановка – - упорядоченное множество из данных n элементов |
Число перестановок из n элементов: Pn=n! |
Число перестановок из трех элементов P3=3!=6. Перестановки из трех элементов: 123, 132, 213, 231, 312, 321. |
|
Сочетание – - неупорядоченное подмножество, содержащее m элементов из данных n элементов |
Число сочетаний из n элементов по m:
|
Число
сочетаний из трех элементов по два
Сочетания из трех элементов по два: 12, 13, 23. |
|
Размещение – - упорядоченное подмножество, содержащее m элементов из данных n элементов |
Число размещений из n элементов по m:
|
Число
размещений из трех элементов по два:
Размещения из трех элементов по два: 12, 21, 13, 31, 23, 32. |
.
.Свойства комбинаторных формул
-
свойство симметрии
,
- рекуррентное соотношение
Сочетание с повторениями – неупорядоченная выборка m элементов из данных n элементов с возвращением.
Число
сочетаний с повторениями:
.
Размещение с повторениями – упорядоченная выборка m элементов из данных n элементов с возвращением.
Число
размещений с повторениями:
.
Случайные события
Обозначения: Ω – множество всех элементарных исходов опыта (испытания).
Невозможное событие: Ø. Достоверное событие: Ω.
Алгебраические операции над событиями Табл. 100
|
Наименование операции |
Обозна-чение |
Определение |
|
Сумма (объединение) двух событий |
A+B |
Событие, состоящее в том, что произошло или A, или B, или оба вместе. |
|
Произведение (совмещение) двух событий |
A·B |
Событие, состоящее в том, что произошли A и B вместе. |
|
Отрицание события A (противоположное для A) |
|
Событие, состоящее в том, что A не произошло. |
Свойства
операций:
;
;
;
.
Формулы
де Моргана:
; 
.
Несовместность
событий:
события A
и B
несовместны, если
.
Вероятность события A – числовая функция, определенная на множестве всех событий; обозначение: p(A).
|
Аксиомы вероятности: |
1.
2.
3.
|
;
;
для несовместных событий.
|
Формула классической вероятности (Ω – конечное множество): |
n – общее число всех элементарных (равновозможных) исходов, m – число элементарных исходов, благоприятствующих для события A. |
,