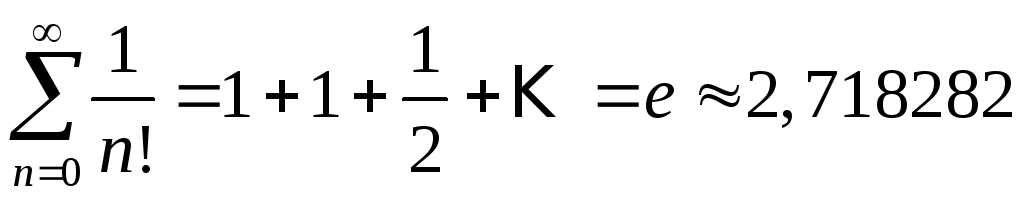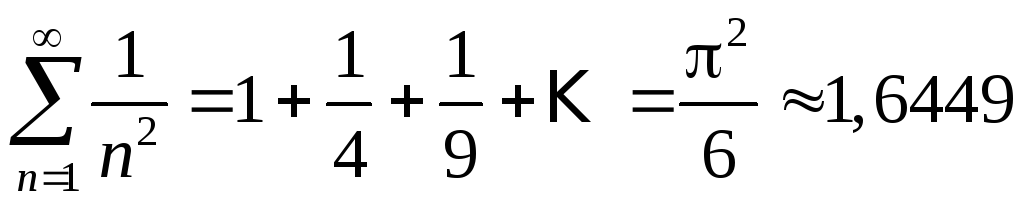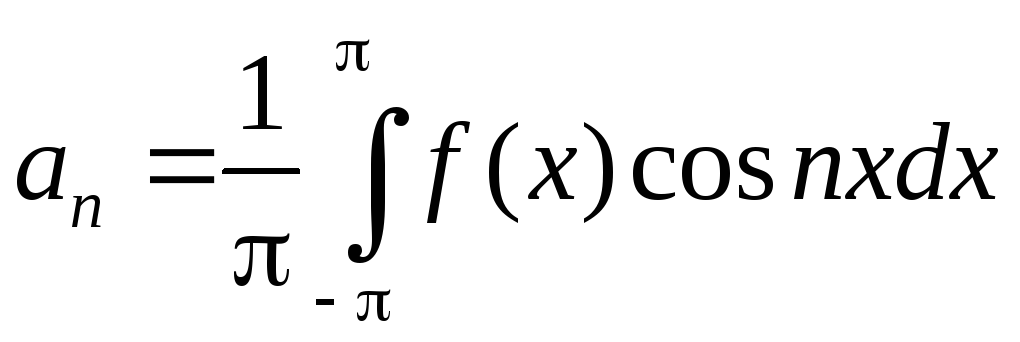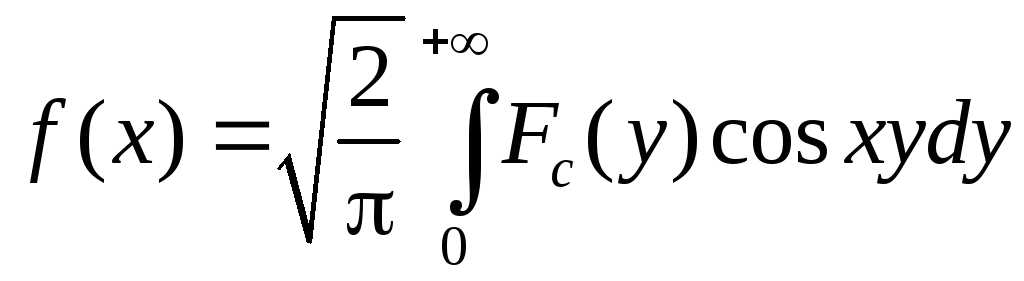17. Ряды Числовые ряды
Обозначение
числового ряда:
.
Частичная
сумма ряда: 
.
Сумма ряда:
.
Сходимость числового ряда
|
Необходимый признак сходимости: |
| |
|
Достаточные
признаки сходимости для ряда
| ||
|
Признак Даламбера |
|
при
при
|
|
Признак Коши (радикальный) |
|
при
при
|
|
Интегральный признак Коши |
ряд
сходятся или расходятся одновременно | |
|
Достаточный
признак сходимости для ряда
| ||
|
Признак Лейбница |
ряд
сходится, если 1)
2)
| |
,
где
,
ряд сходится,
ряд
расходится
,
ряд сходится,
ряд расходится
и
интеграл
, где
,
где
и
.
При этом
,
.
|
Абсолютная сходимость: |
ряд
|
|
Условная сходимость: |
ряд
|
|
Гармонический ряд |
|
|
Ряд Лейбница |
|
- сходится; ряд
- сходится.
- сходится; ряд
- расходится.
-
расходится 
-
сходится условно
Постоянная
Эйлера
Суммы некоторых числовых рядов
|
1. |
|
|
6. |
| ||
|
2. |
|
|
7. |
| ||
|
3. |
|
|
8. |
| ||
|
4. |
|
|
9. |
| ||
|
5. |
|
|
10. |
| ||
Степенные ряды
Определение степенного ряда:
.
Радиус сходимости степенного ряда
|
Формула Даламбера |
Формула Коши |
|
|
|
Ряд Тейлора (разложение функции в степенной ряд):
Ряд
Маклорена (
):
.
Формула
Стирлинга:
,
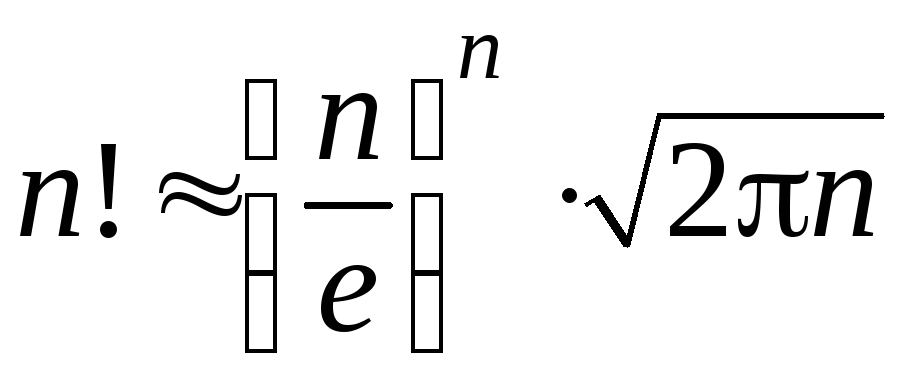гдеn
– достаточно большое число.
Разложения в степенной ряд элементарных функций Табл. 72
|
Функция |
Формула |
Область сходимости |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
при
при
при
Ряды Фурье
Условия
Дирихле сходимости
ряда Фурье к функции
:
функция
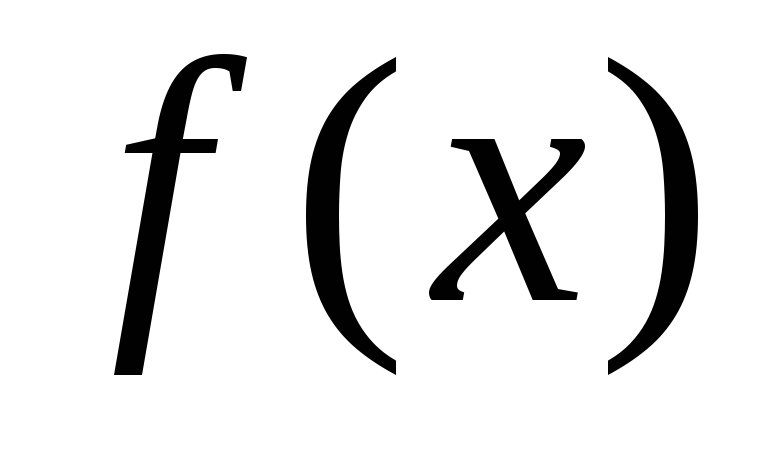непрерывна и монотонна на конечном
числе интервалов периода
;функция
имеет конечное число точек разрыва I
рода на интервале
.
Ряды Фурье для периодической функции Табл. 73
|
Период |
Разложение |
Коэффициенты |
|
|
|
|
|
| ||
|
| ||
|
|
|
|
|
| ||
|
|
Неполные ряды Фурье Табл. 74
|
Период |
Разложение |
Коэффициенты |
|
Для четной функции | ||
|
|
|
|
|
|
|
|
|
Для нечетной функции | ||
|
|
|
|
|
|
|
|
Ряд Фурье в комплексной форме Табл. 75
|
Период |
Разложение |
Коэффициенты |
|
|
|
|
|
|
|
|
Таблица некоторых разложений в ряд Фурье Табл. 76
|
Функция |
График |
Ряд Фурье |
|
|
|
|
|
|
|
|
|
|
| |
|
|
| |
Интеграл Фурье и преобразование Фурье
Интеграл Фурье (для функции, удовлетворяющей условиям Дирихле):
.
|
Косинус-преобразование Фурье |
Обратное преобразование |
|
|
|
|
Синус преобразование Фурье |
Обратное преобразование |
|
|
|
