- •Линейная алгебра
- •Матрицы
- •Векторная алгебра
- •13. Аналитическая геометрия Преобразование координат Преобразование координат на плоскости
- •Прямые линии и плоскости
- •Взаимное расположение двух прямых на плоскости Табл. 40
- •Р Рис. 50асстояние от точки до плоскости
- •14. Введение в анализ
- •Непрерывность функции
- •15. Дифференциальное исчисление Определение производной
- •Основные правила дифференцированияТабл. 51
- •Обратные гиперболические функции Табл. 54
- •Исследование функций
- •16. Интегральное исчисление Неопределенный интеграл
- •Свойства неопределенного интеграла Табл. 64
- •Основные методы интегрирования Табл. 65
- •Свойства определенного интеграла Табл. 69
Прямые линии и плоскости
Прямая на плоскости. Виды уравнений Табл. 39
|
№ |
Уравнение |
Наименование |
Параметры |
|
1 |
|
общее уравнение прямой на плоскости |
точек на прямой;
k - угловой коэффициент прямой;
a - отрезок, отсекаемый прямой на оси х;
b - отрезок, отсекаемый прямой на оси y;
t - параметр |
|
2 |
|
уравнение прямой, проходящей через данную точку | |
|
3 |
|
уравнение прямой с данным угловым коэффициентом | |
|
4 |
|
уравнение прямой, проходящей через данную точку с данным угловым коэффициентом | |
|
5 |
|
уравнение прямой, проходящей через две точки | |
|
6 |
|
уравнение прямой в отрезках | |
|
7 |
|
каноническое уравнение прямой | |
|
8 |
|
нормальное уравнение прямой | |
|
9 |
|
параметрические уравнения |

Расстояние от
точки
![]() до прямой
до прямой![]()
 .
.
Взаимное расположение двух прямых на плоскости Табл. 40
|
Название |
Формулы |
Обозначения |
|
Угол между прямыми |
|
прямых;
прямых;
|
|
Условие параллельности |
| |
|
Условие перпендикулярности |
n1 n2 n1n2 = 0 или A1A2 + B1B2 = 0; q1 q2 q1q2 = 0 или l1l2 + m1m2 = 0;
|
Плоскость в пространстве. Виды уравнений Табл. 41
|
№ |
Уравнение |
Наименование |
Параметры |
|
1 |
|
общее уравнение плоскости в пространстве |
- нормальный вектор плоскости;
a,b,c – отрезки, отсекаемые плоскостью на осях координат;
- направляющие косинусы нормального вектора плоскости; p - длина перпендикуляра, опущенного из начала координат на плоскость |
|
2 |
|
уравнение плоскости, проходящей через три точки | |
|
3 |
|
уравнение плоскости в отрезках | |
|
4 |
|
нормальное уравнение плоскости |
Р Рис. 50асстояние от точки до плоскости
 .
.
Взаимное расположение двух плоскостей в пространстве Табл. 42
|
Название |
Формулы |
Обозначения |
|
Угол между плоскостями |
|
плоскостей |
|
Условие параллельности |
| |
|
Условие перпендикулярности |
n1
n2
n1n2
= 0 или
|
Прямая в пространстве. Виды уравнений Табл. 43
|
№ |
Уравнение |
Наименование |
Параметры |
|
1 |
|
общие уравнения прямой в пространстве |
- направляющий вектор прямой;
- координаты фиксированных точек на прямой |
|
2 |
|
канонические уравнения прямой в пространстве | |
|
3 |
|
параметрические уравнения прямой в пространстве | |
|
4 |
|
уравнения прямой, проходящей через две фиксированные точки |

Взаимное расположение двух прямых в пространстве Табл. 44
|
Название |
Формулы |
Обозначения |
|
Угол между двумя прямыми |
cos= |
q1 = (l1, m1, n1) и q2 = (l2, m2, n2) - направляющие векторы прямых |
|
Условие параллельности |
q1
||
q2
| |
|
Условие ортогональности |
q1 q2 q1q2 = 0 или l1l2 + m1m2 + n1n2 = 0 |
Взаимное расположение прямой и плоскости Табл. 45
|
Название |
Формулы |
Обозначения | ||
|
Угол между прямой и плоскостью |
|
q = (l, m, n) - направляющий вектор прямой;
(xo, yo, zo) - точка на прямой;
n = (A, B, C) - нормальный вектор плоскости | ||
|
Условие параллельности |
n q nq = 0 или Al + Bm + Cn = 0 | |||
|
а) прямая не лежит в плоскости |
Axo+ Byo+ Czo 0 | |||
|
б) прямая лежит в плоскости |
Axo+ Byo+ Czo = 0 | |||
|
Условие пересечения прямой и плоскости |
nq 0 или Al + Bm + Cn 0 | |||
|
Условие перпендикулярности прямой и плоскости |
n
||
q
| |||
Кривые второго порядка
Окружность
|
Каноническое
уравнение:
Радиус окружности: a. |
| |||
|
Параметрические уравнения: |
|
Уравнение в полярных координатах: |
| |
|
Уравнение
окружности радиуса
в
точке с координатами
| ||||
Эллипс
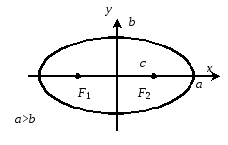
|
Каноническое уравнение:
Полуоси
эллипса:
Фокусное
расстояние: c.
Фокусы:
Уравнения
директрис:
|
Рис. 53 | |||
|
Параметрическое уравнение: |
|
Уравнение в полярных координатах: |
| |
Парабола
|
Каноническое уравнение:
Параметр: p.
Фокус:
Уравнение
директрисы:
|
| |
|
Уравнение в полярных координатах: |
| |
Гипербола
|
Каноническое уравнение:
Действительная полуось: a, мнимая полуось: b. Фокусное расстояние: с. Фокусы:
Уравнения
асимптот:
Эксцентриситет:
Уравнения
директрис:
|
|
| |
|
|
| ||
|
Параметрические
уравнения: | |||
|
Уравнение в
полярных координатах:
|
| ||
Классификация кривых второго порядка
Общее алгебраическое уравнение кривой второго порядка:
![]() .
.
Инварианты уравнения относительно преобразований декартовой системы координат:
![]() ;
;
![]() ;
; .
.
Классификация
линий при
![]() Табл.
46
Табл.
46
|
Знак
|
Тип линии |
Знак
|
Линия |
|
|
эллиптический |
|
эллипс |
|
|
точка | ||
|
|
мнимый эллипс | ||
|
|
гиперболический |
|
гипербола |
|
|
пара пересекающихся прямых | ||
|
|
параболический |
|
парабола |
|
|
пара действительных либо мнимых параллельных прямых |
Поверхности второго порядка Табл.47
|
Каноническое уравнение |
Наименование |
Параметры |
Чертеж |
|
|
сфера |
a – радиус |
|
|
|
эллипсоид |
|
|
|
|
однополостный гиперболоид |
|
|
|
|
двуполостный гиперболоид |
|
|
|
|
эллиптический параболоид |
|
|
Табл. 47 (продолжение)
|
|
гиперболический параболоид |
|
|
|
|
конус |
|
|
|
|
параболический цилиндр |
р - параметр |
|
|
|
эллиптический цилиндр |
|
|
|
|
гиперболический цилиндр |
|
|

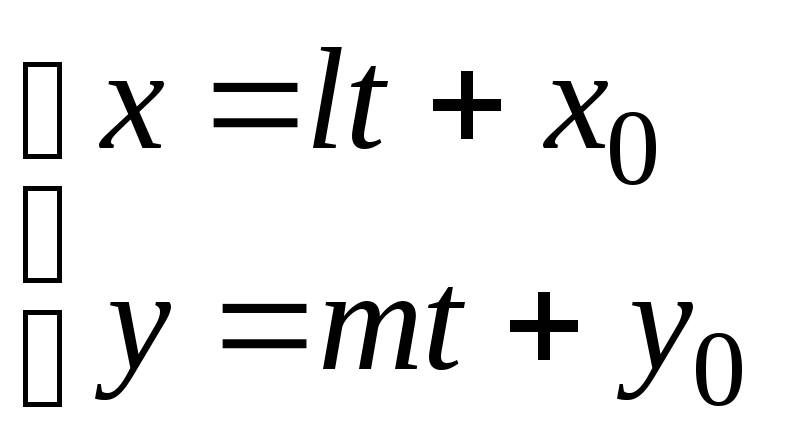
 ;
;
 ;
;







 Рис.
52
Рис.
52
 .
.
 .
. ;
; Рис.
54
Рис.
54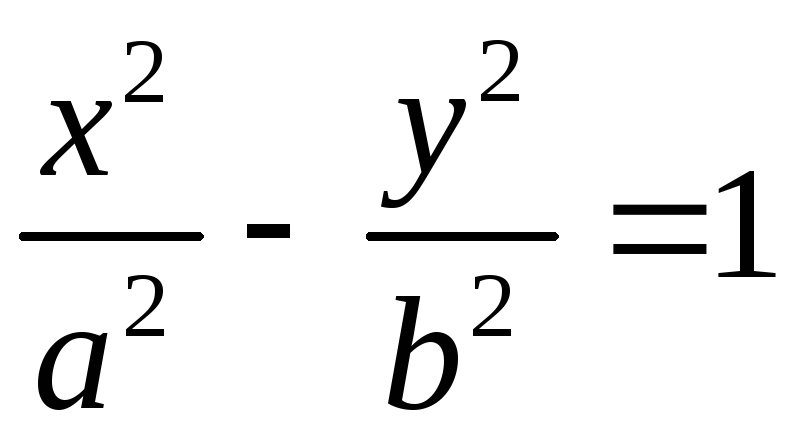 .
. Рис.
55
Рис.
55