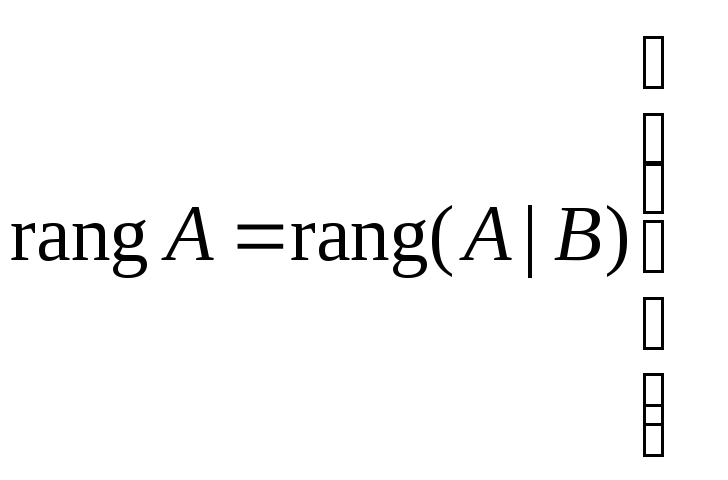Линейная алгебра
Определители (детерминанты)
Обозначения
определителя матрицы А:,detA,
.
|
Определитель второго порядка:. |
|
|
|
Определитель третьего порядка: |
|
|
Определитель порядка n
|
Разложение определителя n-го порядка по i-й строке: |
Разложение определителя n-го порядка по j-ому столбцу: |
|
|
|
|
определителя вычёркиванием i-й строки и j-го столбца. | |
- алгебраическое
дополнение элемента
,
,
-
минор элемента
,
т.е. определитель, получаемый из
исходногоМатрицы
|
(n строк и m столбцов): |
|
Матрица
размерами nm
,
;
.Равенство
матриц:
,
если эти матрицы одного размера и
.
Квадратная
матрица порядка n:
.
Невырожденная
(неособая) квадратная матрица А:
.
Подматрица матрицы A: матрица, полученная вычеркиванием части строк
и (или) столбцов матрицы A.
Минор матрицы A – определитель квадратной подматрицы матрицы A.
Ранг матрицы
-
наибольший порядок её ненулевого минора
или
наибольшее число линейно независимых строк (столбцов) матрицы А.
Операции над матрицами Табл. 37
|
Название |
Формула |
Свойства | |
|
Сложение матриц |
|
- ассоциативность:
-
коммутативность:
| |
|
Пример (для квадратных матриц второго порядка):
| |||
|
Умножение матрицы на число |
|
- дистрибутивность:
| |
|
Пример (для квадратной матрицы второго порядка):
| |||
|
Умножение матриц |
|
- ассоциативность:
- дистрибутивность
(для квадратных матриц) | |
|
Пример (для квадратных матриц второго порядка):
| |||
|
Транспонирование матрицы |
|
| |
|
Пример (для квадратной матрицы второго порядка):
| |||
|
Обращениематрицы |
|
| |
|
Пример (для квадратной матрицы второго порядка):
| |||
,
;
;
;
,
;
- обратная матрица
для
;
,
,
где
-алгебраическое
дополнение элемента
;
;
Некоторые виды матриц
|
нулевая матрица: |
|
матрица-строка:
|
матрица-столбец: |
|
Некоторые виды квадратных матриц
-
единичная матрица:
диагональная матрица:
для всех
треугольная матрица:
для всех
,
либо для всех
,пример:
ортогональная матрица:
,пример:
Элементарные преобразования матрицы:
1) перестановка строк (столбцов);
умножение строки (столбца) на число, отличное от нуля;
прибавление к элементам строки (столбца) соответствующих элементов другой строки (столбца), предварительно умноженных на любое число.
Эквивалентность матриц
Матрицы А и В эквивалентны (обозначение: А ~ В ), если они переводятся друг в друга с помощью элементарных преобразований.
Всякая
матрица А
эквивалентна матрице вида
,
где число единиц равно рангу матрицыА.
Системы линейных уравнений
Система n линейных уравнений с m неизвестными
|
|
ai j –коэффициент в i-ом уравнении при j-ом неизвестном;
|
-
неизвестные;
-
свободные члены.Матричный
вид системы линейных уравнений: 
,
где
|
матрица системы |
столбец неизвестных, |
столбец свободных членов. |
-
-
-Исследование систем линейных уравнений
Расширенная
матрица системы
:
матрица системы А
с добавленным справа столбцом свободных
членов В.
|
|
|
система совместна и неопределенна; решение не единственно, число
свободных переменных
|
|
|
система совместна и определена; решение единственно | |
|
|
- система несовместна (не имеет решений) | |
Исследование однородной системы (B = О):
|
|
Однородная система всегда разрешима. Если
Если
|
,
то система имеет только нулевое
(тривиальное) решение
.
,
то имеются также и ненулевые решения.Решение систем n линейных уравнений с n неизвестными
|
Формулы Крамера |
|
|
- определитель
матрицы системы (
),
- определитель,
полученный при замене i-го
столбца матрицы системы A
на столбец свободных членов В.