Дискретная математика / ЛИТЕРАТУРА / Лекции по теории графов

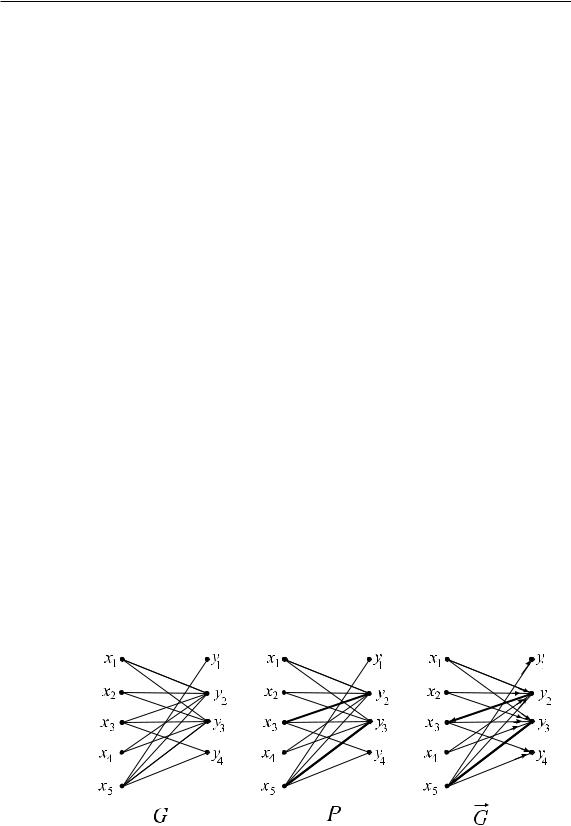
10.Задачи на двудольных графах

Решение. Построим данный граф (рис. 48). Выделим в нем некоторое максимальное паросочетание P :

XP = {x3, x5}, YP = {y2, y3}, P = {(x3, y2), (x5, y3)}.

−→ −→

Построим также орграф G(X, Y, E ) (ðèñ. 48).

Ðèñ. 48.

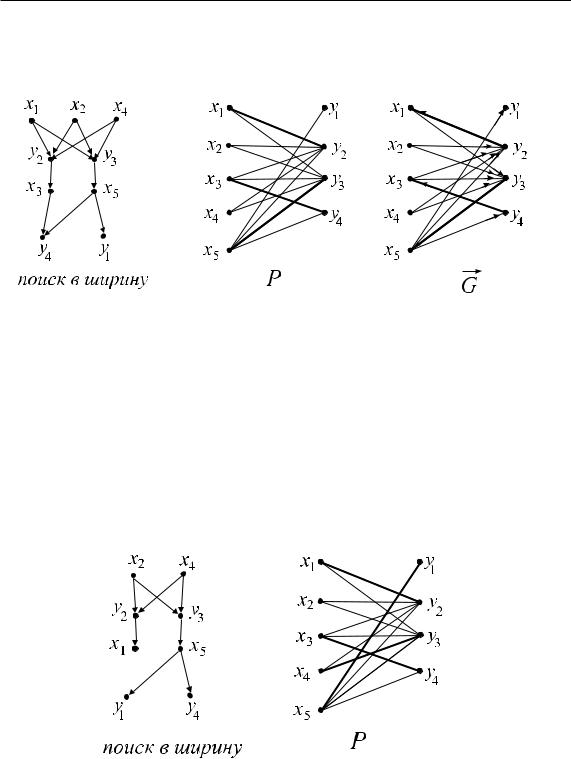
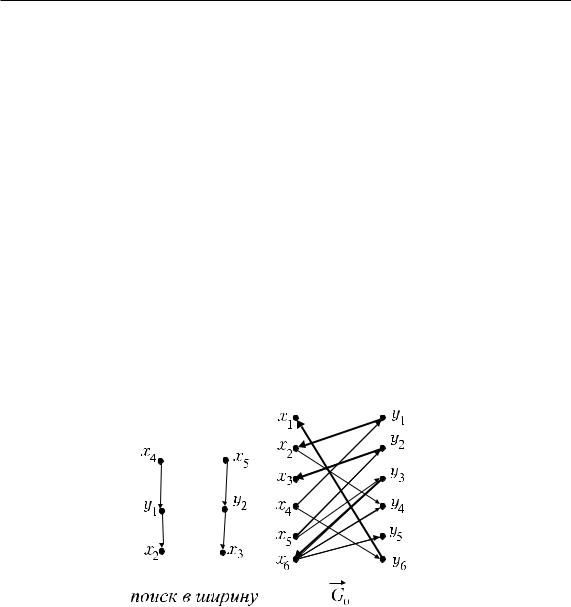
Выполним из множества вершин {x1, x2, x4} поиск в ширину (рис. 49). В результате поиска получит метку вершина y4: x1, y2, x3, y4. Â ïàðî- сочетание добавляем ребра (x1, y2), (x3, y4) и удаляем ребро (x3, y2)

71

10.Задачи на двудольных графах

(ðèñ. 49).

Ðèñ. 49.

XP = {x1, x3, x5}, YP = {y2, y3, y4}, P = {(x1, y2), (x3, y4), (x5, y3)}.

Выполним поиск в ширину из множества вершин {x2, x4}. В результате поиска получит метку вершина y1: x4, y3, x5, y1. В паросочетание добавляем ребра (x4, y3), (x5, y1) и удаляем ребро (x5, y3) (ðèñ. 50).

Ðèñ. 50.

XP = {x1, x3, x4, x5}, YP = {y1, y2, y3, y4},

P = {(x1, y2), (x3, y4), (x4, y3), (x5, y1)}.

Òàê êàê YP = Y , то алгоритм прекращает работу. P наибольшее паросочетание.

72

10.Задачи на двудольных графах

10.2.Алгоритм построения совершенного паросочетания минимального веса в двудольном нагруженном графе

Допустим имеется несколько работников и столько же "работ". Каждый работник может выполнять некоторые из работ и брать за них плату (по своему усмотрению). Как распределить всех работников таким образом, чтобы каждому достался один вид работ и суммарная плата была наименьшей? Сформулированная задача называется "задача о назначениях" и ее решение сводится к отысканию в двудольном нагруженном графе совершенного паросочетания минимального веса.

Пусть G(X, Y, E), ãäå |X| = |Y | = n полный двудольный взвешенный

граф, заданный матрицей весов WXY (G). Требуется найти в данном графе

паросочетание, вес которого минимален.

Для существования совершенного паросочетания в двудольном графе, необходимо, чтобы доли имели равное количество вершин (см. следствие 1 теоремы Холла). Полнота двудольного графа с долями равной мощности обеспечивает достаточное условие существования совершенного паросоче- тания (см. следствие 2 теоремы Холла). Алгоритм применим к любому двудольному графу (не обязательно полному), удовлетворяющему теореме Холла.

Так как для каждой вершины в совершенное паросочетание входит только одно инцидентное ей ребро, то решение задачи не изменится, если вес всех ребер инцидентных какой-либо вершине, увеличить (или уменьшить) на одно и то же число. Исходя из этого, можем считать, что веса всех ребер графа неотрицательны.

Если веса всех ребер графа неотрицательны и некоторое совершенное паросочетание состоит из ребер веса 0, то оно является решением задачи.

Перед началом работы алгоритма преобразуем матрицу весов графа (а значит, и сам граф): из каждой строки матрицы WXY (G) вычтем ми-

нимальный элемент этой строки, а затем каждого столбца вычтем минимальный элемент этого столбца. В преобразованном графе будет не менее n ребер веса 0.

Øàã 1. Строим граф G0(X, Y, E0), ãäå E0 множество ребер графа G, имеющих вес 0. Выделяем в графе G0 какое-либо максимальное паро- сочетание P . Пусть XP è YP множества вершин, инцидентных ребрам паросочетания P (XP X è YP Y ).

росочетание P , преобразуем в дуги, направленные из Y â X, à âñå

73

10.Задачи на двудольных графах

ребра, не входящие в паросочетание P , преобразуем в дуги, направленные из X â Y .

−→

Шаг 3. Применим к орграфу G0 поиск в ширину из множества вершин X \ XP . Если будет найден путь u, w1, w2, . . . , wk, v, такой, что

u X \ XP è v Y \ YP , то переходим к øàãó 4. Иначе переходим к øàãó 6.

−→

Шаг 4. Преобразуем орграф G0. Заменим каждую дугу найденного пути на обратную ей:

EP := (EP \{(w1,w2), (w3,w4), ..., (wk−1, wk)}) {(u,w1), (w2,w3),..., (wk,v)},

XP := XP {u}, YP := YP {v}.

При этом, в графе G0 будет найдено новое максимальное паросоче- тание P (из ребер, соответствующих дугам из YP {v} â XP {u}), мощность которого больше мощности предыдущего на 1.

Øàã 5. Åñëè X \ XP = Y \ YP = , то алгоритм заканчивает работу, Pискомое совершенное паросочетание. Иначе переходим к øàãó 3 .

−→

Øàã 6. Пусть X′ X, Y ′ Y подмножества вершин орграфа G0,

получивших метки в результате поиска в ширину (на шаге 3 ). Среди ребер (u, v) графа G таких, что u X′, v Y \ Y ′ ищем ребро

минимального веса (обозначим этот вес m).

Øàã 7. Преобразуем веса ребер исходного графа G следующим образом: из веса каждого ребра инцидентного вершине из множества X′ âû- ÷òåì m, а затем к весу каждого ребра, инцидентного вершине из множества Y ′, прибавим m (вес ребер инцидентных вершинам обоих множеств при этом не изменится останется равным 0).

−→ −→

Шаг 8. Преобразуем орграф G0(X, Y, E0). Добавим появившиеся в ре- зультате преобразования на øàãå 7 äóãè âåñà 0 èç X′ â Y \Y ′ и удалим

äóãè èç X \ X′ â Y ′, вес которых увеличился. Переходим к шагу 3 .

74

10.Задачи на двудольных графах

Пример 10.2. В двудольном графе, заданном матрицей весов, найти совершенное паросочетание минимального веса (проверить выполнение условий теоремы Холла).

Решение. Убедимся в том, что для любого подмножества вершин выполняется условие теоремы Холла: |A| ≤ | (A)|. Минимальная

степень вершины в графе равна 3. Следовательно, мощность окрестности любого подмножества вершин не менее 3. Следовательно, для одно-, двух- и трехэлементных подмножеств вершин условие теоремы выполнено.

 äîëå X вершина степени 3 одна, а в доле Y таких вершин две. Зна-

чит любое множество из четырех вершин содержит несколько вершин, степень которых больше трех (это верно для обоих долей). Следовательно, условие теоремы имеет место для четырехэлементных подмножеств вершин каждой доли.

Любое пятиэлементное подмножество множества X содержит вер- øèíû x5 èëè x6, а любое пятиэлементное подмножество множества Y содержит вершины y1 èëè y2 (перечисленные вершины имеют сте-

пень 5). Следовательно, для пятиэлементных подмножеств условие теоремы также выполняется.

Наконец, для самих множеств X è Y выполнение неравенства |A| ≤ | (A)| равносильно отсутствию изолированных вершин (если бы та-

кие вершины в графе были, то им соответствовали бы строки или столбцы, полностью состоящие из " ∞").

Преобразуем матрицу смежности графа так, как предлагается в алгоритме. А именно, вычтем из каждой строки, а затем из каждого столбца минимальный элемент:

75

10.Задачи на двудольных графах

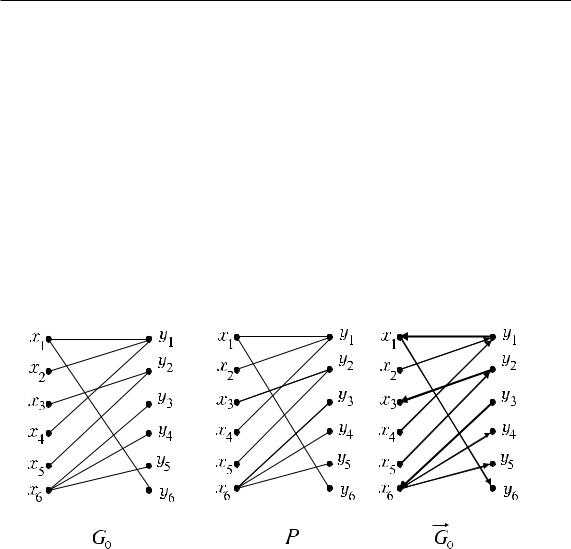
Построим граф G0(X, Y, E0) (ðèñ. 51), ãäå E0 множество ребер гра- фа c весом 0. Выделим в G0 некоторое максимальное паросочетание P (ðèñ. 51):

XP = {x1, x3, x6}, YP = {y1, y2, y3}, EP = {(x1, y1), (x3, y2), (x6, y3)}.

−→ −→

Построим также орграф G0(X, Y, E0) (рис. 51): все ребра, входящие в паросочетание P преобразуем в дуги, направленные из множества

Y в множество X, а все ребра, не входящие в паросочетание P преобразуем в дуги, направленные из множества X в множество Y .

Ðèñ. 51.

Òàê êàê X \ XP = {x2, x4, x5} ̸= è

−→

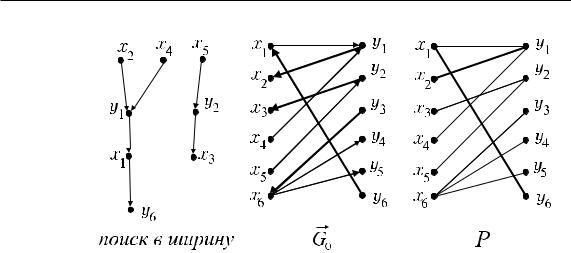
Y \ YP = {y4, y5, y6} ̸= , то в графе G0 из множества X \ XP выпол- няем поиск в ширину (рис. 52). Наша цель найти путь в вершины из доли Y , не инцидентные ребрам паросочетания P : y4, y5, y6. Â результате находим путь x2, y1, x1, y6 в вершину y6 Y \ YP . Â ïàðî- сочетание добавляем ребра (x2, y1), (x1, y6) и удаляем ребро (x1, y1) (ðèñ. 52):

XP = {x1, x2, x3, x6}, YP = {y1, y2, y3, y6},

EP = {(x2, y1), (x1, y6), (x3, y2), (x6, y3)}.

76

10.Задачи на двудольных графах

Ðèñ. 52.

Поиск в ширину из множества не инцидентных ребрам паросочетания вершин {x4, x5} во множество Y \ YP = {y4, y5} не дает результатов

(рис. 53). Следовательно, переходим к шестому шагу алгоритма. В результате поиска в ширину метки получили следующие вершины:

X′ = {x2, x3, x4, x5}, Y ′ = {y1, y2}.

Среди ребер (u, v) графа G таких, что

u X′, v Y \ Y ′ = {y3, y4, y5, y6}

(в приведенной ниже матрице они выделены жирным шрифтом) найдем ребро минимального веса. В данном случае это может быть ребро (x2, y4) веса 1. Преобразуем веса ребер графа G следующим образом:

из веса всех ребер инцидентных вершинам x2, x3, x4, x5

(из элементов соответствующих строк матрицы WXY (G) вычтем 1), а к весу всех ребер инцидентных вершинам y1, y2 прибавим 1 (к эле- ментам первого и второго столбцов матрицы WXY (G) прибавим 1).

77

10.Задачи на двудольных графах

В результате, вес ребер (x5, y3), (x5, y6) è (x2, y4) стал равен нулю,

(x2, y4) и удалим дугу (x1, y1) (ðèñ. 53).

Ðèñ. 53.

Òàê êàê X \ XP = {x4, x5} ≠ è Y \ YP = {y4, y5} ≠ , то в графе

−→

G0 из множества X \ XP выполняем поиск в ширину во множество

{y4, y5}(рис. 54). В результате найдем путь x4, y1, x2, y4 и получит метку вершина y4. В паросочетание добавляем ребра (x4, y1), (x2, y4) и удаляем ребро (x2, y1) (ðèñ. 54):

XP = {x1, x2, x3, x4, x6}, YP = {y1, y2, y3, y4, y6},

EP = {(x4, y1), (x2, y4), (x1, y6), (x3, y2), (x6, y3)}.

78

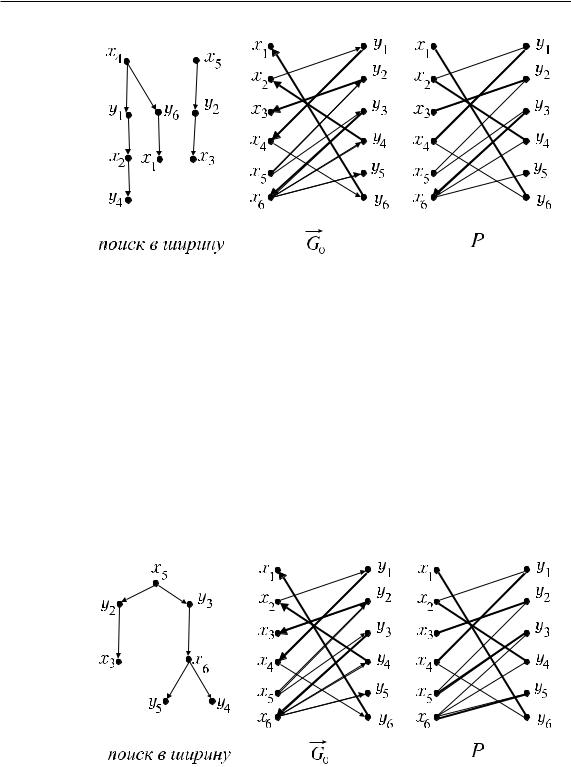
10.Задачи на двудольных графах

Ðèñ. 54.

−→

Òàê êàê X \ XP = {x5} ≠ è Y \ YP = {y5} ̸= , то в графе G0 èç вершины x5 выполняем поиск в ширину (рис. 55). В результате найдем путь x5, y3, x6, y5 и получит метку вершина y5. В паросочетание добавляем ребра (x5, y3), (x6, y5) и удаляем ребро (x6, y3) (ðèñ. 55):

P = {(x4, y1), (x2, y4), (x1, y6), (x3, y2), (x5, y3), (x6, y5)},

XP = {x1, x2, x3, x4, x5, x6} = X, YP = {y1, y2, y3, y4, y5, y6} = Y.

Ðèñ. 55.

Òàê êàê X \ XP = Y \ YP = , то алгоритм заканчивает работу. P искомое паросочетание. Вычислим его вес:

w(P ) = w16 + w24 + w32 + w41 + w53 + w65 = 1 + 3 + 3 + 4 + 6 + 6 = 23.

Пример 10.3. В полном двудольном графе, заданном матрицей длин дуг,

79

10.Задачи на двудольных графах

найти совершенное паросочетание минимального веса.

Решение. Преобразуем матрицу весов графа так, как предлагается в алгоритме. А именно, вычтем из каждой строки, а затем из каждого столбца их минимальный элемент:

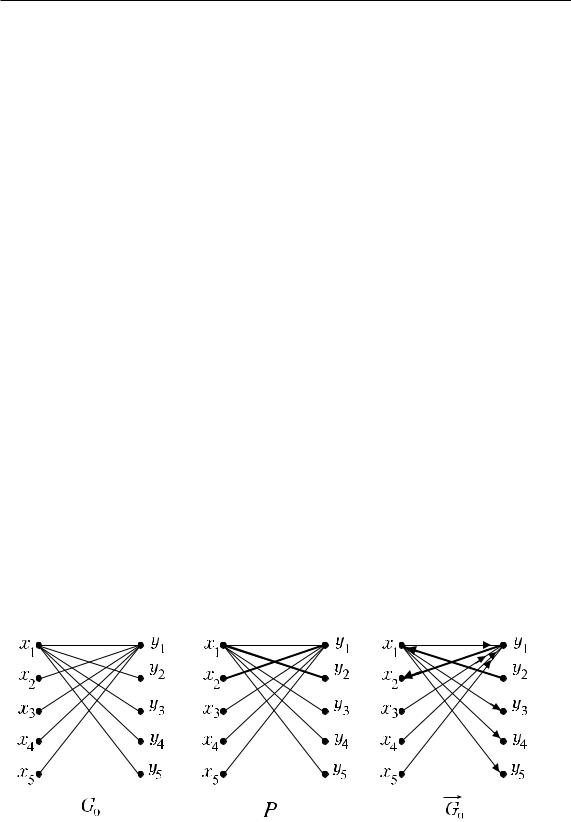
Построим граф G0(X, Y, E0) (ðèñ. 56), ãäå E0 множество ребер гра- фа c весом 0. Выделим в G0 некоторое максимальное паросочетание

P : XP = {x1, x2}, YP = {y1, y2}, P = {(x1, y2), (x2, y1)}.

−→ −→

Построим также орграф G0(X, Y, E0) (рис. 56): все ребра, входящие в паросочетание P , преобразуем в дуги, направленные из множества

Y в множество X, а все ребра, не входящие в паросочетание P преобразуем в дуги, направленные из множества X в множество Y .

Ðèñ. 56.

ширину во множество Y \ YP = {y3, y4, y5} (рис. 57). В результате ни

80