
Дискретная математика / ЛИТЕРАТУРА / Лекции по теории графов
.pdf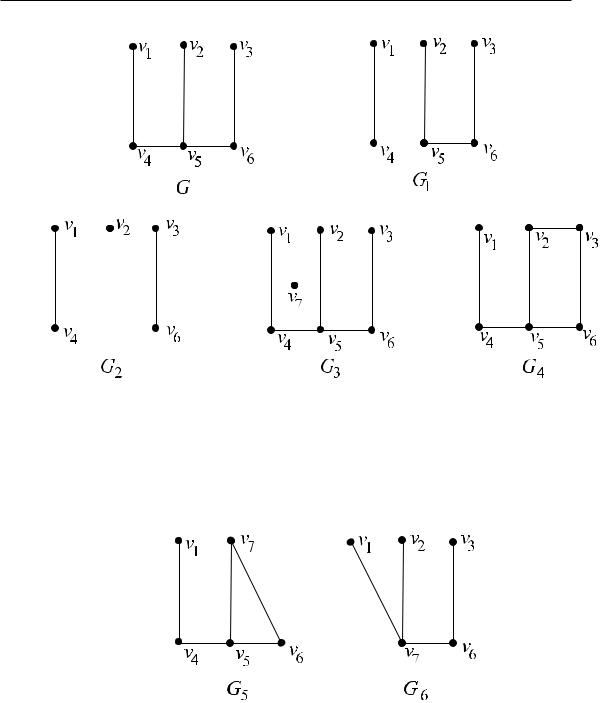
1.Графы и операции над ними
Ðèñ. 6.
На рис. 7 изображены графы, полученные применением к G операций отождествление вершин v2, v3 (ðèñ. 7, G5) и стягивание ребра (v4, v5) (ðèñ. 7, G6).
Ðèñ. 7.
Размножение вершины. При размножении вершины u графа G ïîëó- чаем новый граф G′ следующим образом: добавим новую вершину u′ и новое ребро (u, u′); добавим ребра (u′, vi), vi (u) (т.е. ребра, соединяющие новую вершину со всеми вершинами из окрестности u).
Расщепление вершины. При расщеплении вершины u графа G получа- ем новый граф G′ следующим образом: разобьем окрестность вершины u на два произвольных непересекающихся подмножества 1 è
11
1.Графы и операции над ними
2; удалим вершину u из графа; добавим новые вершины u1 è u2; добавим ребра (u1, vi), vi 1, (u2, wj), wj 2 è (u1, u2).
Дублирование вершины. При дублировании вершины u графа G полу- чаем новый граф G′ следующим образом: добавим вершину u′; äîáà- вим ребра (u′, vi), vi (u) (т.е. ребра, соединяющие новую вершину со всеми смежными с вершиной u).
Разбиение ребра. При разбиении ребра (u, v) графа G получаем новый граф G′ следующим образом: удалим ребро (u, v) из множества р¼бер графа; добавим новую вершину w; добавим р¼бра (u, w) è (w, v). В некоторых случаях используется обобщенное разбиение ребра (u, v)замена его на множество ребер {(u, u1), (u1, u2), ..., (un, v)}.
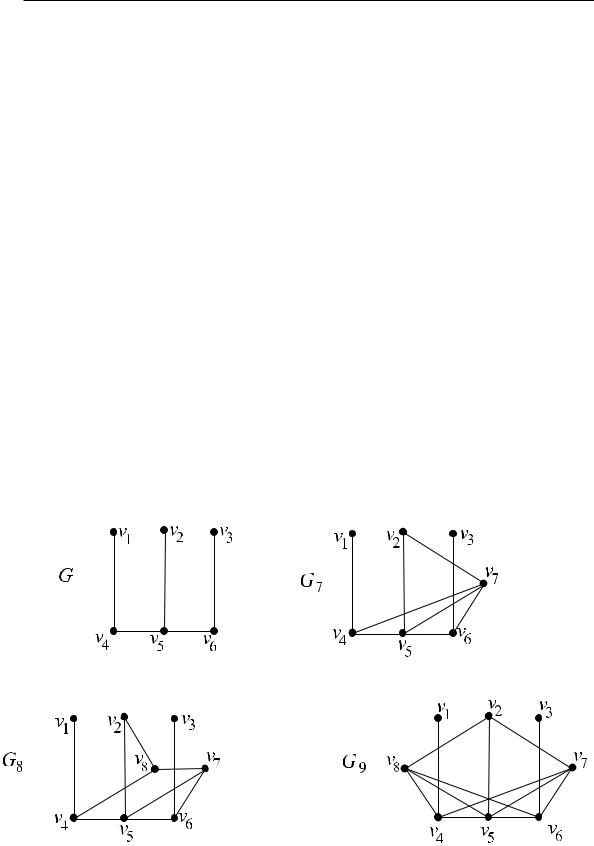
Пример 1.7. На рис. 8 продемонстрировано размножение вершины v5 графа G, расщепление вершины v7 графа G7, дублирование вершины v7 графа G7 (графы G7, G8 è G9
Ðèñ. 8.
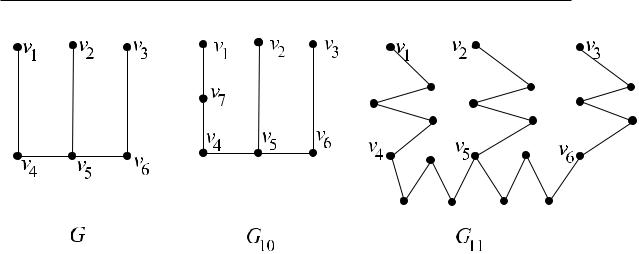
На рис. 9 изображены граф G; ãðàô G10, полученный из G разбиением ребра (v1, v4); ãðàô G11, полученный из G обобщенным разбиением всех ребер.
12
1.Графы и операции над ними
Ðèñ. 9.
Объединение графов. При объединении графов получаем граф, состоящий из всех вершин и ребер исходных графов:
G1(V1, E1) G2(V2, E2) = G(V1 V2, E1 E2).
Если множества вершин и ребер исходных графов не пересекались, то объединение называется дизъюнктным.
Замечание. Как правило, операция объединения применяется к нескольким (необязательно двум) частям одного и того же графа.
Пересечение графов. При пересечении графов получаем граф, множества вершин и р¼бер которого состоят из вершин и р¼бер, принадлежащих всем исходным графам:
G1(V1, E1) ∩ G2(V2, E2) = G(V1 ∩ V2, E1 ∩ E2).
Если множества вершин исходных графов не пересекались, то пересечение графов пусто. Непустым может быть пересечение некоторых частей одного и того же графа.
Соединение графов. При соединении графов получаем граф, который является результатом их объединения и добавления ребер, инцидентных вершинам из разных графов:
G1(V1, E1)+G2(V2, E2) = G(V1 V2, E1 E2{(v1, v2)| v1 V1, v2 V2})
(при условии, что V1 ∩ V2 = , E1 ∩ E2 = ).
13
1.Графы и операции над ними
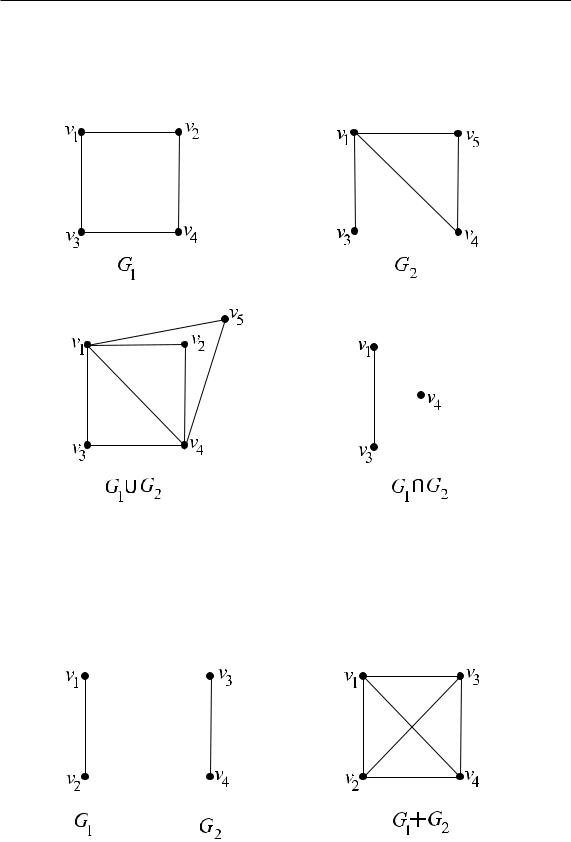
Пример 1.8. На рис. 10 изображены графы G1, G2, их объединение G1 G2 и пересечение G1 ∩ G2.
Ðèñ. 10.
Пример 1.9. На рис. 11 изображены графы G1, G2 è ãðàô G1 + G2, ïî- лученный в результате их соединения.
Ðèñ. 11.
Декартово произведение графов. Множество вершин произведения G1×
G2 графов G1(V1, E1) è G2(V2, E2) состоит из упорядоченных пар
14
1.Графы и операции над ними
(u1, u2), u1 G1, u2 G2:
V (G1 × G2) = V (G1) × V (G2).
Множество ребер декартова произведения графов определяется следующим образом: ((u, v1), (u, v2)) ребро в графе G1 × G2, åñëè v1, v2
смежны в графе G2 è ((u1, v), (u2, v)) ребро в графе G1 × G2, åñëè u1, u2 смежны в графе G1:
E(G1 × G2) = {((u, v1), (u, v2))|u V1, (v1, v2) E2}
{((u1, v), (u2, v))| v V2, (u1, u2) E1}
(при условии, что V1 ∩ V2 = , E1 ∩ E2 = ). Для того, чтобы изобразить декартово произведение графов G1 × G2 на рисунке, заме- ним каждую вершину графа G1 íà ãðàô G2 и размножим ребра, инцидентные двум различным копиям G2 так, чтобы они соединяли идентичные вершины.
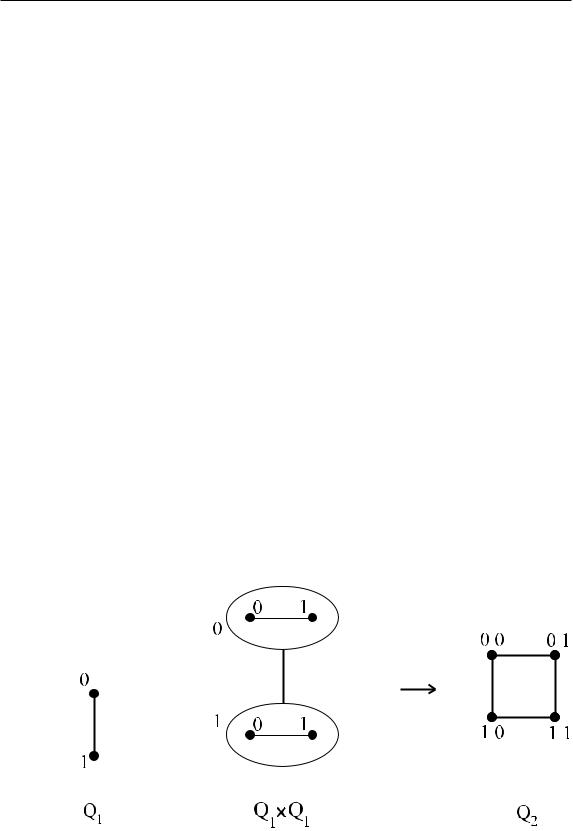
Пример 1.10. Декартово произведение графов используется для задания n-мерных кубов. На рис. 12 изображен одномерный куб Q1 (который получен в результате умножения изолированной вершины на себя) и двумерный куб Q2, который является декартовым произведением
Q1 × Q1.
Ðèñ. 12.
Трехмерный куб (рис. 13) может быть получен последовательным умножением:
Q3 = Q1 × Q1 × Q1 = Q1 × Q2.
15

1.Графы и операции над ними
Ðèñ. 13.
Äëÿ Q4: Q4 = Q1 ×Q1 ×Q1 ×Q1 = Q1 ×Q1 ×Q2 = Q1 ×Q3 = Q2 ×Q2.
На рис. 14. изображена проекция четырехмерного куба на плоскость.
Ðèñ. 14.
Дополнение графа G ãðàô G, множество вершин которого совпадает множеством вершин исходного графа, а множество р¼бер является
16

2.Некоторые специальные виды графов
дополнением множества ребер исходного графа:
G(V, E) G(V, E), E = {(vi, vj) | (vi, vj) / E, i ≠ j}.
Дополнение графа корректно определяется только для простых неориентированных графов.
2.Некоторые специальные виды графов
Для решения конкретных задач, удобно рассматривать частные случаи графов.
Нагруженный граф (орграф) граф (орграф) на множестве ребер которого задана неотрицательная функция w : E(G) → R. Функция w
называется весовой функцией.
Замечание. Нагруженный граф также называют взвешенным.
Регулярный граф степени d простой граф, все вершины которого имеют степень d.
Пустой граф порядка n граф, состоящий из n изолированных вер-
øèí:
On(V, E), V = {v1, v2, ..., vn}, E = .
Простой цикл длины n простой граф, состоящий из n вершин степе-
íè 2:
Cn(V, E), V ={v1, v2, ..., vn},
E ={(v1, v2), (v2, v3), ..., (vn−1, vn), (vn, v1)}.
Паросочетание простой граф, состоящий из 2n висячих вершин:
nK2(V, E), V = {v1, v2, ..., vn, u1, u2, ..., un}, E = {(vi, ui) |1 ≤ i ≤ n}.
Замечание. В одной из последующих глав будет приведено еще одно определение паросочетания, которое никак не противоречит данному здесь, но является более удобным для использования в дальнейшем.
Полный граф порядка n простой граф, состоящий из n вершин степени n − 1:
Kn(V, E), V = {v1, v2, ..., vn}, E = {(vi, vi) | vi V, vj V }.
17
3.Способы матричного задания графов
Замечание. Пустой граф, паросочетание, простой цикл и полный граф являются регулярными графами степени 0, 1, 2 и (n − 1), соответственно.
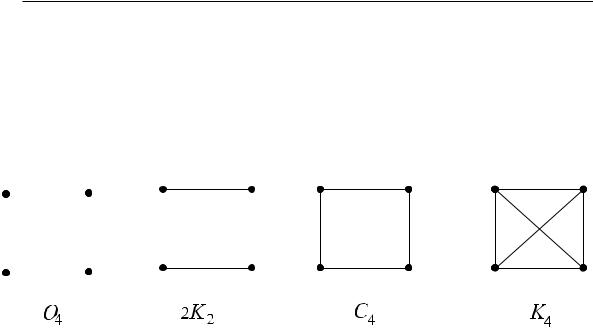
Пример 2.1. На рис. 15 изображены регулярные графы степени 0, 1, 2 и 3 с четырьмя вершинами.
Ðèñ. 15.
3.Способы матричного задания графов
Существует множество способов задания графа. Например, упомянутый ранее рисунок (при этом вершины графа обозначаются точками, а ребра (дуги) линиями (стрелками)), список вершин и ребер, матрица смежности и матрица инцидентности. Кроме того, для некоторых специальных графов (например, двудольных и нагруженных) существуют специальные способы задания. Способ задания выбирается в зависимости от задачи, которую предстоит решать на данном графе.
Матрица смежности. Матрица смежности неориентированного графа G(V, E) квадратная матрица A(G) порядка n (n = |V |), ýëå-
менты которой определяются следующим образом: aij равен числу
ребер, соединяющих вершины vi è vj (при этом петли считаем два-
−→ −→
жды). Матрица смежности ориентированного графа G(V, E ),
−→
квадратная матрица A( G) порядка n (n = |V |), элементы которой определяются следующим образом: aij равен числу дуг, ведущих из
вершины vi в вершину vj (т.е. исходящих из vi и заходящих в vj).
Сумма элементов в строке матрицы смежности орграфа равна полустепени исхода соответствующей вершины, а сумма элементов в столбце полустепени захода. Матрица смежности неориентированного графа симметрична, сумма элементов в i-й строке равна сумме элементов в i-м столб-
це и, соответственно, степени i-й вершины.
18

3.Способы матричного задания графов
Матрица инцидентности. Матрица инцидентности неориентированного графа G(V, E), матрица B(G) порядка n × m (n = |V |, m =
|E|), элементы которой определяются следующим образом: bij = 1,
åñëè vi è ej инцидентны; bij = 0, åñëè vi è ej не инцидентны. Мат-
−→ −→
рица инцидентности ориентированного графа G(V, E ), матрица
−→
B( G) порядка n×m (n = |V |, m = |E|), элементы которой определяются следующим образом: bij = 1, åñëè vi начало дуги ej, bij = −1, åñëè vi конец дуги ej; bij = 0, åñëè vi è ej не инцидентны.
Если граф содержит петли, то значение соответствующего элемента bij выбирается в зависимости от дальнейшего применения этой матрицы. В нашем случае, будем использовать запись bij = 2 для неориентированного графа и запись bij = ±1 для орграфа.
Если ребра графа пронумерованы, то i-й столбец матрицы инцидентности соответствует i-му ребру. Если ребра графа (орграфа) не помечены, то
при составлении матрицы инцидентности будем придерживаться следующего правила: сначала перечисляем ребра (дуги) инцидентные (исходящие из) первой вершины в вершины ее окрестности (в порядке возрастания номеров вершин), затем из второй и т.д. (см. пример 3.1).
Сумма положительных элементов в i-й строке матрицы инцидентности орграфа равна полустепени исхода i-й вершины, а сумма отрицательных
элементов полустепени захода. Для неориентированного графа, сумма элементов в i-й строке равна степени i-й вершины.
Пример 3.1. Для мультиграфа G, изображенного на рис. 16 записать матрицу инцидентности B(G) и матрицу смежности A(G).
1 3 |
|
|
|
|
2 |
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 16. |
|
|
|
|
|
|
|||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
. |
B(G) = |
1 |
1 |
1 |
0 |
0 |
, A(G) = |
0 |
1 |
1 |
1 |
||||
1 |
0 |
0 |
1 |
1 |
1 |
0 |
0 |
2 |
||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
0 |
1 |
0 |
0 |
0 |
|
|
|
1 |
0 |
0 |
0 |
|
|
|
0 |
0 |
1 |
1 |
1 |
|
|
|
1 |
2 |
0 |
0 |
|
19
3.Способы матричного задания графов
Пример 3.2. Для заданного на рис. 17 |
орграфа |
−→ |
||
|
B(→− ) |
|
|
G записать матрицу ин- |
|
и матрицу смежности A |
(−→) |
||
цидентности |
G |
G . |
||
|
|
1 |
3 |
|
|
|
|
|
|
|
2 |
|
|
|
|
|
|
|
|
|
|
|
4 |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||
|
|
|
|
|
|
|
|
Ðèñ. 17. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||
Решение. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
B(−→) = |
1 |
|
1 |
−1 |
|
|
0 |
− |
0 |
|
|
|
(−→) = |
|
0 |
0 |
1 |
1 |
|
|
||||||||
0 |
|
0 |
1 |
|
|
1 |
1 |
|
|
1 |
0 |
0 |
1 |
|
||||||||||||||
G |
|
|
|
|
|
|
|
|
, A G |
|
|
. |
||||||||||||||||
|
1 |
− |
0 |
0 |
− |
0 |
|
|
|
0 |
|
|
0 |
0 |
0 |
0 |
|
|||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|||||||||||||
|
−0 |
|
1 |
0 |
|
|
1 |
|
|
|
1 |
|
|
|
|
0 1 |
0 |
0 |
|
|||||||||
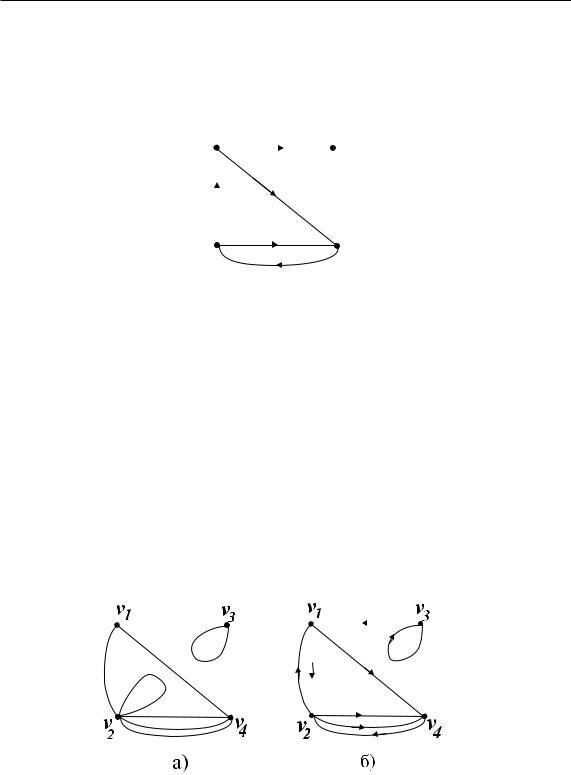
Пример 3.3. Для заданных на рис. 18 |
псевдографов записать матрицы |
|||||||||||||||||||||||||||
смежности и найти степени вершин. |
|
|
|
|
|
|
|
|
|
|
|
|
|
|
||||||||||||||
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Ðèñ. 18. |
Решение. |
|
|
|
|
|
|
|
|
|
|
0 |
2 |
1 |
1 |
|
|
deg(v1) = a1i = 4, deg(v2) = 7, |
|
1 |
3 |
0 |
0 |
|
∑i |
||
à) A(G) = |
|
2 |
2 |
0 |
3 |
|
; |
|
|
|
|
|
|
|
deg(v3) = 3, deg(v4) = 4. |
||
|
|
1 |
0 |
2 |
0 |
|
|
|
|
|
|
|
|
20
