
- •1. Основы алгоритмизации и программирования
- •1.1. Этапы подготовки и решения задач на эвм
- •1.2. Алгоритмы и способы их описания Понятие алгоритма
- •Способы описания алгоритмов
- •Структурные схемы алгоритмов
- •1.3. Компиляция и интерпретация программ
- •1.4. Стили программирования
- •Процедурное программирование
- •Функциональное программирование
- •Логическое программирование
- •Объектно-ориентированное программирование
- •2.1. Пример готовой программы.
- •2.2. Структура основной программы
- •2.3. Алфавит языка
- •2.4. Константы и переменные Константы
- •Переменные
- •Примеры записи имен переменных
- •2.5. Арифметические выражения
- •Примеры вычисления арифметических выражений
- •Стандартные функции
- •Примеры программирования арифметических выражений
- •Контрольные задания
- •1. Составить описания для заданных переменных
- •2.6. Линейные вычислительные процессы
- •Оператор присваивания
- •Странные операторы присваивания
- •Операторы ввода-вывода
- •Операторы ввода исходных данных с клавиатуры
- •Потоковый ввод данных числового типа
- •Форматный ввод
- •Операторы вывода данных на экран Потоковый вывод
- •Форматный вывод
- •Контрольные задания
- •2.7. Разветвляющиеся вычислительные процессы
- •Логические выражения
- •Порядок выполнения операций в логических выражениях
- •Условные операторы
- •Короткий условный оператор
- •Полный условный оператор
- •If (логическое выражение) p1; else p2;
- •Вложенные структуры условных операторов
- •Оператор выбора
- •Контрольные задания
- •2.8. Циклические вычислительные процессы
- •Операторы цикла с условием
- •Оператор цикла do...While
- •Оператор цикла с параметром
- •2.9. Базовые алгоритмы
- •Задача 1. Алгоритм организации счетчика
- •Задача 2. Алгоритм накопления суммы
- •Задача 3. Алгоритм накопления произведения
- •Задача 4. Алгоритм поиска минимального члена последовательности
- •Задача 5. Табулирование функции (или кратные циклы)
- •Задача 6. Вычисление сумм последовательностей
- •2.10. Указатели и массивы Указатели
- •Понятие массива
- •Общий вид описания массива
- •Одномерные массивы
- •Описание одномерного массива
- •Индексированные переменные
- •Ввод-вывод одномерных массивов
- •Обработка одномерных массивов
- •Задача 1. Организация счетчика
- •Задача 2. Накопление суммы и произведения
- •Задача 3. Поиск минимального и максимального элементов массива
- •Двухмерные массивы
- •Описание двухмерного массива
- •Ввод-вывод двухмерного массива
- •Обработка матриц
- •2.11. Подпрограммы Структура сложной программы
- •Функции
- •Общий вид описания функции
- •Обращение к функции
- •Пример программы с функцией
- •Механизм замены параметров
- •Параметры-массивы в функциях
- •Рекурсия
- •Примеры программирования задач с использованием подпрограмм
- •Задача 1
- •2.12. Текстовые данные
- •Символьный тип данных
- •Ввод-вывод символьных данных
- •Обработка символьных данных
- •Ввод-вывод строковых данных
- •Обработка строковых данных
- •Стандартные функции обработки строк
- •Сравнение строк:
- •Сцепление строк
- •Определение длины строки
- •Копирование строк
- •Поиск символа в стоке
- •Пример программы для задачи с текстовыми данными
- •Контрольные задания
- •2.13. Динамическое выделение памяти
- •Структуры данных Понятие структуры
- •Обработка структур
- •Пример задачи с использованием структурированных данных
- •2.15. Файлы данных Понятие файла
- •Работа с файлами
- •Открытие файла
- •Обработка открытого файла
- •Закрытие файла
- •Функции ввода/вывода
- •Работа с текстовыми файлами
- •Обработка бинарных файлов
- •Контрольные задания
- •Заключение
- •Оглавление
Задача 2. Алгоритм накопления суммы
Дана последовательность:
sin 2x, sin 4x, sin 6x, ..., sin l6x
x - заданное вещественное число.
Вычислить сумму членов последовательности, которые по модулю больше 0.3.
Решение
Общий член последовательности имеет вид:
а
=
sin(2nx),
где n
=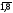 .
.
Для
вычисления суммы в памяти компьютера
выделяется ячейка S,
к содержимому которой прибавляется
член последовательности а
каждый
раз, когда выполняется условие
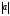 >
0.3. Накопление суммы реализуется
оператором присваиванияS=S+a;.
В начальный момент ячейка для суммирования
должна быть очищена оператором S=0;.
>
0.3. Накопление суммы реализуется
оператором присваиванияS=S+a;.
В начальный момент ячейка для суммирования
должна быть очищена оператором S=0;.
#include "stdafx.h"
#include<math.h>
int main()
{
float a, x, S; //описание переменных задачи
int n;
printf("Введите значение х= ");
scanf("%f",&x);
S=0; //очистка суммы
for(n=1;n<=8;n++) // запуск цикла
{
a=sin(2*n*x);
if ( abs(a)>0.3) S = S + a; /* добавление числа а в сумму, если |a|>0.3 */
}
printf("S=%6.2f",S); // вывод значения суммы на экран
return 0;
}
Задача 3. Алгоритм накопления произведения
Дана последовательность:
cos 0.1, cos 0.2, cos 0.3, ..., cos 10.
Вычислить
значение: Р где
РО
-
произведение отрицательных членов
последовательности.
где
РО
-
произведение отрицательных членов
последовательности.
Решение
Общий член последовательности имеет вид:
y
= cos x, где
0.1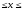 10;Δх
= 0.1.
10;Δх
= 0.1.
Для реализации алгоритма накопления произведения выделяется ячейка памяти РО, в которой осуществляется последовательное перемножение отрицательных членов последовательности с помощью оператора присваивания РО=РО*у; . В начальный момент в ячейку должна быть занесена единица оператором РО=1;.
#include "stdafx.h"
#include<math.h>
int main()
{
float х, у, Р, РО;
РО = 1; // установка нач. значения произведения
for (x=0.1; x<=10; x=x+0.1) //запуск цикла
{
у = cos(x);
if ( y<0) РО = РО*у;
}
Р = fabs(PO);
printf("P=%6.2f",P); //вывод на экран значения P
return 0;
}
Задача 4. Алгоритм поиска минимального члена последовательности
Дана последовательность:
ak=ektg(2k
+ l);
к=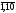 .
.
Найти минимальный член последовательности.
Решение
Для реализации алгоритма выделяется ячейка памяти min, в которую сначала заносится первый член последовательности. Затем, начиная со второго, производится сравнение очередного вычисленного члена последовательности с содержимым ячейки min. Если текущий член последовательности меньше содержимого ячейки min, то oн переписывается в эту ячейку. В противном случае содержимое ячейки min сохраняет прежнее значение. При завершении сравнения всех членов последовательности в ячейке min остается минимальное значение.
Замечание 1. Алгоритм поиска максимального члена последовательности отличается от поиска минимального члена лишь тем, что в ячейке (ей можно дать, например, имя max) запоминается больший из сравниваемых членов последовательности.
Замечание 2. В начальный момент в ячейку min можно занести не первый член последовательности, а достаточно большое число, которое превышало бы область определения сравниваемых чисел (например, min=+1E6;). Тогда при сравнении с содержимым ячейки min первый член последовательности обязательно окажется меньше и перепишется в ячейку min. При поиске максимального члена последовательности в ячейку max в начальный момент заносится, наоборот, достаточно малое число, которое должно быть меньше всех сравниваемых членов последовательности (например, mах= -1Е6;). В этом случае первый из сравниваемых членов последовательности окажется больше содержимого ячейки max и запишется в эту ячейку.
Программа поиска min:
#include "stdafx.h"
#include<math.h>
int main()
{
float a, min;
int k;
min = +1E6; // нач. значение переменной min
for( k=l; k<=10;k++)
{
a = exp(1.0*k)*tan(2*k + 1.0);
if (a<min) min = a; // условие для поиска min
}
printf("min=%6.2f", min);
return 0;
}
