6)Свойства операций над множествами (коммутативность, ассоциативность, дистрибутивность, свойство разности, операции с  и универсумом, …).

Пусть задан универсум U. Тогда A, B, C  U выполняются свойства:

1. Идемпотентность

   A  A = A

   A  A = A

2. Коммутативность

   A  B = B  A

   A  B = B  A

3. Ассоциативность

   A  (B  C) = (A  B)  C

   A  (B  C) = (A  B)  C

4. Дистрибутивность

   A  (B  C) = (A  B)  (A  C)

   A  (B  C) = (A  B)  (A  C)

5. Операции с пустым множеством (свойства нуля)

   A   = A

   A   = 

6. Операции с универсальным множеством (свойства единицы)

   A  U = U

   A  U = A

7. Свойства дополнения

   Инволютивность:

   A A = U A A=

8. Поглощение

   (A  B)  A = A

   (A  B)  A = A

9. Двойственность (законы де Моргана)

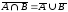
10. Выражение для разности

A \ B = A B

7) Отношения на множествах. Способы задания отношений

N-местным отношением R или N-местным предикатом R на множествах А₁, …, А_n называется любое подмножество прямого произведения А₁ … А_n: R  А₁ … А_n. Элементы a₁, a₂, …, a_n | a_i  A_i при  i = 1, 2, …, n связаны отношением R тогда и только тогда, когда упорядоченный набор (a₁ ,a₂, … a_n)  R.

При N = 1 отношение R является подмножеством множества А₁ и называется унарным отношением или свойством.

Наиболее часто встречается двухместное отношение (N = 2), которое называется бинарным отношением R из множества А в множество В, или соответствием: это подмножество произведения множеств А и В: R  А B.

Если элементы a и b множеств А и В (a,b)R, то говорят, что они находятся в отношении R, для чего часто используется т.н. инфиксная форма записи: aRb. Если R  А A (т.е. А=В), то R называется бинарным отношением на множестве А. Соответственно, отношение R  А ⁿ называется N-местным предикатом на множестве А.

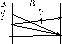
Бинарное отношение можно задать указанием всех пар, для которых это отношение выполняется, или графически. Способы графического представления также могут быть различными. Рассмотрим варианты (см. рис.):

1. Основу графического представления бинарного отношения составляет прямоугольная система координат, где по одной оси отмечаются точки (a), представляющие элементы множества А, а по другой – точки (b), представляющие элементы множества В. Тогда точки с координатами (a,b) обозначают элементы декартова произведения.

2. На той же прямоугольной системе координат отношения для любой пары (a,b) показаны стрелками из a в b.

   

3. Множества A и B показаны точками на параллельных линиях, а отношения между ними – стрелками, направленными от a к b.

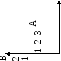
8) Специальные отношения (обратное, универсальное, тождественное). Композиция отношений.

Пусть R есть отношение на множестве A: R  А A, a,b  A. Тогда:

Обратное отношение: R^–1 = {(b,a) | (a,b)  R}.

Дополнение отношения: R = {(a,b) | (a,b)R}.

Тождественное отношение, или диагональ: I_А = {(a,a) | a  A}.

Универсальное (или полное) отношение: U_A = {(a,b) | a  A и b  A}.

Свяжем с каждым бинарным отношением R между множествами A и B два множества – область определения _R и множество (или область) значений _R. Они определяются следующим образом:

_R = {xA| yB | (x,y)R },

_R = {yB| (x,y)R для некоторого xA}.