
- •❶ Электрический заряд. Закон кулона.
- •❷Напряжённость электростатического поля. Принцип суперпозиции. Силовые линии электростатического поля.
- •❸ Потенциал и энергия электростатического поля. Эквипотенциальные поверхности.
- •❺ Связь между энергией и силой Кулона, напряжённостью и потенциалом.
- •❼ Вычисление напряжённости поля вблизи бесконечной плоскости, нити с поверхностной плотностью заряда σ и линейной плотностью заряда τ.
- •❽ Вычисление напряжённости поля вблизи заряженных сферы и шара.
- •❾ Электрическое поле в диэлектриках. Полярные и неполярные диэлектрики.
- •❿ Поляризация диэлектриков. Вектор поляризации. Дипольный электрический момент
- •❶❶ Поток вектора электрического смещения
- •❶❸ Электроёмкость заряженных тел, конденсатора
- •❶❹Энергия заряженных тел, конденсаторов
- •❶❼ Электродвижущая сила. Работа сторонних сил
- •❶❾ Правила Кирхгофа
❺ Связь между энергией и силой Кулона, напряжённостью и потенциалом.
Каждой
точке потенциального поля соответствует,
с одной стороны, некоторое значение
вектора силы , действующей на тело, и, с
другой стороны, некоторое значение
потенциальной энергии . Следовательно,
между силой и потенциальной энергией
должна существовать определенная связь.
Для установления этой связи вычислим элементарную работу ∆A, совершаемую силами поля при малом перемещении ∆S тела, происходящем вдоль произвольно выбранного направления в пространстве, которое обозначим буквой S. Эта работа равна:
![]()
где
![]() -
проекция силы
-
проекция силы
![]() на направление
на направление
![]() .
.
Поскольку
в данном случае работа совершается за
счет запаса потенциальной энергии ∆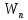 ,
она равна убыли потенциальной энергии
-∆
,
она равна убыли потенциальной энергии
-∆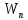 на отрезке оси ∆S:
на отрезке оси ∆S:
∆A
= -∆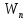
Из
двух последних выражений получаем:
![]()
Откуда:
![]()
Последнее
выражение дает среднее значение
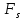 на отрезке ∆S.
Чтобы получить значение
на отрезке ∆S.
Чтобы получить значение
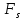 в точке нужно произвести предельный
переход:
в точке нужно произвести предельный
переход:
![]()
Так
как
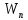 может изменяться не только при перемещении
вдоль оси S,
но также и при перемещениях вдоль других
направлений, предел в этой формуле
представляет собой так называемую
частную производную от
может изменяться не только при перемещении
вдоль оси S,
но также и при перемещениях вдоль других
направлений, предел в этой формуле
представляет собой так называемую
частную производную от
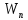 по
S:
по
S:
![]()
Это соотношение справедливо для любого направления в пространстве, в частности и для направлениq декартовых координатных осей х, у, z:
![]()
Эта формула определяет проекции вектора силы на координатные оси. Если известны эти проекции, оказывается определенным и сам вектор силы:
![]()
в
математике вектор
![]() ,
где а - скалярная функция х, у, z, называется
градиентом этого скаляра обозначается
символом
,
где а - скалярная функция х, у, z, называется
градиентом этого скаляра обозначается
символом
![]() .
Следовательно сила равна градиенту
потенциальной энергии, взятого с обратным
знаком:
.
Следовательно сила равна градиенту
потенциальной энергии, взятого с обратным
знаком:
![]()
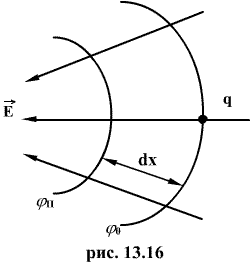
Пусть
положительный заряд q перемещается
силой электрического поля с эквипотенциальной
поверхности, имеющей потенциал , на
близко расположенную эквипотенциальную
поверхность, имеющую потенциал
![]()
Напряженность
поля Е на всем малом пути dx можно считать
постоянной. Тогда работа перемещения
![]() С другой стороны
С другой стороны
![]() . Из этих уравнений получаем
. Из этих уравнений получаем
![]()
Знак минус обусловлен тем, что напряженность поля направлена в сторону убывания потенциала, тогда как градиент потенциала направлен в сторону возрастания потенциала.
❻
Поток вектора
напряжённости электростатического
поля. Теорема Гаусса.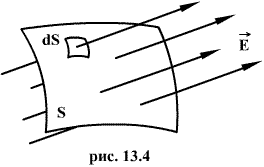
Число линий вектора E, пронизывающих некоторую поверхность S, называется потоком вектора напряженности NE.
Для вычисления потока вектора E необходимо разбить площадь S на элементарные площадки dS, в пределах которых поле будет однородным.
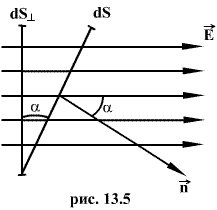
Поток напряженности через такую элементарную площадку будет равен по определению.
![]()
где
![]() - угол между силовой линией и нормалью
- угол между силовой линией и нормалью
![]() к площадке dS;
к площадке dS;
![]() - проекция площадки dS на плоскость,
перпендикулярную силовым линиям. Тогда
поток напряженности поля через всю
поверхность площадки S будет равен
- проекция площадки dS на плоскость,
перпендикулярную силовым линиям. Тогда
поток напряженности поля через всю
поверхность площадки S будет равен
![]()
Так
как
![]() , то:
, то:
![]()
где
![]() - проекция вектора
- проекция вектора
![]() на нормаль и к поверхности dS.
на нормаль и к поверхности dS.
Теорема Гаусса утверждает:
Поток
вектора напряженности электростатического
поля
 через произвольную замкнутую поверхность
равен алгебраической сумме зарядов,
расположенных внутри этой поверхности,
деленной на электрическую постоянную
ε0.
через произвольную замкнутую поверхность
равен алгебраической сумме зарядов,
расположенных внутри этой поверхности,
деленной на электрическую постоянную
ε0.
![]()
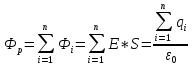

Внешний заряд не создаёт поток.
