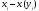Числовые данные

вариант:	6
i	Уi
1	0,77
2	-16,69
3	26,11
4	0,96
5	-205,9
6	56,3
7	-11,05
8	0
9	1,33
10	-39,1
11	1,68
12	-40,88
13	1,88
14	120,5
15	226,85
16	-8,25
17	215,39
18	13,34
19	111,18
20	-8,65
21	-2,49
22	-1,02
23	1,78
24	-163,5
25	69,84
26	-0,1
27	-9,93
28	-61,19
29	-40,52
30	-15,12

Решение:

а) Найдем выборочную ковариацию и выборочный коэффициент корреляции.

По данной выборке 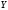построим интервальный ряд, выделив пять частичных интервалов: -207 – -120, -120 – -33, -33 – 54, 54 – 141, 141 – 228. Полученный интервальный статистический ряд запишем в виде таблицы:

	-207 – -120	-120 – -33	-33 – 54	54 – 141	141 – 228
	2	4	18	4	2

Составим корреляционную таблицу для двумерной случайной величины .

		-163,5	-76,5	10,5	97,5	184,5
		-207 – -120	-120 – -33	-33 – 54	54 – 141	141 – 228
-31,5	-40 – -23	2	–	–	–	–	2
-14,5	-23 – -6	–	4	–	–	–	4
2,5	-6 – 11	–	–	18	–	–	18
19,5	11 – 28	–	–	–	4	–	4
36,5	28 – 45	–	–	–	–	2	2
		2	4	18	4	2

Выборочную ковариацию найдем по формуле: .

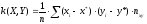(вычислено в задаче №12)

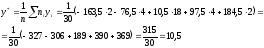
Выборочный коэффициент корреляции найдем по формуле:

б) методом наименьших квадратов оцените параметры модели X=aY+b, протестируйте гипотезу {a=0};

в) методом наименьших квадратов оцените параметры модели Y=kX+d, протестируйте гипотезу {k=0};

г) в пунктах (б), (в) найдите и сравните коэффициенты R²;

д) в пунктах (б), (в) протестируйте близость эмпирического распределения остатков моделей к нормальному;

е) каково ожидаемое значение с.в. Y, если известно значение с.в. X? Каков доверительный интервал для Y в этом случае? Постройте график этих  зависимостей для выборочных значений X_i и сравните с выборочными значениями Y_i.

б) Методом наименьших квадратов оценим параметры модели X=aY+b. а=0.2, b=-0.03.

в) Методом наименьших квадратов оценим параметры модели Y=kX+d. k=5.09, d=0.02.

г) R — коэффициент детерминации; это доля объяснённой дисперсии отклонений зависимой переменной от её среднего значения. .

При оценке модели регрессии X на Y получаем ; значит, почти 100% доля признакаY объясняется признаком Х. Аналогично получаем .

Остатки модели:

i	Уi	Xi
1	0,77	0,15	0,7821	0,124	-0,0121	0,026
2	-16,69	-3,28	-16,6766	-3,368	-0,0134	0,088
3	26,11	5,13	26,1303	5,192	-0,0203	-0,062
4	0,96	0,19	0,9857	0,162	-0,0257	0,028
5	-205,9	-40,44	-205,821	-41,21	-0,079	0,77
6	56,3	11,06	56,314	11,23	-0,014	-0,17
7	-11,05	-2,17	-11,0267	-2,24	-0,0233	0,07
8	0	0	0,0186	-0,03	-0,0186	0,03
9	1,33	0,26	1,342	0,236	-0,012	0,024
10	-39,1	-7,68	-39,0726	-7,85	-0,0274	0,17
11	1,68	0,33	1,6983	0,306	-0,0183	0,024
12	-40,88	-8,03	-40,8541	-8,206	-0,0259	0,176
13	1,88	0,37	1,9019	0,346	-0,0219	0,024
14	120,5	23,67	120,4989	24,07	0,0011	-0,4
15	226,85	44,56	226,829	45,34	0,021	-0,78
16	-8,25	-1,62	-8,2272	-1,68	-0,0228	0,06
17	215,39	42,31	215,3765	43,048	0,0135	-0,738
18	13,34	2,62	13,3544	2,638	-0,0144	-0,018
19	111,18	21,84	111,1842	22,206	-0,0042	-0,366
20	-8,65	-1,7	-8,6344	-1,76	-0,0156	0,06
21	-2,49	-0,49	-2,4755	-0,528	-0,0145	0,038
22	-1,02	-0,2	-0,9994	-0,234	-0,0206	0,034
23	1,78	0,35	1,8001	0,326	-0,0201	0,024
24	-163,5	-32,11	-163,421	-32,73	-0,0787	0,62
25	69,84	13,72	69,8534	13,938	-0,0134	-0,218
26	-0,1	-0,02	-0,0832	-0,05	-0,0168	0,03
27	-9,93	-1,95	-9,9069	-2,016	-0,0231	0,066
28	-61,19	-12,02	-61,1632	-12,268	-0,0268	0,248
29	-40,52	-7,96	-40,4978	-8,134	-0,0222	0,174
30	-15,12	-2,97	-15,0987	-3,054	-0,0213	0,084

Протестируем принадлежность остатка модели регрессии Y=kX+d, k=5.09, d=0.02 к нормальному распределению. Будем использовать критерий Пирсона. Для этого разобьём область (-0.08, 0.022) на 5 интервалов с границами -0.08, -0.025, -0.021, -0.017, -0.013, 0.022 и подсчитаем число элементов выборки, попавших в каждый интервал. Вычислим гипотетическую вероятность попадания в эти же интервалы случайной величиныZ~N(0,0.02) (распределение остатков модели должно иметь математическое ожидание 0; дисперсия вычислена по выборке).

номер	середина	частота	теор.частота
1	-0.0525	6	11.74
2	-0.023	6	2.42
3	-0.019	5	1.52
4	-0.015	7	2.38
5	0.0045	6	10.48

По таблице можно заключить, даже не вычисляя реализацию статистики , что эмпирическая (выборочная) частоты слишком отличаются, чтобы принадлежать одному распределению. Всё же вычислим её: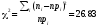. Это значение соответствует очень малому уровню значимости(меньше 0.01), поэтому гипотезу следует отвергнуть.

Протестируем принадлежность остатка модели регрессии X=aY+b. а=0.2, b=-0.03 к нормальному распределению. Будем использовать критерий Пирсона. Для этого разобьём область (-0.8, 0.8) на 5 интервалов с границами -0.8, -0.2, 0.025, 0.05, 0.1, 0.8 и подсчитаем число элементов выборки, попавших в каждый интервал. Вычислим гипотетическую вероятность попадания в эти же интервалы случайной величиныZ~N(0,0.305) (распределение остатков модели должно иметь математическое ожидание 0; дисперсия вычислена по выборке).

номер	середина	частота	теор.частота
1	-0.5	5	7.54
2	-0.0875	7	8.30
3	0.0375	6	0.97
4	0.075	6	1.90
5	0.45	6	11.01

, поэтому гипотезу о принадлежности остатков модели к нормальному распределению следует отвергнуть.

Построим доверительный интервал для математического ожидания величины Y следующим образом:

,

где – стандартная ошибка групповой средней,,– выборочная остаточная дисперсия (дисперсия остатка модели); статистикаприпримет значение 2.05. Таким образом,

или .

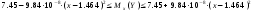Построим график зависимости ожидаемых значений Y при известных значениях Х.

Как и следовало ожидать (судя по величине остатков моделей), графики на рисунке выше неразличимы.