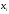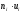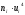Часть II: Математическая статистика (практикум)
Задание 1.
По данной выборке Xi выполните следующие вычисления:
а) постройте гистограмму, полигон, выборочную функцию распределения;
б) вычислите выборочные моменты и связанные величины (первый, второй, третий, дисперсию, СКО, эксцесс и коэффициент асимметрии);
в) оцените методом моментов или/и методом максимального правдоподобия по выборке параметры основных непрерывных распределений (равномерное, экспоненциальное, нормальное и пр.), оцените близость оценок теоретических распределений к выборочному; подберите качественное описание выборочного распределения теоретическим;
г) предположив, что выборка получена из нормального распределения, протестируйте гипотезы равенства среднего нулю при неизвестной дисперсии; равенства среднего нулю при дисперсии, равной выборочной;
Числовые данные
|
вариант: |
6 |
|
i |
Xi |
|
1 |
0,15 |
|
2 |
-3,28 |
|
3 |
5,13 |
|
4 |
0,19 |
|
5 |
-40,44 |
|
6 |
11,06 |
|
7 |
-2,17 |
|
8 |
0 |
|
9 |
0,26 |
|
10 |
-7,68 |
|
11 |
0,33 |
|
12 |
-8,03 |
|
13 |
0,37 |
|
14 |
23,67 |
|
15 |
44,56 |
|
16 |
-1,62 |
|
17 |
42,31 |
|
18 |
2,62 |
|
19 |
21,84 |
|
20 |
-1,7 |
|
21 |
-0,49 |
|
22 |
-0,2 |
|
23 |
0,35 |
|
24 |
-32,11 |
|
25 |
13,72 |
|
26 |
-0,02 |
|
27 |
-1,95 |
|
28 |
-12,02 |
|
29 |
-7,96 |
|
30 |
-2,97 |
Решение:
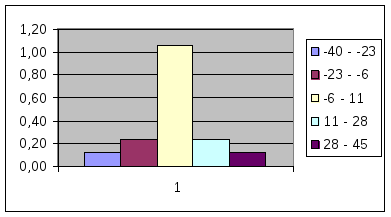
а) Построим гистограмму, полигон, выборочную функцию распределения.
По
данной выборке построим интервальный
вариационный ряд, выделив пять частичных
интервалов: -40 – -23, -23 – -6, -6 – 11, 11 – 28,
28 – 45. Длина частичных интервалов
 .
Полученный интервальный статистический
ряд запишем в виде таблицы:
.
Полученный интервальный статистический
ряд запишем в виде таблицы:
|
|
-40 – -23 |
-23 – -6 |
-6 – 11 |
11 – 28 |
28 – 45 |
|
|
2 |
4 |
18 |
4 |
2 |
Найдем плотность частоты и запишем в таблицу:
|
|
-40 – -23 |
-23 – -6 |
-6 – 11 |
11 – 28 |
28 – 45 |
|
|
2 |
4 |
18 |
4 |
2 |
|
|
|
|
|
|
|
Построим полигон и гистограмму:

Из интервального ряда составим вариационный ряд, выбрав в качестве вариант середины интервалов. Запишем полученный ряд в виде таблицы:
|
|
-31,5 |
-14,5 |
2,5 |
19,5 |
36,5 |
|
|
2 |
4 |
18 |
4 |
2 |
Построим
выборочную функцию распределения
 ,
учитывая, что объем выборки
,
учитывая, что объем выборки .
.
Значения
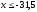 наблюдались 0 раз; следовательно,
наблюдались 0 раз; следовательно, при
при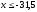 .
.
Значения
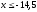 наблюдались 2 раза; следовательно,
наблюдались 2 раза; следовательно, при
при .
Значения
.
Значения наблюдались 6 раз; следовательно,
наблюдались 6 раз; следовательно, при
при .
.
Значения
 наблюдались 24 раза; следовательно,
наблюдались 24 раза; следовательно, при
при .
Значения
.
Значения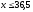 наблюдались 28 раз; следовательно,
наблюдались 28 раз; следовательно, при
при .
.
Значения
 наблюдались 30 раз; следовательно,
наблюдались 30 раз; следовательно, при
при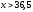 .
.
Выборочная
функция распределения
 имеет вид:
имеет вид:
 .
.
б) Вычислим выборочные моменты и связанные величины (первый, второй, третий, дисперсию, СКО, эксцесс и коэффициент асимметрии). Воспользуемся методом произведений, для чего составим расчетную таблицу: варианты записываем в первый столбец; частоты – во второй, сумму частот поместим в нижнюю клетку столбца
|
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
|
|
|
|
|
|
|
|
-31,5 |
2 |
-2 |
-4 |
8 |
-16 |
32 |
|
-14,5 |
4 |
-1 |
-4 |
4 |
-4 |
4 |
|
2,5 |
18 |
0 |
0 |
0 |
0 |
0 |
|
19,5 |
4 |
1 |
4 |
4 |
4 |
4 |
|
36,5 |
2 |
2 |
4 |
8 |
16 |
32 |
|
|
|
|
|
|
|
|
В качестве ложного нуля С выберем варианту 2,5. В клетке третьего столбца, которая принадлежит строке, содержащей выбранный ложный нуль, пишем 0; над нулем последовательно записываем –1; -2, а под нулем – 1; 2.
Выборочные
условные моменты
 -го
порядка определим по формуле
-го
порядка определим по формуле
 ;
;
 ;
; ;
; .
.
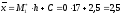 ;
;
 ;
;
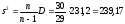 ;
;

Найдем центральные эмпирические моменты 3-го и 4-го порядка:
 ;
;
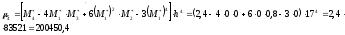
Найдем значения коэффициента асимметрии и эксцесс по соответствующим формулам:
 ;
;

в) оцените методом моментов или/и методом максимального правдоподобия по выборке параметры основных непрерывных распределений (равномерное, экспоненциальное, нормальное и пр.), оцените близость оценок теоретических распределений к выборочному; подберите качественное описание выборочного распределения теоретическим.
|
i |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 | |
|
Xi |
0,15 |
-3,28 |
5,13 |
0,19 |
-40,44 |
11,06 |
-2,17 |
0 |
0,26 | |
|
10 |
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 | |
|
-7,68 |
0,33 |
-8,03 |
0,37 |
23,67 |
44,56 |
-1,62 |
42,31 |
2,62 |
21,84 | |
|
20 |
21 |
22 |
23 |
24 |
25 |
26 |
27 |
28 |
29 |
30 |
|
-1,7 |
-0,49 |
-0,2 |
0,35 |
-32,11 |
13,72 |
-0,02 |
-1,95 |
-12,02 |
-7,96 |
-2,97 |
экспоненциальное распределение: X~Exp(
 ),
), .
.
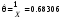 .
.
нормальное распределение: X~
 . Параметр
. Параметр состоит из двух компонент:
состоит из двух компонент: .
.
 ,
,
 .
.
равномерное распределение: X~R(a, b); q=(a, b).
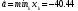 ,
,
 .
.
гамма — распределение: X~
 ,
(λ>0,
,
(λ>0,
 )
.
)
. .
Оценки получаются из решения системы:
.
Оценки получаются из решения системы:

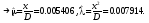
Визуально
можно определить, что лучше всего
подходит нормальное распределение.
г)
Предположив, что выборка получена из
нормального распределения, протестируем
гипотезы равенства среднего нулю при
неизвестной дисперсии; равенства
среднего нулю при дисперсии, равной
выборочной. При проверке гипотез будем
использовать уровень значимости
 .
.
Протестируем
гипотезы равенства среднего нулю при
известной дисперсии. Предположим, что
дисперсия известна и равна выборочной
дисперсии. Выборочное среднее
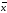 и выборочная дисперсия
и выборочная дисперсия были вычислены в пункте б) данной задачи:
были вычислены в пункте б) данной задачи: ,
, .
Среднее квадратическое отклонение
.
Среднее квадратическое отклонение .
.
Проверим
нулевую гипотезу
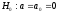 при конкурирующей гипотезе
при конкурирующей гипотезе .
.
Найдем
наблюдаемое значение критерия
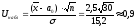 .
.
По
условию, конкурирующая гипотеза имеет
вид
 ,
поэтому критическая область –
двусторонняя. Найдем критическую точку
из равенства
,
поэтому критическая область –
двусторонняя. Найдем критическую точку
из равенства
 .
По таблице значений функции Лапласа
находим
.
По таблице значений функции Лапласа
находим
 .
.
Так
как
 -
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
-
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
Проверим
нулевую гипотезу
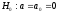 при конкурирующей гипотезе
при конкурирующей гипотезе .
Найдем критическую точку из равенства
.
Найдем критическую точку из равенства
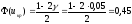 .
По таблице значений функции Лапласа
находим
.
По таблице значений функции Лапласа
находим
 .
.
Так
как
 -
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
-
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
Проверим
нулевую гипотезу
 при конкурирующей гипотезе
при конкурирующей гипотезе .
Найдем критическую точку из равенства
.
Найдем критическую точку из равенства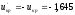 .
.
Так
как
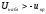 -
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
-
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
Протестируем
гипотезы равенства среднего нулю при
неизвестной дисперсии. Выборочное
среднее
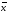 и исправленное среднее квадратическое
и исправленное среднее квадратическое были вычислены в пункте б) данной задачи:
были вычислены в пункте б) данной задачи: ,
, .
.
Проверим
нулевую гипотезу
 при конкурирующей гипотезе
при конкурирующей гипотезе .
.
Найдем
наблюдаемое значение критерия
 .
.
По
условию, конкурирующая гипотеза имеет
вид
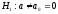 ,
поэтому критическая область –
двусторонняя. По таблице распределения
Стьюдента по уровню значимости
,
поэтому критическая область –
двусторонняя. По таблице распределения
Стьюдента по уровню значимости и числу степеней свободы
и числу степеней свободы находим
находим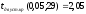 .
.
Так
как
 -
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
-
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
Проверим
нулевую гипотезу
 при конкурирующей гипотезе
при конкурирующей гипотезе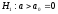 .
Найдем
.
Найдем .
.
Так
как
 -
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
-
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
Проверим
нулевую гипотезу
 при конкурирующей гипотезе
при конкурирующей гипотезе .
Найдем критическую точку из равенства
.
Найдем критическую точку из равенства .
.
Так
как
 -
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
-
нет оснований отвергнуть нулевую
гипотезу. Другими словами, выборочная
и гипотетическая средние различаются
незначительно.
Задание 2.
По выборкам Xi, Yi выполните следующие вычисления:
а) найдите выборочную ковариацию и выборочный коэффициент корреляции;
б) методом наименьших квадратов оцените параметры модели X=aY+b, протестируйте гипотезу {a=0};
в) методом наименьших квадратов оцените параметры модели Y=kX+d, протестируйте гипотезу {k=0};
г) в пунктах (б), (в) найдите и сравните коэффициенты R2;
д) в пунктах (б), (в) протестируйте близость эмпирического распределения остатков моделей к нормальному;
е) каково ожидаемое значение с.в. Y, если известно значение с.в. X? Каков доверительный интервал для Y в этом случае? Постройте график этих зависимостей для выборочных значений Xi и сравните с выборочными значениями Yi.