Числовые данные

i1=-0,036;

i2=-0,809;

i3=0,315;

i4=-0,265;

i5=0,471;

i6=-0,386;

i7=0,576;

i8=-0,556;

i9=0,508;

i10=0,477;

K=3

Решение

а) найдите оценку параметра A методом моментов, если известно, что выборка сделана из равномерного распределения U(–1;A)

Решение. Известно, что для равномерно распределенной на отрезке случайной величины математическое ожидание может быть вычислено по формуле. Точеной оценкой математического ожидания является среднее арифметическое.

В нашем случае имеем .

б) найдите оценку методом моментов параметра B, если известно, что выборка сделана из равномерного распределения U(-B;B).

Решение. Известно, что для равномерно распределенной на отрезке случайной величины дисперсия может быть вычислено по формуле. Точеной оценкой дисперсии является выборочная дисперсия.

В нашем случае имеем

в) найдите оценки методом максимального правдоподобия параметров c и C, если известно, что выборка сделана из равномерного распределения U(c; C);

Решение.

Запишем функцию плотности вероятностей

.

Пусть , тогда

Составим функцию правдоподобия:

если ,, …,, т.е, то

.

Если , то, поскольку в этом случае хотя бы один из сомножителейуказанного произведения обращается в нуль.

График функции правдоподобия при оценке параметра равномерного распределения имеет вид

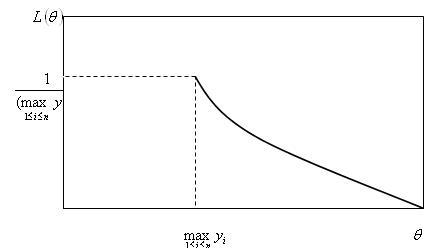
Наибольшее значение функции правдоподобия находиться в точке , т.е..

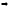
г) найдите (и сравните) оценки параметра L методом моментов и методом максимального правдоподобия, если известно, что выборка сделана из экспоненциального E_L распределения;

Решение. Пусть наблюдаемая в эксперименте случайная величина имеет экспоненциальное распределение с плотностью

Применяя метод максимального правдоподобия, найдем точечную оценку для параметра .

Составим функцию правдоподобия

.

Применяя операцию логарифмирования, получаем

.

Следовательно, уравнение правдоподобия имеет вид

.

Применяя метод моментов, найдем точечную оценку для параметра .

Найдем математическое ожидание случайной величины, имеющей экспоненциальное распределение:

Так как точеной оценкой математического ожидания является среднее арифметическое , то получаем.

Применяя два различных метода, мы получили один и тот же результат

д) найдите оценку параметра m методом моментов, если известно, что выборка сделана из нормального распределения N(m, 1).

Решение. Пусть непрерывная случайная величина распределена по нормальному закону с параметрами и.

Тогда плотность вероятности имеет вид

.

Найдем математическое ожидание случайной величины :

.

Первый интеграл равен нулю как интеграл от нечетной функции по симметричному относительно начала координат промежутку, второй интеграл - интеграл Эйлера-Пуассона.

Так как точеной оценкой математического ожидания является среднее арифметическое , то получаем

е) найдите оценки параметров M и S любым известным методом, если известно, что выборка сделана из нормального распределения N(M, S);

Решение. Пусть непрерывная случайная величина распределена по нормальному закону с параметрами и.

Тогда плотность вероятности имеет вид

.

Найдем математическое ожидание случайной величины :

.

Первый интеграл равен нулю как интеграл от нечетной функции по симметричному относительно начала координат промежутку, второй интеграл - интеграл Эйлера-Пуассона.

Так как точеной оценкой математического ожидания является среднее арифметическое , то получаем

Найдем дисперсию случайной величины :

.

Точеной оценкой дисперсии является выборочная дисперсия .

Поэтому

ж) постройте гистограмму и полигон по выборке, количество интервалов — 3;

Найдем максимальное и минимальное значения по выборке:

, .

Размах варьирования .

Рассмотрим три равных частичных интервала, в которые попадают все элементы выборки

	[-0,81;-0,34]	[-0,34;0,13]	[0,13;0,6]
	3	2	5

з) в каждом из пунктов (а) — (е) оцените близость данного теоретического распределения к эмпирическому на основе критерия Пирсона; какое из распределений (а) — (е) лучше описывает выборку?

Решение.

	[-0,81;-0,41]	[-0,41;-0,01]	[-0,01;0,39]	[0,39;0,79]
	2	3	1	4

_{В пункте а) была найдена оценка параметра .}

_{Найдем плотность предполагаемого равномерного распределения на отрезке}

,

Найдем теоретические частоты:

,

,

,

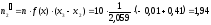Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	2	1,94	0,06	0,0036	0,0019
[-0,41;-0,01]	3	1,94	1,06	1,1236	0,5792
[-0,01;0,39]	1	1,94	-0,94	0,8836	0,4555
[0,39;0,79]	4	1,94	2,06	4,2436	2,1874
сумма	10

Найдем по таблице критических точек распределения по уровню значимостии числу степеней свободыкритическую точку правосторонней критической области.

Так как наблюдаемое значение критерия меньше критического значения критерия (3,224<3,8), то делаем вывод о том, что наблюдения согласуются с равномерным распределением на рассматриваемом отрезке на уровне значимости .

_{В пункте б) была найдена оценка параметра .}

_{Найдем плотность предполагаемого равномерного распределения на отрезке}

,

Найдем теоретические частоты:

,

,

,

Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	2	2,4	-0,4	0,16	0,0667
[-0,41;-0,01]	3	2,4	0,6	0,36	0,15
[-0,01;0,39]	1	2,4	-1,4	1,96	0,8167
[0,39;0,79]	4	2,4	1,6	2,56	1,0667
сумма	10

Найдем по таблице критических точек распределения по уровню значимостии числу степеней свободыкритическую точку правосторонней критической области.

Так как наблюдаемое значение критерия меньше критического значения критерия (2,1001<3,8), то делаем вывод о том, что наблюдения согласуются с равномерным распределением на рассматриваемом отрезке на уровне значимости .

_{В пункте} u) была найдена оценка параметра _.

_{Найдем плотность предполагаемого экспоненциального распределения} ,

Найдем теоретические частоты:

,

,

,

Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	2	8419603071104	-8419603071102	8419603071100
[-0,41;-0,01]	3	10870723	-10870720	10870715
[-0,01;0,39]	1	474,6	-473,6	472,6
[0,39;0,79]	4	0,0007	3б9993	22849,14
сумма	10

Найдем по таблице критических точек распределения по уровню значимостии числу степеней свободыкритическую точку правосторонней критической области.

Так как наблюдаемое значение критерия значительно больше критического значения критерия , то делаем вывод о том, что наблюдения не согласуются с экспоненциальным распределением на уровне значимости .

_{В пункте д) была найдена оценка параметра .}

_{Найдем плотность предполагаемого нормального распределения с парметрами 0,0295 и 1}

,

Найдем теоретические частоты:

,

,

,

Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	1	1,295	-0,295	0,16	0,067
[-0,41;-0,01]	3	1,54	1,46	2,1316	1,38
[-0,01;0,39]	1	1,57	-0,57	0,3249	0,21
[0,39;0,79]	4	1,36	2,64	6,9696	5,12
сумма	10

Найдем по таблице критических точек распределения по уровню значимостии числу степеней свободыкритическую точку правосторонней критической области.

Так как наблюдаемое значение критерия больше критического значения критерия , то делаем вывод о том, что наблюдения не согласуются с нормальным распределением с параметрами 0, 0295 и 1 на уровне значимости .

_{В пункте е) была найдена оценка параметра ,}

_{Найдем плотность предполагаемого нормального распределения с парметрами 0,0295 и 0,48}

,

Найдем теоретические частоты:

,

,

,

Сравним эмпирические и теоретические частоты, используя критерий Пирсона

[-0,81;-0,41]	1	1,39	-0,39	0,1521	0,109
[-0,41;-0,01]	3	2,89	0,11	0,0121	0,004
[-0,01;0,39]	1	3,05	-2,05	4,2025	1,378
[0,39;0,79]	4	1,7	2,3	5,29	3,112
сумма	10

Найдем по таблице критических точек распределения по уровню значимостии числу степеней свободыкритическую точку правосторонней критической области.

Так как наблюдаемое значение критерия больше критического значения критерия , то делаем вывод о том, что наблюдения не согласуются с нормальным распределением с параметрами 0, 0295 и 0,48 на уровне значимости .

_{Из представленных распределений указанная выборка лучше всего согласуется с равномерным распределением на отрезке , т.к. в этом случае получено наименьшее наблюдаемое значение критерия.}