Контрольная работа

Министерство Российской Федерации по связи и информатизации

Сибирский Государственный Университет Телекоммуникаций и Информатики

Межрегиональный центр переподготовки специалистов

Контрольная работ

по предмету

«Методы оптимальных решений»

Вариант № 1

Выполнил: слушатель

Проверил: преподаватель Галкина М.Ю.

2012

Задача №1.Между двумя пунктами, расстояние между которыми равно 1000 км, необходимо с наименьшими затратами осуществить связь, имеющую 9 телефонных, 13 телеграфных и c фототелеграфных каналов 16 помощью кабелей двух типов. Кабель первого типа содержит 4 телефонных, 3 телеграфных и 2 фототелеграфных каналов, а кабель второго типа – 1 телефонных, 2 телеграфных и 5 фототелеграфных каналов. Стоимость 1 км кабеля первого типа равна 5 тыс.руб., второго типа – 1 тыс.руб_..

Номер варианта	а	b	с	а1	b1	с1	а2	b2	с2	p1	p2
1	9	13	16	4	3	2	1	2	5	5	1

Пусть x₁ – количество кабелей первого типа, x₂ – количество кабелей второго типа; очевидно, x₁, x₂ – целые, . Тогда количество телефонных каналов равно 4x₁ + x₂, телеграфных – 3x₁ + 2x₂ и фототелеграфных – 2x₁ + 5x₂. Для осуществления связи необходимо наличие не менее требуемого числа каналов. Затраты на осуществление связи – 5000x₁ + 1000x₂.

Получаем следующую математическую модель:

Решение. Решим задачу графическим методом

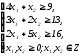
Первое неравенство системы ограничений задачиописывает полуплоскость, лежащую выше прямой , которую строим по точкам (1;5) и (2;1).

Второе неравенство системы ограничений задачиописывает полуплоскость, лежащую выше прямой , которую строим по точкам (1;5) и (3;2).

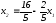Третье неравенство системы ограничений задачиописывает полуплоскость, лежащую выше прямой , которую строим по точкам (3;2) и (5;6/5).

Неограниченная сверху область ABCD - множество допустимых решений системы ограничений задачи.

Строим линию уровня 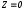, т.е.

Строим вектор нормали , координаты которого пропорциональны коэффициентам при соответствующих переменных в функции цели.

Перемещая линию уровня против направления нормали, видим, что опорное положение прямая принимает в точке А(0;9). Поэтому , .

Задача2 Составить двойственную задачу к задаче 1. Найти ее решение по теореме равновесия. 

Решение. Составим двойственную задачу к данной

.

Найдем оптимальное решение двойственной задачи по теореме равновесия. Запишем условия дополняющей нежесткости

Подставим в составленную систему оптимальное решение исходной задачи :

Тогда

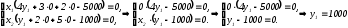
Оптимальное решение двойственной задачи

Задача3 Решить двухкритериальную задачу линейного программирования методом идеальной точки.

Решение.

OABCD – область допустимых решений системы ограничений задачи.

Рассмотрим преобразование

В этом случае,

,, , ,

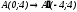Точка утопии М*(3,4) – точка, в которой первая и вторая координаты новых точек принимают максимальные значения.

Граница Парето пятиугольника О` A`B`C`D` состоит из отрезков O`A` и O`D`.

Найдем уравнение прямой, проходящей через точки и :

.

Найдем уравнение прямой L, перпендикулярной прямой O`A` и проходящей через точку М:

.

Таким образом, уравнение искомой прямой имеет вид:.

Найдем точку пересечения полученных перпендикулярных прямых, решив систему из соответствующих уравнений:

Находим соответствующие значения x и y: